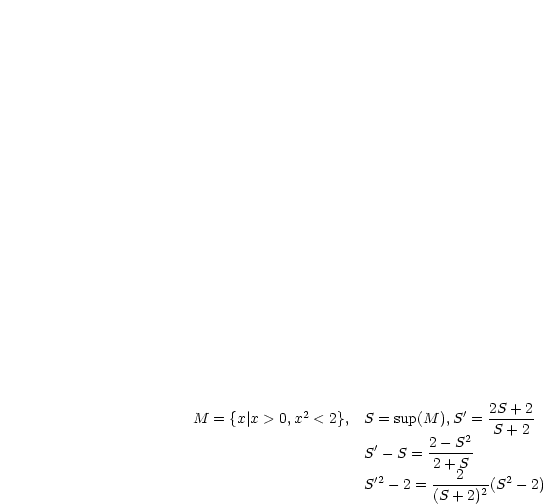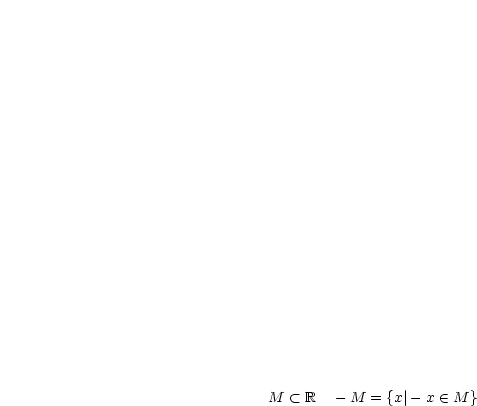
|
|

Es sei  .
.  heißt obere Grenze/Supremum von
heißt obere Grenze/Supremum von  , falls
, falls  kleinste
obere Schranke von
kleinste
obere Schranke von  ist.
ist.


 , folgt
, folgt 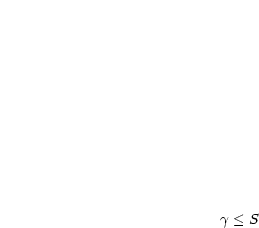
Für die untere Grenze/Infimum gilt:  . . |

 gibt die größte untere Schranke von
gibt die größte untere Schranke von  an.
an.


 folgt wiederum, daß
folgt wiederum, daß  .
.
Zeige, daß folgende Ungleichung gilt:

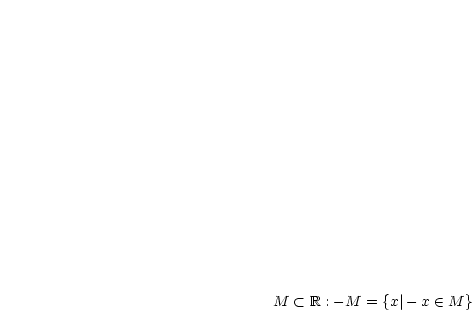
 sei untere Schranke.
sei untere Schranke.  bedeutet dann, daß
bedeutet dann, daß 

 .
.
Betrachten wir folgende Menge:

Die Behauptung ist nun, daß  gilt.
gilt.
Unser Ziel ist es nun, die obere Schranke so zu wählen, daß  gilt. Dazu
nehmen wir folgendes an:
gilt. Dazu
nehmen wir folgendes an:

Das geht nicht, da 

 , was hier somit nicht erfüllt wäre. Es handelt
sich also um einen Widerspruch und somit gilt
, was hier somit nicht erfüllt wäre. Es handelt
sich also um einen Widerspruch und somit gilt  .
.
|
Für das Supremum (kleinste obere Schranke) einer Menge gilt folgendes:
Für das Infimum (größte untere Schranke) wiederum folgt:
|
Besitzt  ein Maximum, dann gilt:
ein Maximum, dann gilt: 
 ist nicht
nach oben beschränkt, d.h. zu jeder Zahl
ist nicht
nach oben beschränkt, d.h. zu jeder Zahl  gibt es
gibt es  mit
mit  .
Wenn
.
Wenn  nicht nach unten beschränkt ist, gibt es zu jeder Zahl
nicht nach unten beschränkt ist, gibt es zu jeder Zahl  ein
ein
 mit
mit  . Ist
. Ist  nicht nach oben beschränkt, so schreiben wir
nicht nach oben beschränkt, so schreiben wir
 . Ist
. Ist  nicht nach unten beschränkt, so schreiben wir
nicht nach unten beschränkt, so schreiben wir
 .
.
 sei nicht nach unten beschränkt:
sei nicht nach unten beschränkt: 
 ist nicht nach oben beschränkt:
ist nicht nach oben beschränkt: 

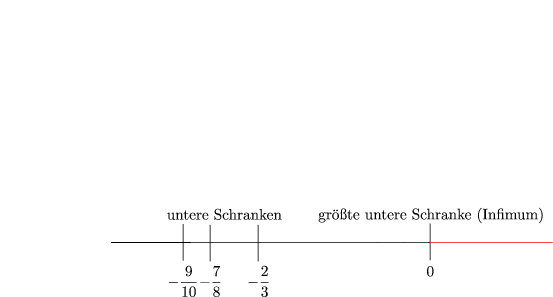
Es ist bekannt, daß 

 , somit stellt 0 eine untere
Schranke dar. 0 ist sogar die größte untere Schranke (Infimum). Des weiteren ist
, somit stellt 0 eine untere
Schranke dar. 0 ist sogar die größte untere Schranke (Infimum). Des weiteren ist


 . Folglich ist 0 kein Minimum anders als bei
. Folglich ist 0 kein Minimum anders als bei 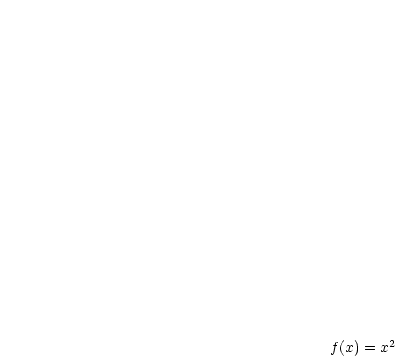 .
Dort ist 0 nämlich gleichzeitig größte untere Schranke und Minimum, da
.
Dort ist 0 nämlich gleichzeitig größte untere Schranke und Minimum, da
 .
.
 :
: sind Zeichen (keine Zahlen!), mit denen formal wie folgt gerechnet wird:
sind Zeichen (keine Zahlen!), mit denen formal wie folgt gerechnet wird:




Folgende Ausdrücke besitzen keinen definierten Wert. Der Wert hängt vom mathematischen Zusammenhang ab (unbestimmte Ausdrücke):


| Jede nichtleere Menge reeller Zahlen, die nach oben beschränkt ist, besitzt ein Supremum. |

Für  ist dies falsch!
ist dies falsch!
Die Menge  ist nicht nach oben beschränkt. ist nicht nach oben beschränkt. |
 . Wir zeigen dies indirekt. Wir nehmen an, es gelte:
. Wir zeigen dies indirekt. Wir nehmen an, es gelte:  für ein
für ein  .
Dann folgt daraus, daß
.
Dann folgt daraus, daß  existiert. Dann gilt:
existiert. Dann gilt:

Mit  und mit
und mit  gelte
gelte 

 . Dann folgt hieraus
wiederum:
. Dann folgt hieraus
wiederum:

Dabei handelt es sich also um einen Widerspruch:  ist unbeschränkt.
ist unbeschränkt.
Zu jeder reellen Zahl  gibt es gibt es  mit mit    . . |
Zu jeder positiven Zahl  gibt es eine natürliche Zahl gibt es eine natürliche Zahl  mit: mit: |
    |
 |
Es gelte für 
Für  , , gelten: gelten:  und und  . Dann gibt es . Dann gibt es  mit mit 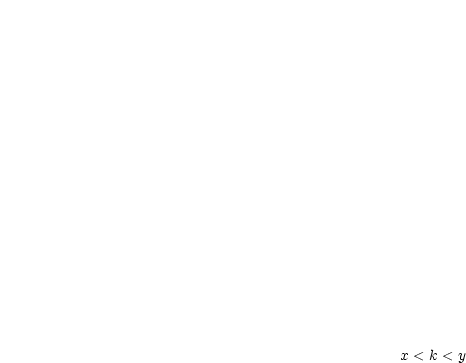 . . |
Für  gelte gelte  . Dann gibt es ein . Dann gibt es ein  mit mit  . Die Dichtheit der rationalen Zahlen in . Die Dichtheit der rationalen Zahlen in  : : |
Für  : :  |


Zu  ,
,  mit
mit  gibt es
gibt es  mit
mit  .
.




Wäre  , so würde folgen:
, so würde folgen:  . Dabei handelt es sich um einen
Widerspruch.
. Dabei handelt es sich um einen
Widerspruch.
 genügt (V) nicht. Das heißt: genügt (V) nicht. Das heißt: |
Aus  , ,  , ,  nach oben beschränkt folgt im allgemeinen nicht nach oben beschränkt folgt im allgemeinen nicht  . . |

Es sei 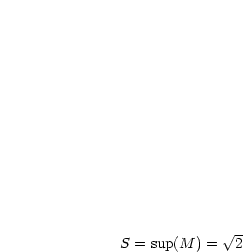 . Dann gilt
. Dann gilt  , das heißt,
, das heißt,  und
und  müssen ausgeschlossen werden. Aus
müssen ausgeschlossen werden. Aus  folgt dann
folgt dann  . Bilde anschließend
mit
. Bilde anschließend
mit  :
:

Für  gelten:
gelten:


Wir nehmen folgendes an:



 ist obere Schranke von
ist obere Schranke von  :
:  . Dies ist ein Widerspruch, da
. Dies ist ein Widerspruch, da  die
kleinste obere Schranke ist.
die
kleinste obere Schranke ist.