3.2 Der Funktionsbegriff

[next] [prev] [prev-tail] [tail] [up]

3.2 Der Funktionsbegriff

Es sei die Zuordnung $f$ : $X '--> Y$ gegeben mit dem Definitionsbereich $D(f )$ und der Bildmenge $R(f) = {y (- Y|$ $E x (- X$ mit $f(x) = y}$ . Eine Funktion ist eine eindeutige Zuordnung:

((f(x1) /= f(x2)) '--> (x1 /= x2) <--> (x1 /= x2) '--> (f(x1) /= f(x2))

Beispiele:

Identität id $x$ :
$f$ : $X '--> X$ , id $x(x) = x$ $A$ $x$
$f : X '--> Y$ , $f (x) = c$ $(c (- M A x)$
Charakteristische Funktion:
${ 1 x (- A f : X '--> {0;1},A < X : xA = 0 x / (- A$
Polynom: $p : R '--> R$

$p(x) = anxn +an- 1xn- 1 + an-2xn-2 + ...+ a1x+ a0$
$a n$ , $a n-1$ , $...$ sind gegebene Zahlen.
Permutation:
$f$ : ${1,2,...,n}$ $'-->$ ${1,2,...,n}$

3.2.1 Gleichheit von Funktionen

Definition:

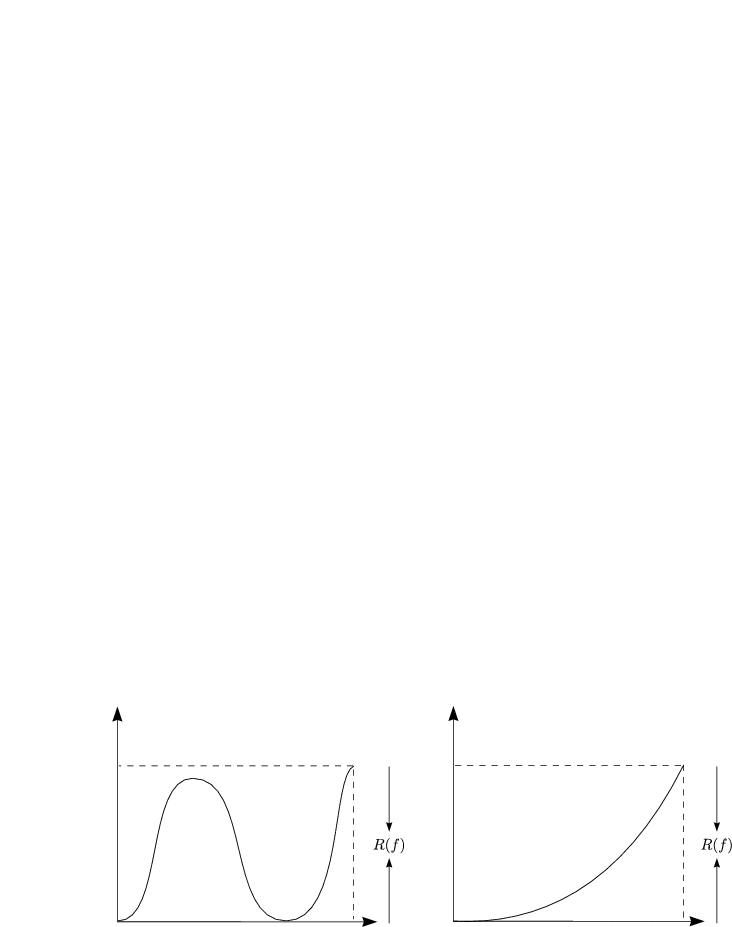
Die Funktionen $f$ : $X '--> Y$ und $g$ : $U '--> V$ seien gegeben. Dann gilt:

$f = g$ $Def ---->$ $X = U$ und $f(x) = g(x)$ $A$ $x (- X$

Beispiel:

$( p) f(x) = sinx g(x) = cos x - 2$
$f(x) = (x +3)3- (x -3)3, g(x) = 12x$

Es gilt $f = g$ für $X = R$ .

3.2.2 Komposition von Funktionen

Beispiel:

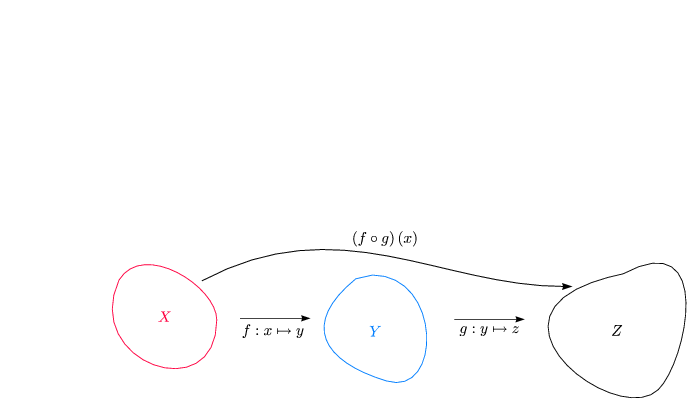
Es seien folgende Funktionen gegeben:

2 f(x) = -x ,X = R

V~ -- + g(x) = x,X = R

Dann bilden wir die Verknüpfung $g o f$ :

V~ --- V~ --2- (go f)(x) = g(f(x)) = f (x) = -x

Diese Verknüpfung ist jedoch im Bereich der reellen Zahlen $R$ nicht definiert.

Beispiel:

$f(x)$ sei folgendermaßen definiert:

V~ ------ f(x) = 1+ x2

h(x) = x2, g(x) = 1 +x, p(x) = V~ x

$f$ folgt dann aus $h$ , $g$ und $p$ durch folgende Verknüpfung:

f = p o go h

Satz:

$X$ , $Y$ , $Z$ , $U$ seien Mengen mit $f : X '--> Y$ , $g : Y '--> Z$ , $g : Z '--> U$ . Dann gilt:

$(ho g)o f$ : $X '--> U$ und $ho (g o f)$ : $X '--> U$ sind definiert, und sie sind gleich.

Gleichung:

$f(x)$	=	$y$
$\|^$		$\|^$
gesucht		gegeben

[next] [prev] [prev-tail] [front] [up]