3.3 Surjektivitt und Injektivitt

3.3 Surjektivität und Injektivität

$f$ heißt surjektiv, falls $R(f ) = Y$ .
$f$ heißt injektiv, falls aus $x1 /= x2$ folgt $f(x1) /= f (x2)$ .
$f$ heißt bijektiv, falls $f$ surjektiv und injektiv ist.

Die Funktion (x1 /= x2) '--> (f(x1) /= f (x2)) <--> f(x1) = f(x2) '--> (x1 = x2)

Beispiel:

2 2 x1 = x 2-- > x1 = ±x2

$X = R$	nicht injektiv
$X = R+$	injektiv
$X = R -$	injektiv

Gegeben: y < Y gesucht: x < X mit f(x) = y

Aus $y (- /R(y)$ folgt: Gleichung ist nicht lösbar!
Ist $f$ surjektiv, so ist die Gleichung stets lösbar.
Ist $f$ injektiv, so ist für $y (- R(f)$ die Gleichung eindeutig lösbar
Ist $f$ bijektiv, so ist die Gleichung stets eindeutig lösbar

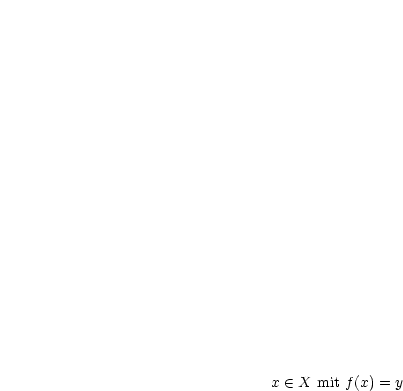$f:X '--> Y$ sei bijektiv, dann gibt es zu jedem $y (- Y$ genau ein $x (- X mit f(x) = y$ . Diese Zuordnung $Y '--> X$ heißt Umkehrfunktion $f-1$ zu $f$ :

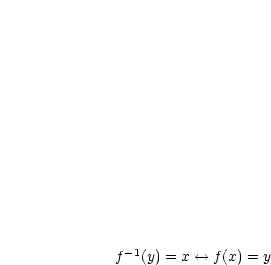f-1(y) = x <--> f(x) = y

(f -1 o f (x)) = f- 1(f(x)) = x A x (f o f-1(y)) = f(f-1(y) = y A y (- Y

f -1 o f = idx f o f-1 = idx

Satz:

Es sei $f : X '--> Y$ bijektiv. Dann ist $f-1$ bijektiv, und es gilt $(f -1)- 1 = f$ .

Satz:

Sind $f : X '--> Y$ und $g : Y '--> Z$ bijektiv, so ist $go f : X '--> Z$ bijektiv und es gilt:

$(go f)-1 = f-1 o g-1$

Zu Satz 2:

Nachzurechnen ist, daß $f-1$ surjektiv und injektiv ist. Für $(f- 1)-1$ argumentiere mit $f-1(y) = x <--> f(x) = y$ .

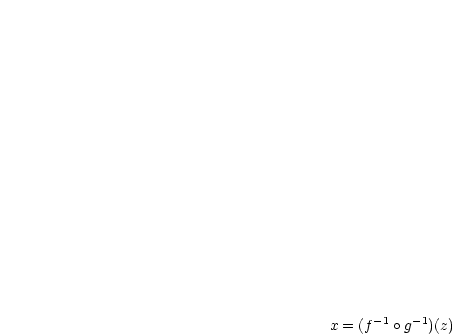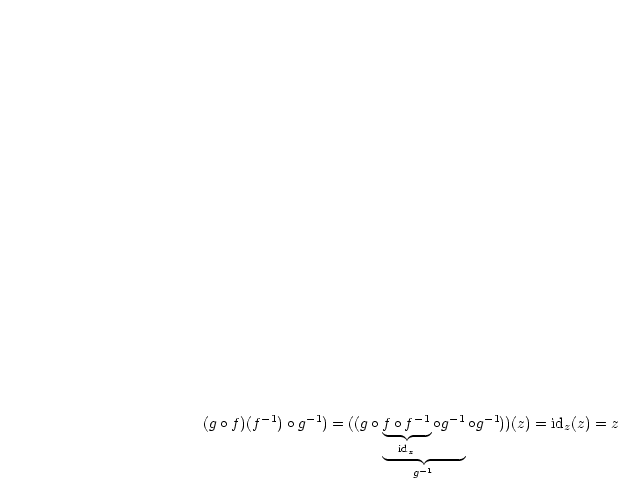
$(go f)(x) = z$ ist lösbar für $z (- Z$ (Surjektivität) $x = (f -1 o g- 1)(z)$ tut es $(g o f)(f-1)o g-1) = ((go f o f-1og-1 og- 1))(z) = id(z) = z -- -- z -idx- ---- g-1$
$go f$ ist injektiv $(go f)(x1) = (g o f)(x2) <--> g(f(x1)) = g(f(x2))-- > f(x1) = f(x2) --surjektiv---$

$(g o f)-1 = f -1 o g- 1$

$(g o f)o (f -1 o g- 1) = id z$

$(f- 1 o g-1)o (go f) = idx$

Beispiele:

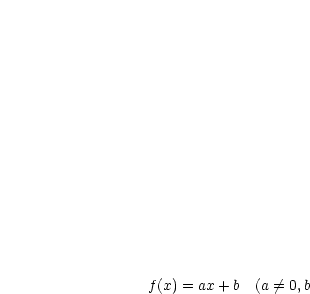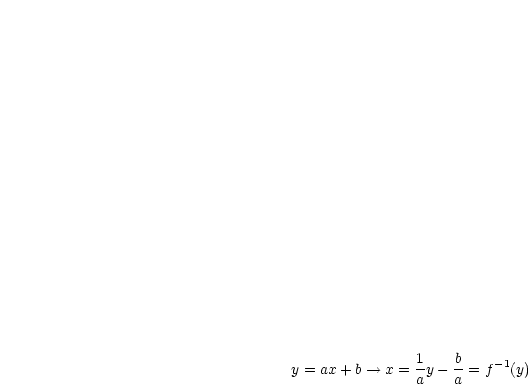
$f(x) = ax + b (a /= 0,b$ gegeben) $X = R$ $y = ax +b --> x = 1y - b-= f-1(y) a a$

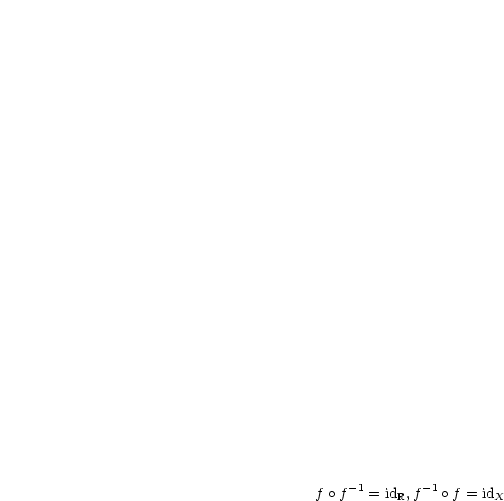
$f o f -1 = idR,f-1 o f = idX$
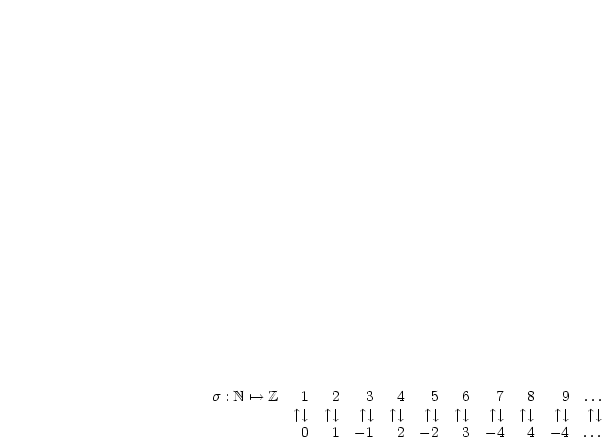
$f : {1$ , $...$ , $n}$ $-->$ ${1$ , $...$ , $n}$ ist surjektiv. Als Übung soll gezeigt werden, daß sie auch injektiv ist.
Daraus folgt dann die Bijektivität einer Permutation.
$s : N '--> Z$
$s$ ist also die Abbildung, welche einer natürlichen Zahl eindeutig eine ganze Zahl zuordnet. Für die Abbildungsvorschrift ergibt sich:
$s(2k) := k fu¨r k = 1,2,...$

$s(2k +1) := - k f¨ur k = 0,1,2,...$
Die Abbildung ist bijektiv, also injektiv und surjektiv. Bijektiv nennt man auch eineindeutig. Im folgenden seien nochmals die Eigenschaften der Verkettung von Abbildung und Umkehrabbildung wiederholt:
$f o f- 1 = idy f- 1 o f = idx$

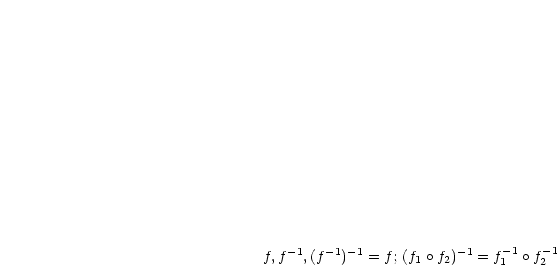
$f,f-1,(f-1)- 1 = f; (f1 o f2)-1 = f-11o f-21$
Wir notieren uns einige Paare:
$s : N '--> Z 1 2 3 4 5 6 7 8 9 ... |^ |, |^ |, |^ |, |^ |, |^ |, |^ |, |^ |, |^ |, |^ |, |^ |, 0 1 - 1 2 -2 3 -4 4 -4 ...$
Verknüpft man also die Abbildung mit deren Umkehrung, so erhält man gerade die Identität:
$s o s- 1 = id$

$- 1 s o s = id$

3.3.1 Monotonie von Funktionen

Definition:

$f : M < R '--> R$ : $f$ heißt streng monoton wachsend ( $f$ $|^$ ) (fallend ( $f$ $|,$ )), falls aus $x1 < x2$ folgt:

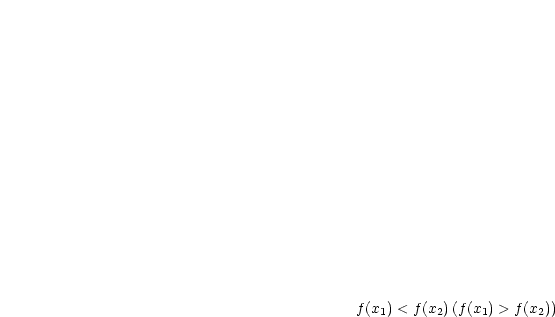
f (x1) < f(x2)(f(x1) > f(x2))

$f$ ist monoton wachsend. $<==>$ $- f$ ist monoton fallend.
Falls $f(x) > 0$ oder $f(x) < 0$ $A x (- M$ gilt: $f$ ist monoton wachsend $<==>$ $1- f$ ist monoton fallend.
$f$ ist monoton wachsend. $<==>$ $(f(x) - f(x ))(x - x ) > 0 1 2 1 2$ $(x /= x ) 1 2$ $<==>$ $f(x )- f(x ) ---1------2-> 0 x1- x2$ für $x1 /= x2$