3.4 Reelle Zahlen

$g$ : ${f : X '--> X bijektiv}$

$f$ , $g (- G$ $==>$ $f o g (- G$
$f$ , $g (- G$ $==>$ $(f o g)o h = f o (g o h)$
Es gibt id $x (- G$ $==>$ $idx o f = f o idx = f$ $A$ $f (- G$
Zu $f (- G$ gibt es $f-1 (- G$ $==>$ $f o f-1 = f-1 o f = idx$

3.4.1 Die Gruppe

Eine nicht leere Menge $G$ zusammen mit einer Abbildung $o$ , durch die je zwei Elemente $a,b (- G$ das Element $ao b (- G$ zugeordnet wird und die folgenden Eigenschaften besitzt, heißt Gruppe:

$ao (bo c) = (ao b)o c$ $A$ $a$ , $b$ , $c (- G$
es gibt ein $n (- G$ mit $n o a = ao n = a$ $A$ $a (- G$
zu jedem $a (- G$ gibt es ein $a' (- G$ mit $a o a'= a'o a = n$

Gilt zusätzlich:

$ao b = bo a A a,b (- G$ , so heißt $G$ abelsche Gruppe

3.4.2 Axiomensystem für die reellen Zahlen

Die reellen Zahlen bilden eine Menge mit den Verknüpfungen + und $.$ :

+ : R× R +(x,y) = x+ y |R × R '--> R (x,y) '--> x+ y (x,y) '--> x + y

Sowie einer Anordnung, die durch eine Teilmenge $R+ < R$ , den Positivitätsbereich, gegeben wird. Für diese Daten müssen erfüllt sein:

Körperaxiome (K):
$(R,+)$ bilden eine abelsche Gruppe mit der 0 als neutrales Element und $- x$ als Inversen zu $x$ . $(R \{0}.)$ ist eine abelsche Gruppe mit der 1 als neutrales Element und mit $1x$ als Inversen zu $x$ .
Es gilt das Distributivgesetz: $x(y+ z) = xy + xz$ $A$ $x$ , $y$ , $z (- R$
Anordnungsaxiome (A)
Vollständigkeitsaxiom (V)

3.4.3 Körperaxiome

Zu gegebenen Zahlen $a,b (- R$ gibt es genau eine Zahl $x (- R mit a+ x = b.(x = b+ (-a))$ . Zu gegeben Zahlen $a /= 0$ gibt es genau ein $x (- R$ mit $ax = b$ $1 (x = ab)$ . Nun gilt:

a.0-=-0 A a- (- -R; (x /= 0,y /= 0 --> xy /= 0)

a + a.0 = a .1+ a.0 = a(1+ 0) = a .1 = a

a+ x = a ==> x = a+ (-a) = 0 = a.0

(-1)(-1) = - (-1) = 1 --------------------

Wir betrachten nun folgende Gleichung:

(-1)+ x = 0 (*)

Diese soll nun gelöst werden:

$(-1)+ (-1)(-1) = (- 1)(1 + (- 1)) = (- 1).0 = 0 (- 1)(- 1)$
$(-1)+ (-(- 1)) = 0 - (-1)$
$(-1)+ 1 = 0$

Die Gleichung wird durch $(- 1)(- 1)$ , $- (-1)$ und 1 gelöst.

3.4.4 Anordnungsaxiome

Die Elemente von $+ R$ heißen positive Zahlen. Diese sind durch die folgenden Axiome gekennzeichnet:

Für jedes $x (- R$ gilt genau eine der Aussagen: $+ + x (- R ,x = 0,-x (- R$
$x,y (- R+$ $==>$ $x + y (- R+$
$x,y (- R+$ $==>$ $xy (- R+$

Bezeichnung: Für $x (- R+$ schreiben wir $x > 0$ .

Definition:

Wir definieren folgendes:

$x < y$ $(y > x)$ $Def ---->$ $y - x > 0$
$y < x$ $Def ---->$ $y < x$ oder $y = x$
$x < y < z$ $Def ---->$ $x < y$ und $y < z$
$x < y < z$ $Def ---->$ $x < y$ und $y < z$
$x$ heißt negativ, falls $x < 0$ gilt. Das heißt: $- x > 0$

Folgerungen:

$x < y < z$ $==>$ $x < z$
$(x < y) /\ (z > 0)$ $==>$ $xz < yz$
$y- x > 0$ , $z > 0$ $==>$ $z(y- x) = zy - zx > 0$ : $zx < zy$
$y < 0$ , $z < 0$ $==>$ $- y > 0$ , $- z > 0$ $==>$ $(-y)(-z)> 0 --- --- yz>0$
$x < 0$ , $z > 0$ $==>$ $xz < 0$ (Setze in 2: $y = 0$ )

Beispiel:

Für welche $x$ gilt $x + 1-> 2 x$ ?

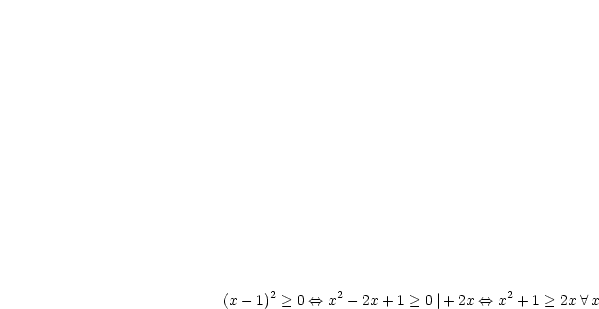
1.Möglichkeit: $2 2 2 (x- 1) > 0 <==> x - 2x + 1 > 0|+ 2x <==> x + 1 > 2x A x$
Für $x > 0$ gilt: $1 x+ --> 2 x$
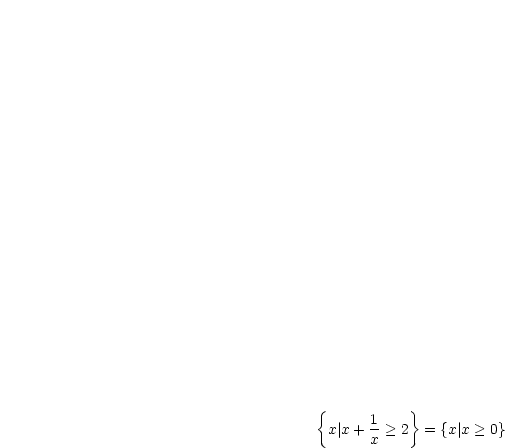
${ 1 } x|x+ x-> 2 = {x|x > 0}$
2.Möglichkeit:
$x + 1-> 2 x$ $==>$ Alle $x$ , die als Lösung möglich sind, sind $> 0$ .
$x2 + 1 > 2x|- 2x <--> x2 - 2x + 1 > 0 <--> (x -1)2 > 0$

$1-> 2 - x x$