6.8 Potenzreihen

$(an)$ sei eine komplexe Zahlenfolge und $z0$ Entwicklungspunkt.

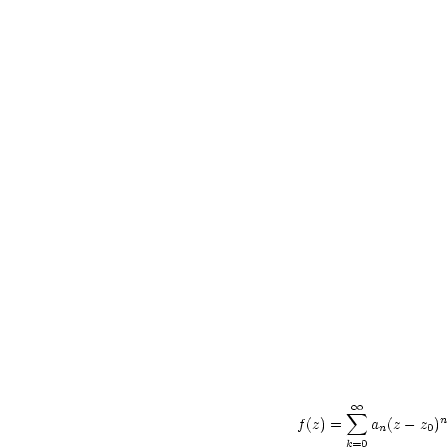
oo f(z) = sum a (z - z)n k=0 n 0

heißt Potenzreihe um $z0$ (mit Entwicklungspunkt $z0$ ). Ohne Beschränkung der Allgemeinheit gilt für $z0 = 0$ :

oo sum k 2 akz = a0 + a1z + a2z + ... (P ) k=0

$(P)$ konvergiert sicher in $z = 0$ . Substituiere $z '--> z':= z - z0$ ( $z'= z$ ).

Lemma:

Konvergiert die Reihe $(P)$ für $z = z1,$ dann konvergiert $(P)$ für alle $z$ : $|z|< |z1|$ absolut und für alle $z$ mit $|z| < r < |z1|$ gleichmäßig und absolut.
Ist $(P)$ in $z = z0$ divergent, so ist $(P)$ divergent für $z :| z|> |z2|$

sum n-1zn (-1) -n ;

z = 1 : 1 - 1 + 1- 1 + ... Konvergenz f¨ur|z|< 1 2 3 4

( ) 1 1 1 z = -1 :- 1+ 2 + 3 + 4 + ... Divergenz f¨ur |z|> 1

Konvergenz f¨ur|z|< 1.

Beweis:

oo sum k k k akz1 sei konvergent. ==> akz1 '--> 0 fu¨r k '--> oo ==> |akz1|< C A k k=0

Es sei $|z|< |z1|$ . Unser Ziel ist zu zeigen, daß $sum oo akzk k=0$ konvergent ist.

| | || zk|| | |||zk|| ||z ||k |akzk| = ||akzk1zk|| = |akzk1|||zk||< C ||z-|| 1 1 1

Dies ist konvergent nach dem Majorantenkriterium, da $| | ||z-||< 1 z1$ . Für $|z|< r < |z1|$ gilt $| | | |k |akzk|< C ||zr1||$ und nach Satz 2 folgt gleichmäßige Konvergenz für $|z|< 1$ . Angenommen, $(P )$ konvergiert gegen $~z$ mit $|~z|> |z| 2$ .

$(P)$ konvergiert für alle $z$ mit $z < |~z|$ , also insbesondere $z2$ Widerspruch
Ist $(P)$ in $z = z0$ divergent, so ist $(P)$ divergent für $z :| z|> |z2|$

Definition:

Gegeben sei: $sum oo k P = akz k=0$ . $r := sup {|z|(P) konvergiert in z}$ . $r$ heißt Konvergenzradius von $(P)$ . ${(z)| z|< r}$ nennt man Konvergenzbereich und ${x,| x|< r}$ ist das Konvergenzintervall.

Beispiel:

Für $sum oo n (- 1)n-1z-- k=1 n$ gilt $r = 1$ .

Satz:

$r$ sei der Konvergenzradius von $P$ .

$r = 0$ : Konvergenz nur in $z = 0$
$r > 0$ : $P$ konvergiert für $z$ : $|z|< r$ absolut und für $|z|< r$ $(0 < r < r)$ absolut und gleichmäßig. Für $|z|> 1$ liegt Divergenz vor.
$r = 0$ : Konvergenz für alle $z (- C$ und gleichmäßige Konvergenz für $|z|< r$ für jedes $r$ .

Folgerung:

$oo sum k akz = p(z) k=0$ sei konvergent für $|z|< r$ . $p(z)$ ist stetig für jedes $z0$ mit $|z0|< r$ . Da $sum n akzk k=0$ stetig und für $|z|< r$ gleichmäßig konvergent ist, ist $sum oo k akz k=0$ stetig für $|z|< r$ , also in $z0$ .

Satz:

Es liegt $sum oo k akz k=0$ vor. Es sei $n V~ ---- a := limsup |an|$ . Dann gilt:

$1 r = a-$ , $r = oo$ , falls $a = 0$ , $r = 0$ , falls $a = oo$
Sind alle $an = 0$ und wenn $|| an || || an || nli'-->m oo ||an+1|| existiert, so gilt: r = nl'-->imo o ||an+1||$ .

------ n V~ k n V~ ---- lim sup |anz |= |z| ,lim sup |an|= |z| a < 1 absolut Konvergenz

V~ ------ V~ ---- lim sup n |anzk|= |z| ,lim sup n |an|= |z| a > 1 Divergenz

Für $|z|< -1 a$ liege Konvergenz vor, für $|z|> 1- a$ liege Divergenz vor. $1 Das heiß t: r =- a$
Voraussetzung: $||an+1 || nli'-->mo o ||-an ||= b$ existiert. $V~ ---- lim n|an|= a n'--> oo$

$| | 1- ||-an-|| ==> a = r = nl'-->imo o |an+1|$

Satz:

Hat $P$ den Konvergenzradius $r > 0$ $(r /= oo )$ , so kann bezüglich Konvergenz oder Divergenz für $|z|= c$ keine allgemeine Aussage gemacht werden. (Dann ist eine zusätzliche Untersuchung notwendig.)

Beispiele:

Anwendung 1: $oo n sum (-1)n-1z-- n=1 n$
Der Konvergenzradius beträgt $r = 1$ . Für $z = - 1$ liegt Divergenz und für $z = 1$ Konvergenz vor.
Anwendung 2: $oo sum zn n=0$
Es gilt $r = 1$ . Divergenz liegt für alle $z$ mit $|z|= 1$ vor.
Anwendung 3: $oo sum zn- n2 n=1$
Es gilt $r = 1$ ; die Reihe ist somit für alle $z$ mit $|z|< 1$ konvergent.
Anwendung 4: $oo sum -22k+2- k V~ k---1z k=2$
Wir schätzen folgendermaßen ab:
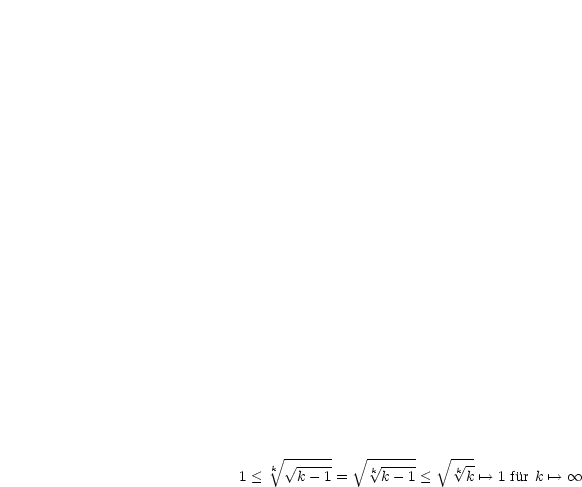
$V~ ------ V~ ------- V~ --- 1 < kV ~ k---1 = k V~ k---1-< k V~ k-'--> 1 fu¨r k '--> oo$
Sodann gilt:
$V~ V ~ --- k k - 1 '--> 1 f¨ur k '--> oo$
Damit folgt nun der Grenzwert:
$[ V~ ------] [ V~ k ] a = lim sup k V~ 22k+2 = lim sup 4.- V~ V ~ -4- = 4 k - 1 k k - 1$
Die Reihe hat den Konvergenzradius $r = 1 4$ .
Anwendung 5: $oo sum 1 k 2kz k=0$

$V~ ---- n V~ ---- k ||1 || [1] 1 a = lim sup |an|= lim sup ||2k ||= lim sup 2 = 2$
Somit folgt:
$1 r = a-= 2$
Anwendung 6: $sum oo (a ) zk mit a (- R und a / (- N /= 0 k=0 k$

$| | | | | | ||-ak-|| ||-a(a--1).....(a---k-+1)-.(k-+-1)!-|| ||k+-1-||k'-->o o r = |ak+1|= |a(a -1) .....(a- k + 1)(a - k).k!|= |a- k |------> 1$

Anwendung:

Wir wollen den Wert folgender Potenzreihe bestimmen:

--------------------- | sum oo (1-) | P = (n+ 1) 4 xn | ----n=0-------n------

Wir spalten die Reihe auf:

( ) ( ) ( ) sum oo 14 n sum oo 14 n sum oo 14 n P = (n + 1) n x = n n x + n x n=0 n=0 n=0

Nun gilt ja bekanntlich:

|------------------| sum oo (r) | | xn = (1+ x)r n=0--n--------------

Also folgt damit für den zweiten Term:

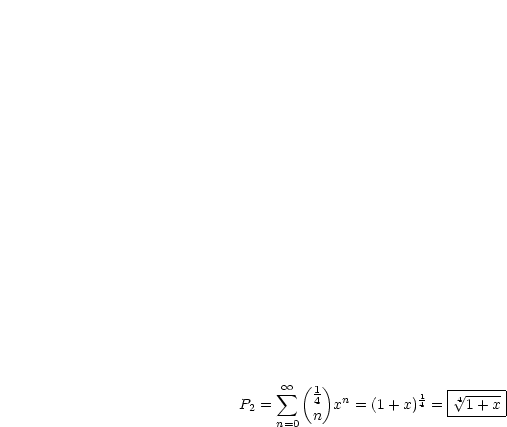
oo (1) |------| P = sum 4 xn = (1 +x)14 =|4 V~ 1-+-x| 2 n=0 n --------

Den ersten Term formen wir zunächst um, woraus dann folgt:

oo (1) oo (1) oo 1 oo 3 P1 = sum n 4 xn = sum n 4 xn = sum ------4!(----)-xn = 1 sum ------(4!---)-xn = n=0 n n=1 n n=1 (n- 1)!n - 14 ! 4n=1 (n - 1)!n - 14 ! sum oo ( 3 ) sum oo ( 3) sum oo ( 3) |----------| = 1 -4 xn = 1 -4 xn+1 = 1 x -4 xn = 1x(x+ 1)-34 = |1 V~ --x----| 4n=1 n- 1 4 n=0 n 4 n=0 n 4 -44-(1+-x)3-

(6.4)

Somit gilt nun für den Wert der Potenzreihe:

1 x V~ ---- 1 1 [ V~ -------] P = P1 + P2 = - V~ 4-----3 + 4x + 1 =- 4 V~ -------3 x+ 4 4(x+ 1)4 = 4 (x+ 1) |------4---(x-+-1)-| 1----x---- |----1----- | = 4 V~ 4(x-+-1)3 [x+ 4x + 4] =|4 4 V~ (x-+-1)3-[5x + 4] -------------------

(6.5)

6.8.1 Identitätssatz für Potenzreihen

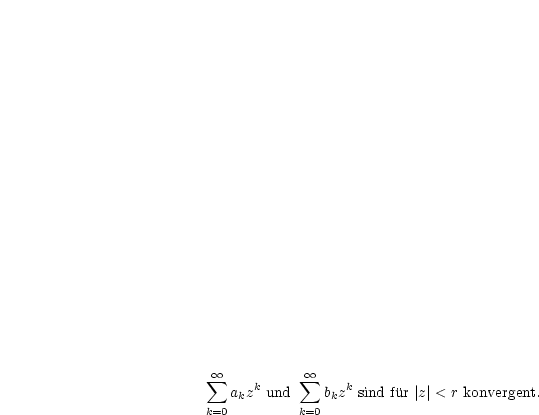
oo sum k sum oo k akz und bkz sind f¨ur |z|< r konvergent. k=0 k=0

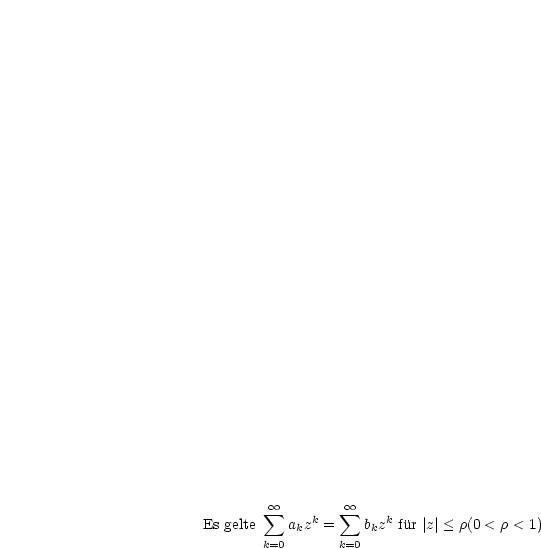
sum oo sum oo Es gelte akzk = bkzk f¨ur |z|< r(0 < r < 1) k=0 k=0

Dann gelten, wie man durch Koeffizientenvergleich findet:

ak = nk,k = 1,2,...

$1 r = ------n V~ ----- lim sup |an |$ heißt Konvergenzradius der Potenzreihe $sum oo anzn n=0$ . Für $|z|< r$ stellt die Reihe eine stetige Funktion $sum oo n f(z) = anz k=0$ , $|z|< r$ dar. Für $|z|> r$ ist die Reihe divergent. Für $|z|= r$ kann sie konvergent sein.

Satz:

Die Reihen $sum oo n anz n=0$ und $sum oo n bnz n=0$ seien für $|z|< R$ konvergent.

Es gelte: $sum oo oo sum anzn = bnzn n=0 n=0$ für $|z|< r(< R)$ . Dann folgt $an = bn$ für $n = 0$ , 1, 2, $...$ .

Wir nehmen an, daß die Behauptung falsch ist. Dann gibt es ein kleinstes $n0 (- N$ mit $an0 /= bn0$ .

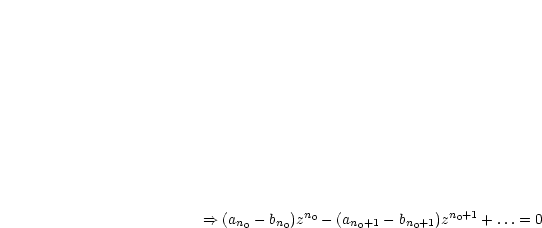
==> (an0- bn0)zn0- (an0+1- bn0+1)zn0+1 + ...= 0

[ ] zn (an0- bn0)+ (an0+1 - bn0+1)z + (an0+2- bn0+2)z2 +... = 0

Wähle $zk = 1 R k$ für $k = 1$ , 2, 3, $...$ und $|zk|< R$ .

zn0 [h(zk)] = 0 ==> h(zk) = 0 k /=0

0 = kli'-->mo o h(zk) = h(kli'-->mo o zk) = h(0) = an0- bn0

Die Reihen sind konvergent, wenn:

( ) ( ) ( ) sum oo oo sum sum oo sum k aj bk = ak-lbl -j=0--- -k=0--- k=0 l=0 absolut konvergent

Dies ist das sogenannte Cauchy-Produkt.

( ) ( ) ( ) oo sum j sum oo k oo sum sum k k ajz bkz = ak-lbl z -j=0 ---- -k=0 ---- k=0 l=0 ra rb --------- --------- r=min(ra,rb)

(z- z )n,f (z ) = a 0 0 0

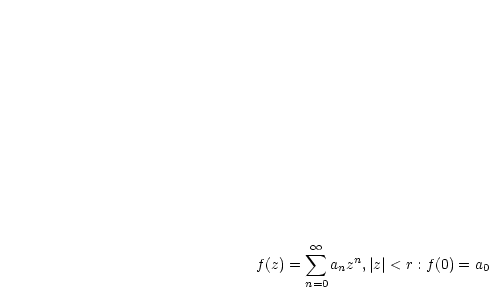
sum oo n f(z) = anz ,|z|< r : f(0) = a0 n=0

Beispiel:

Es sei folgende Potenzreihe gegeben:

oo sum f (z) = anzn f¨ur |z|< r und a0 /= 0 n=0

f(0) /= 0 ==> f(z) /= 0 f¨ur|z|< r(0 < r < r)

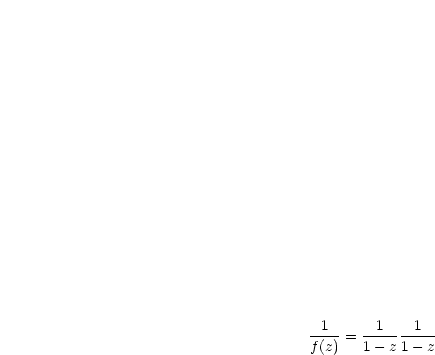
Wir bilden den Kehrwert der Funktion und wollen von dieser neuen Funktion die Potenzreihe wissen:

sum oo -1--= bnzk f¨ur|z|< r f(z) k=0

Gibt es $b0$ , $b1$ , $...$ ? Dazu berechnen wir das CAUCHY-Produkt der beiden Potenzreihen, womit dann folgt:

( ) ( oo sum )( sum oo ) oo sum ( sum k ) oo sum 1 = f(z).--1- = anzk bkzk = ak-lbl zk = ckzk f(z) n=0 k=0 k=0 l=0 k=0 ----c---- k

Damit haben wir nun:

0 1 2 1 = c0z + c1z + c2z + ...

Wir führen einen Koeffizientenvergleich durch. Nur $c0$ hat den Wert 1; alle anderen $ck$ fallen weg:

|------| |1 = c0 | -------

|-----------------------------| | sum k | 0 = ck = ak-lbl f¨ur k = 1,2,... | l=0 | -------------------------------

Der Koeffizient $b0$ folgt nun aus:

|-------| | 1- | 1 = c0 = a0b0 ==> b0 = a0 --------

Damit können wir nun die Koeffizienten $bk$ berechnen:

|------------------------------------------------------| 0 = b0ak + b1ax- 1 + b2ak-2 + ...+ ak-1a1 + bka0 f¨ur k = 1,2,... --------------------------------------------------------

Für $k = 1$ gilt die Gleichung, womit wir $b1$ berechnen können:

0 = b0a1 + b1a0 ==> b1

Für $k = 2$ können wir $b2$ berechnen:

0 = b a + b a + b a ==> b 0 2 1 1 2 2 2

|------------------------------------------------| | -1 | |bk = - a0 [b0ak + b1ak-1 + ...+ak- 1a1] f¨ur k = 1,2,... -------------------------------------------------

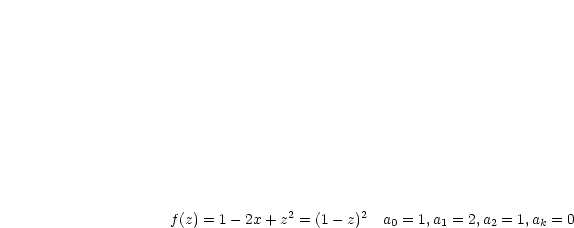
f(z) = 1 - 2x+ z2 = (1 -z)2 a0 = 1,a1 = 2,a2 = 1,ak = 0

-1-- --1----1-- f(z) = 1 - z1 -z

Beispiel:

Betrachten wir die Potenzreihe der Exponentialfunktion:

sum oo 1-k f(z) = k!z ,a0 = 1 /= 0 k=0

Für die Exponentialfunktion gilt:

sum oo --1- = --1---= exp(-z) = bkzk f(z) exp(z) k=0

Wir vermuten nun:

|------------| | k-1 | |bk = (- 1)k!| -------------

1 1- b0 = 1,b1 = -1,b2 = 2,b3 = - 3!,...

Unser Ziel ist es nun, diese Formel für $bk$ zu zeigen: Mit der obigen Beziehung folgt dann:

|------------------| 1 | k- sum 1 1 1 | bk = ---[b0ak + b1ak- 1 + ...+ ak-1a1] =|- (- 1)j---------| a0 ---j=0-----j!(k--j)!-

Des weiteren gelten folgende Beziehungen:

$|-----------------| |(m ) m! | | n = (m---n)!n! | ------------------$ für $n < m$ und $m$ , $n (- N$
$|----------------------| | sum k (k) k- jj k | | j a b = (a + b) | -j=0--------------------|$