
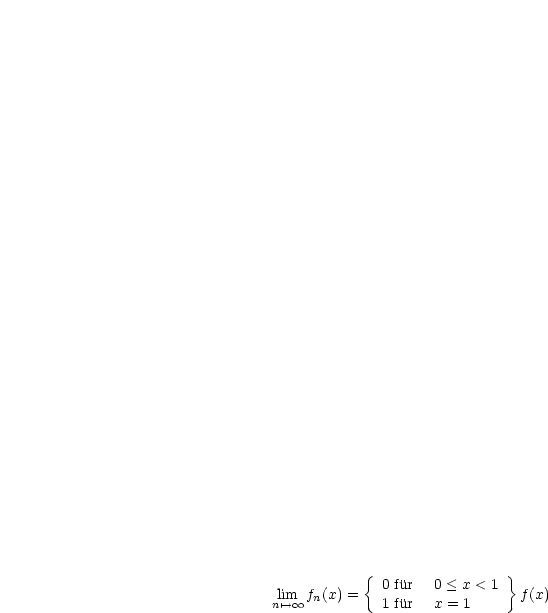
![fn (- C0[0,1]](ma2819x.gif)
![f / (- C0[0,1]](ma2820x.gif)

 für
für  , 3,
, 3,  und
und 
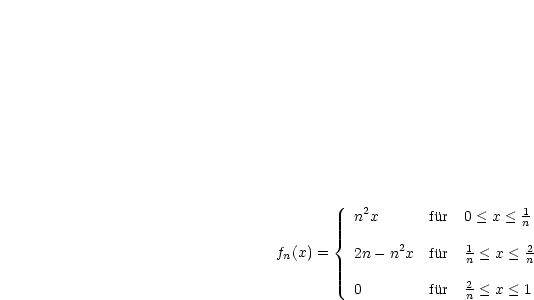
Diese Funktion ist stetig für alle  .
.
![f(x) = nli'-->m oo fn(x) = 0 A x (- [0,1]](ma2828x.gif)


 | (6.3) |
5.  für
für  ,
, 
![x 1[ 1 ] 1
fn(x) =------= --1 - ------ 0 < fn(x) <--
1 +nx n 1+ nx n](ma2835x.gif)

Definition:
|
||||||||||
Gegeben sei die Funktionenfolge Punktweise Konvergenz:
Gleichmäßige Konvergenz:
|
||||||||||
|
||||||||||
Wurzelkriterium:  ist absolut konvergent/divergent, falls
ist absolut konvergent/divergent, falls 

Die Grenzwerte sind gleich.
Definition:
|
Die Grenzfunktion einer auf |
|
Satz:
|
Aus |
|
Beispiel:
Wir betrachten die Exponentialfunktion:

 ist nicht gleichmäßig konvergent für
ist nicht gleichmäßig konvergent für  .
.

Dies ist Gleichmäßig konvergent für  (
( ). Wir wenden den Satz 2
an:
). Wir wenden den Satz 2
an:

Da  , ist
, ist  konvergent.
konvergent.
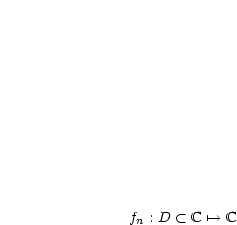

 punktweise.
punktweise. 

 für jedes
für jedes  .
.  punktweise: Zu jedem
punktweise: Zu jedem  gibt es ein
gibt es ein 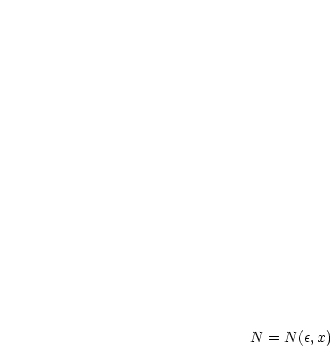 mit
mit 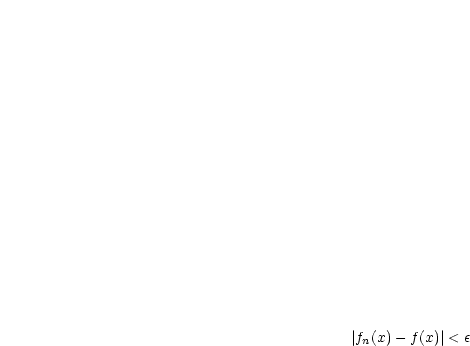
 .
. 
 gleichmäßig auf
gleichmäßig auf 


 gibt es ein
gibt es ein  mit
mit  ,
,
 , falls
, falls 
 .
.  gleichmäßig konvergenten Folge stetiger Funktionen ist stetig.
gleichmäßig konvergenten Folge stetiger Funktionen ist stetig. 

 ,
, 
 und daraus, daß
und daraus, daß  konvergent ist, folgt daß
konvergent ist, folgt daß  auf
auf
 absolut und gleichmäßig konvergiert.
absolut und gleichmäßig konvergiert.