6 Reihen

Kapitel 6
Reihen

6.1 Intervallschachtelung
6.2 Alternierende Reihen
  6.2.1 LEIBNIZ-Kriterium
  6.2.2 Die alternierende harmonische Reihe
6.3 CAUCHY-Kriterium
6.4 Majorantenkriterium
  6.4.1 Quotientenkriterium und Wurzelkriterium
  6.4.2 CAUCHY-Produkt absolut konvergenter Folgen
6.5 Die Exponentialfunktion
  6.5.1 Funktionalgleichung der Exponentialfunktion
  6.5.2 Die reelle Exponentialfunktion
6.6 Stetige Funktionen/Grenzwert von Funktionen
  6.6.1 Zwischenwertsatz
  6.6.2 Stetigkeit der Umkehrfunktion
6.7 Funktionenfolgen/-reihen, gleichmäßige Konvergenz/Potenzreihe-Konvergenzradius
  6.7.1 CAUCHY-Kriterium/Majorantenkriterium
6.8 Potenzreihen
  6.8.1 Identitätssatz für Potenzreihen

Definition:

$(an)$ sei Zahlenfolge: Die Reihe $oo sum ak k=1$ ist die Folge der Partialsummen $n sn = sum ak k=1$ mit $n = 1$ , $2$ , $...$ . Die Reihe $oo sum ak k=1$ konvergiert, falls die Folge $(sn)$ konvergiert. Gilt $sn '--> s$ $(n '--> oo )$ , so schreibt man $oo n sum = s = lim sum a k=1 n'-->o o k=1 k$ . $s$ heißt Wert der Reihe.

Beispiel: Geometrische Reihe:

Es sei $q (- C$ :

sum oo sum n n+1 qk : sn = qk = 1---q--'--> --1--f¨ur n '--> oo und |q|< 1) k=0 k=0 1- q 1- q

Für $|q|< 1$ gilt:

oo sum k --1-- q = 1 - q k=0

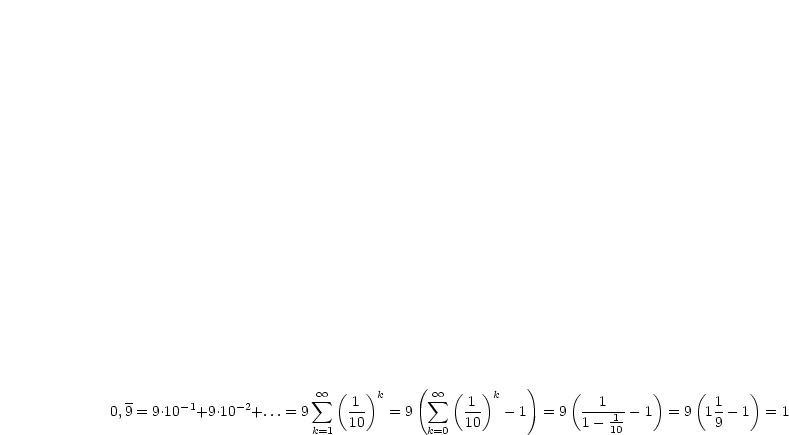
( ) - - 1 - 2 sum oo ( 1 )k sum oo ( 1)k ( 1 ) ( 1 ) 0,9 = 9.10 +9.10 +...= 9 10 = 9 10 - 1 = 9 1---1-- 1 = 9 19 - 1 = 1 k=1 k=0 10

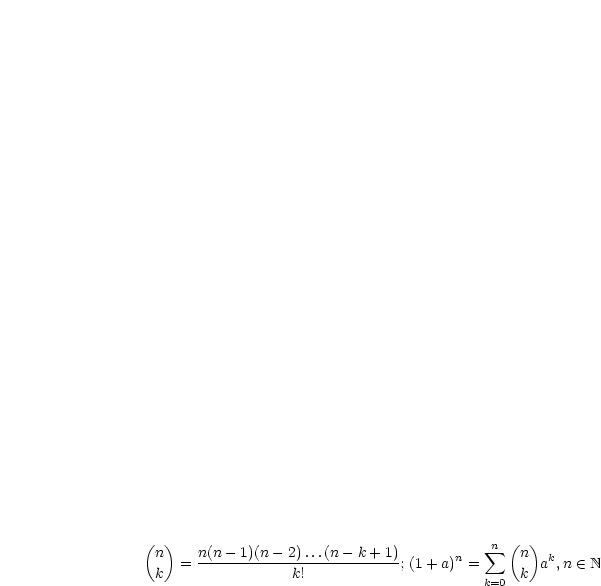
(n ) n(n- 1)(n- 2)...(n - k+ 1) n sum (n) = -------------------------; (1+ a)n = ak,n (- N k k! k=0 k

Die Reihe $oo sum k=0$ ist konvergent mit dem Wert $s$ , falls die Folge $(sn)$ : $n sum sn = ak k=0$ gegen $s$ konvergiert. Konvergiert die Folge $(sn)$ nicht, so heißt die Reihe divergent.

Beispiele:

Harmonische Reihe: $sum oo 1 k-ist divergent. k=1$
Dies wollen wir mittels eines Widerspruchbeweises zeigen. Angenommen, die Reihe ist konvergent und habe den Grenzwert $s$ :
$sum n 1- sn = k '--> s k=1$
Außerdem gilt
$1 1 1 1 1 1 1 s2n = 1+ 2 + 3 + 4+ 5 + 6 +...+ 2n---1 + 2n-'--> s(n '--> oo ) - 1 - 1 ----1---- > 2 > 3 >n$
Somit folgt nun:
$s > s + 1------> s > s + 1 ==> 0 > 1 2n n 2 n'--> oo 2 2$
Dies ist ein Widerspruch, die Reihe ist also divergent.
Geometrische Reihe:
$sum oo k q k=0$ ist konvergent mit dem Wert $-1--- 1- q$ , falls $|q|< 1$ ist.
$oo sum ---1--- oo sum -1 k(k- 1) = 1, k2 ist konvergent. k=2 k=1$

$oo -1---= sum qk = q0 +q1 + q2 +...|q| < 1 1- q k=0 =1$

Übung (ehemalige Klausuraufgabe):

( ) sum oo 1+-i n 2 k=0

$00$ ist unbestimmt.

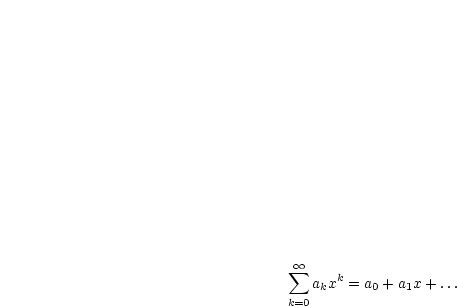
sum oo k akx = a0 + a1x+ ... k=0

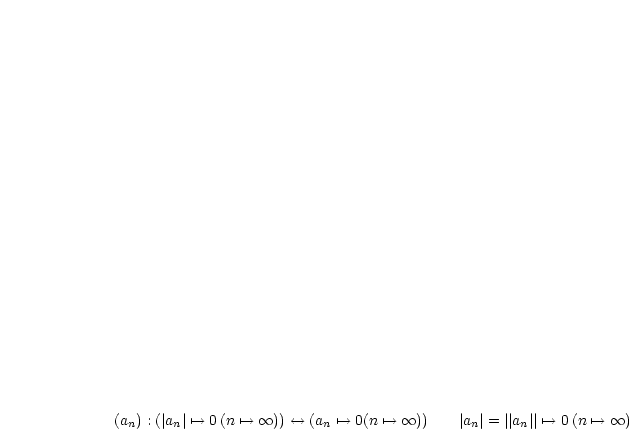
(an) : (|an|'--> 0(n '--> oo )) <--> (an '--> 0(n '--> oo )) |an|= ||an||'--> 0(n '--> oo )

Beispiel:

sum oo -1 = 1+ 1 + -1--+ --1---+ ... k=0k! 2.1 3.2.1

Es gilt $sn < sn+1$ , damit ist $(sn)$ monoton steigend.

n sum -1( )k sum oo ( )k sn = 1+ 1-+ 1-+--1-- + ---1----+ ...+ --------1---------< 1+ 1 < 1+ 1 = 3 20 21 3-.2.1 4.3.2-.1 1.2-.3-.....(n---1)n k=0 2 k=0 2 122- 123 21n--1

Das heißt, $sum oo 1 -- k=0k!$ ist konvergent mit dem Grenzwert e, wobei feststeht, daß $52 < e < 3$ sein muß.

Beispiel:

Es sei $c > 0$ fest.

V~ - lim n c = 1 n'-->o o

Es gilt bekanntlich:

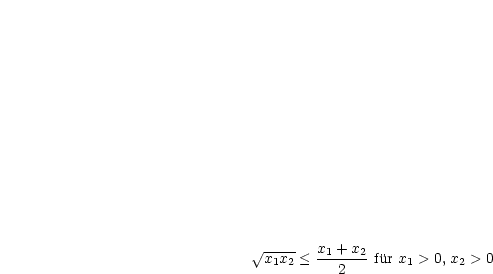
V~ x-x-< x1 +-x2-f¨ur x > 0, x > 0 1 2 2 1 2

Dies ist ein Spezialfall der Ungleichung zwischen geometrischem und arithmetischen Mittel, welche als Übung gezeigt werden kann:

| V~ ---------------x-+-x-+-...+-x-----------| | x1 .x2 .....xn <-1--2--------n-f¨ur xj > 0| -------------------------n-----------------|

1.Fall: $c > 1$ $V~ ----------- c+ (n- 1) c 1 nc .1.1-.....1 < ----n-----= n-+ 1- n- n-1$

$lim n V~ c-= 1,c > 1 n'--> oo$
2.Fall: $c < 1$ $V~ -- n 1 = -1 V~ - '--> 1 f¨ur n '--> oo : n V~ c-=-1- '--> 1 f¨ur n '--> oo c nc -1n V~ c$
Für $an > 0$ gelte $an+1-< K an$ für fast alle $n > N$ .

Aufgabe:

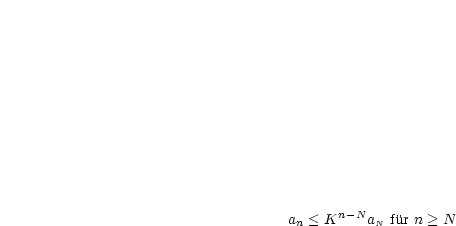
an < Kn-N aN f¨ur n > N

Man kann dies durch vollständige Induktion beweisen:

Induktionsanfang: $n = N$ für $aN < aN$
Induktionsschluß:
- Induktionsvoraussetzung: $n-N an < K aN f¨ur n > N$
- Induktionsbehauptung: $an+1 < Kn+1 -NaN$
  
  $n-N an+1 < Kan < KK aN$
  
  $V~ --- n V~ ------- nan < K K-N aN$

Satz:

Es sei $an > 0$ für $n (- N$ . Dann gilt:

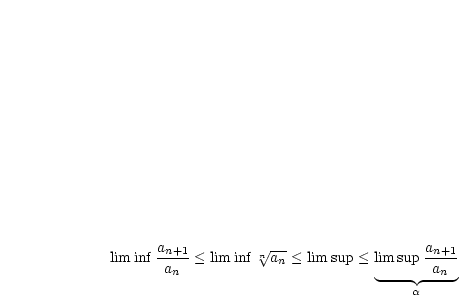$lim inf an+1 < lim inf n V~ an-< lim sup < lim sup an+1 an ---- --an a$

Für $a < oo$ gilt $an+1 < a+ e an - - K$ für $n > N$ und $V~ ----------- V~ nan-< (a + e) n (a + e)- Nan$ .

$lim sup n V~ an-< a+ e A e > 0 --> lim sup V~ 3an-< a$

Satz (Folgerung aus vorhergehendem Satz):

Sei $(an)$ eine Folge positiver Zahlen und existiert $lim an+1 n'-->o o an$ , dann existiert $lim n V~ an- n'-->o o$ und beide Grenzwerte sind gleich.