6.6 Stetige Funktionen/Grenzwert von Funktionen

Es sei $f$ : $D < C '--> C$ . $z0$ sei ein Häufungspunkt des Definitionsbereiches $D$ . $z0$ sei Grenzwert von $(zn),zn (- D$ . Unser Ziel ist es zu klären, was $limz'-->z0 f (z)$ mathematisch bedeutet (Grenzwert von $f$ bei Annäherung $z '--> z0$ ).

$limn'--> oo an = a$ : Zu jedem $e > 0$ gibt es ein $N (e) (- N$ , so daß aus $n > N(e)$ folgt: $|an -a|< e$ .
$limz'-->z0 f(z) = A$ : Zu jedem $e > 0$ gibt es eine Umgebung $Ud(e)$ von $z0$ , so daß aus $z (- Ud(e)$ ( $|z- z0|< d(e))$ folgt: $|f(z)- A |< e$ .

Definition:

$lim f(z) = A z'-->z0$ bedeutet: Zu $e > 0$ gibt es ein $d(e,z0) > 0$ derart, daß aus $0 < |z- z0|< d z (- D$ folgt

$|f(z)- A|< e$ .

Satz:

$zli'-->mz0f(z) = A$ $<-->$ für jede Folge $(zn) < D$ , $zn '--> z0$ gilt: $f(zn) '--> A$ $(n '--> oo )$ .

Anwendung:

$zli'-->mz0f(z)$ existiert nicht, falls es eine Folge $(zn) < D$ mit $zn '--> z0$ so gibt, daß $f(zn)$ nicht konvergiert. $lim f(z) z'-->z0$ existiert nicht, falls es zwei Folgen $(zn)$ , $(z'n) < D$ gibt, für die $zn '--> z0$ und $' zn '--> z0$ konvergieren mit $f(zn) '--> A1$ $(n '--> oo )$ und $' f(zn) '-->$ $' A$ .

f ist in z0 (- D stetig <--> lim f(z) = f(z0) z'-->z0

Zu jedem $e > 0$ gibt es ein $d(z0,e) > 0$ derart, daß aus $z (- D$ und $|z- z0|< d$ folgt:

|f(z)-f (z0)|< e <--> F¨ur jede Folge (zn) < D mit lim zn = z0 gilt: lim f(zn) = f(z0). n'--> oo n'-->o o

Es sei $0 C (D) = {f|f$ stetig für jedes $z (- D}$ :

$id$ : $C '--> C$ : $id(z) = z$ stetig für jedes $z 0$ : $|id(z)- id(z0)|= |z- z0|< e d = e$
$f(z) = exp(z)$ ist stetig für jedes $z0 (- C$ . $lim exp(z) = lim exp((z - z0) + z0) = lim exp(z - z0)exp(z0) = 1exp(z0) z'-->z0 z'-->z0 z'-->z0$
$f(z) = |z|$ ist stetig für jedes $z0 (- C$ : $||z|- |z0||< |z- z0|(Dreiecksungleichung)$

$Wa¨hle d = e$
$f : R+ '--> R$ : $V~ -- f(x) = x$ ist stetig für alle $x0 > 0$ .
Stetig bei $x0$ : $e > 0$ sei gewählt. $d = e V~ x0$
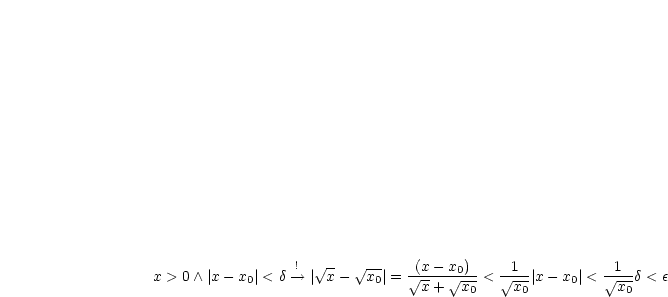
$x > 0 /\ |x - x0|< d--->! | V~ x-- V~ x0-|= V~ (x--x V~ 0)-< V~ 1-|x- x0|< V~ 1-d < e x+ x0 x0 x0$

Satz:

$f$ , $g$ : $D < C$ , $z0 (- D$ . $f$ , $g$ seien in $z0$ stetig. Dann sind $f + g$ , $cf(c (- C)$ , $f o g$ , $f- g$ : ${z (- D |g(z) /= 0}$ $(g(z0) /= 0)$ in $z0$ stetig.

Sei $(zn)$ eine Folge mit $zn '--> z0$ $(n '--> oo )$ . Ziel: $(f + g)(zn) '--> (f + g)(z0)$ $(n '--> oo )$ .

$f(z1)+ g(z1) '--> f(z0 + g(z0)$
$f(zn) '--> f (z0),g(zn) '--> g(z0)(n '--> oo )$ (Sätze über Folgen)

Bemerkung:

g sei in z stetig und g(z ) /= 0. Dann gilt: g(z) /= 0 f¨ur|z-z |< j.(in Umgebung von z) 0 0 0 0

1 1 Wa¨hle e = 2|g(z0)|> 0.Es gibt d > 0 mit |z- z0|< d --> |g(z)- g(z0)|< 2|g(z0)|

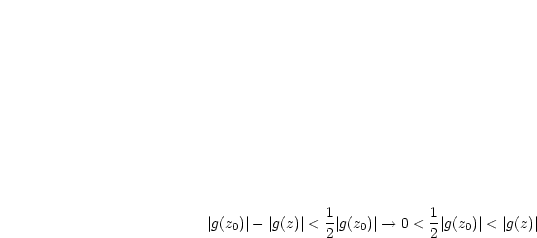
|g(z )|- |g(z)| < 1| g(z )|--> 0 < 1|g(z )|< |g(z)| 0 2 0 2 0

Ziel:

(go f)(xn) '--> (go f)(x0)(n '--> oo ).

g(f(xn)) '--> g(f(xn))(n '--> oo ).

Dies gilt für $yn = f(xn)$ .

Beispiele:

$|.|$ ist stetig und $f$ ist stetig. Dann ist auch $|f|$ stetig.
Aus der Stetigkeit von $exp(z)$ folgt die Stetigkeit von $|exp(z)|$ .
$f$ sei stetig auf $R$ für $f(x) > 0$ .
Aus der Stetigkeit von $exp(x)$ und $V~ - f$ ergibt sich die Stetigkeit von $V~ ------ exp(x)$ .
Da $(x) = x$ stetig ist, folgt auch die Stetigkeit von $2 g(x) = x$ und damit auch die Stetigkeit von $2 h(x) = exp(x )$ .
$f$ , $g$ seien stetig auf $I$ . Dann gilt: $M (x) = max(f(x),g(x)) ist stetig auf I.$

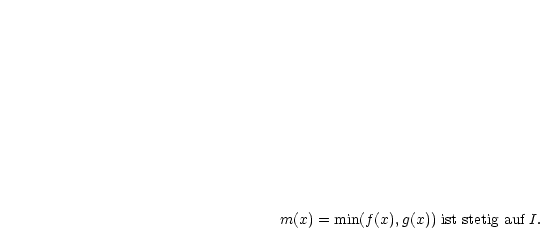
$m(x) = min(f(x),g(x)) ist stetig auf I.$

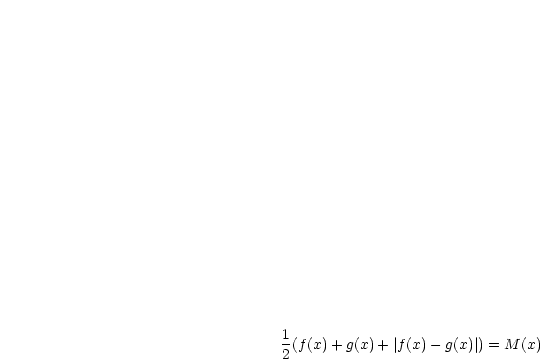
$1 (f(x)+ g(x)+ |f(x)- g(x)|) = M (x) 2$

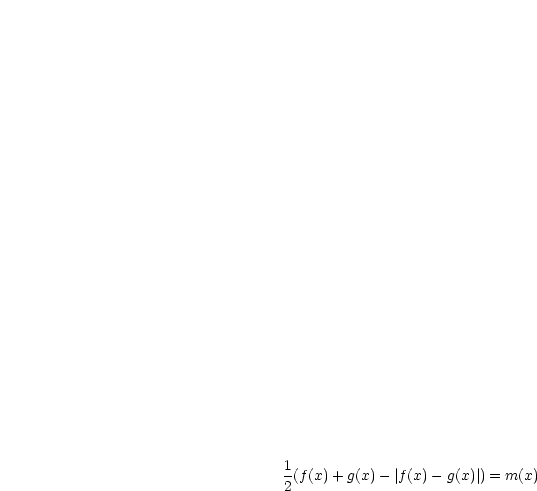
$1(f (x) +g(x)- |f(x)- g(x)| ) = m(x) 2$

Satz:

$[a,b]$ sei abgeschlossenes, beschränktes Intervall: $f (- C0[a,b]$ mit $f(a) < 0,f(b) > 0$ . Dann gibt es ein $x (- (a,b) 0$ mit $f(x ) = 0 0$ .

Beweis:

Konstruiere eine Intervallschachtelung $[an,bn]$ : $an < bn$ , $an < an+1$ , $bn+1 < bn$ , $bn- an '--> 0$ . Induktiv setzen wir $a0 = a$ , $b0 = b$ (Anfang). Für $n > 0$ seien $[a0,b0]$ , $[a1,b1]$ , $...$ , $[an,bn]$ schon konstruiert. Das Problem ist die Definition von $[an+1,bn+1]$ . Bilde $m = 1(an + bn) 2$ und berechne $f(m)$ :

$f(m) = 0$ mit $m = x0$
$f(m) < 0$ , wähle: $an+1 = m,bn+1 = bn$
$f(m) > 0$ , wähle: $an+1 = an,bn+1 = m$

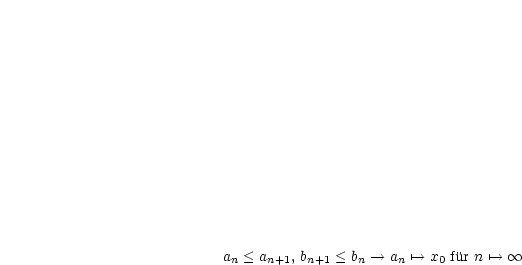
an < an+1, bn+1 < bn-- > an '--> x0 f¨ur n '--> oo

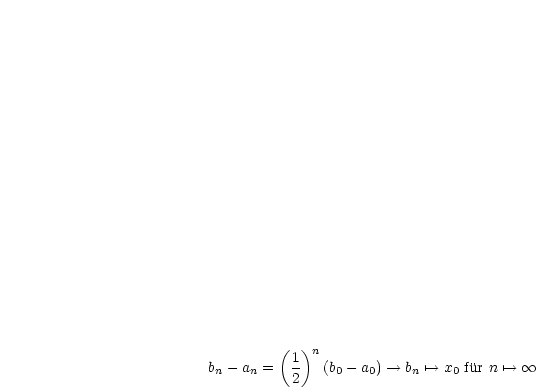
( )n bn- an = 1 (b0- a0)-- > bn '--> x0 f¨ur n '--> oo 2

==> an < bn, an < x0 < bn

f(a ) < f(b ) n n

lim f(x0) < 0 < f(x0)-- > f(x0) = 0 n'-->o o

Folgerung 1 (Zwischenwertsatz):

$0 f (- C [a,b]$ $(f(a)- c)(f(b)- c)) < 0$ . ( $c$ liegt zwischen $f (a)$ und $f(b)$ . Dann existiert ein $x0 (- (a,b)$ mit $f(x0) = c$ .

Beweis:

Wende für $g(x) = f(x) - c$ den vorherigen Satz an.

Beispiele:

Es sei $n (- N$ und $a > 0$ . $xn = a$ hat genau eine positive Lösung $x0 = V~ na$ .

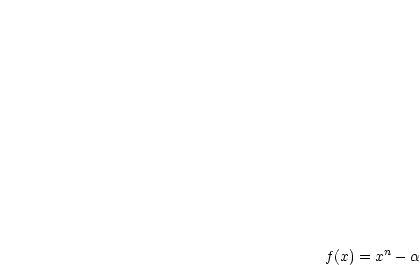
f(x) = xn- a

f(0) = - a < 0, f (1 + a) = (1+ a)n; a > 1 > 0 > 1+ na - a

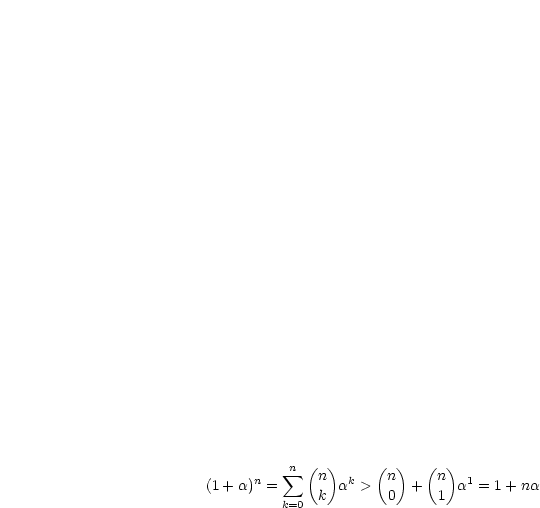
n sum n (n ) k (n ) (n ) 1 (1 + a) = k a > 0 + 1 a = 1+ na k=0

Daraus folgt, daß in $(0,1+ a)$ die Funktion $f$ eine Nullstelle $x0 > 0$ mit $n x0 = a$ besitzt.

{ xn= a } n-1 n-2 n-3 n-1 x0n= a xn0 - xn1 = (x0--+-x0--x1 +-x0-x21 +-...+-x1-)(x0 - x1) = 0 1 >0

Folgerung 2:

$0 f (- C [a,b]$ sei streng monoton. Dann bildet $f$ das Intervall $[a,b]$ injektiv und surjektiv auf $[f(a),f(b)]$ $( |^ )$ bzw. $[f(b),f(a)]$ $( |, )$ ab.

6.6.1 Zwischenwertsatz

Definition:

$[a,b]$ ist beschränktes abgeschlossenes Intervall, $f (- C0[a,b]$ . $C$ liege zwischen $f(a)$ und $f(b)$ . Dann gibt es ein $x0 (- [a,b]$ mit $f(x0) = c$ .

Folgerung:

Ist $f (- C0[a,b]$ streng monoton wachsend, so ist $f[a,b] '--> [f (a),f(b)]$ bijektiv. Stetigkeit in $x0$ bedeutet:

limn'--> oo f (xn) = f(nli'-->m oo xn)(xn '--> x0 f¨ur n '--> oo )

Satz:

$f$ , $g$ seien stetig in $z0$ . Dann folgt daraus:

$f + g$ ist stetig in $z0$ .
$cf$ ist stetig in $z 0$ .
$C0(D)$ bilden mit „+ und skalarer Multiplikation einen Vektorraum.

{ f (x) = x f¨ur 0 < x < 1 x -1 f¨ur 2 < x < 3

{ x f¨ur 0 < x < 1 f (x) = x +1 f¨ur 1 < x < 2

Die Funktion ist in $x = 1$ unstetig!

6.6.2 Stetigkeit der Umkehrfunktion

Satz:

Es sei $f : [a,b] '--> R$ stetig und streng monoton wachsend. Die dann definierte Umkehrfunktion $f-1 : [f (a),f(b)] '--> [a,b]$ ( $f- 1(y) = x$ $<-->$ $f(x) = y$ ) ist stetig und streng monoton wachsend.

Satz:

$f (- [a,b]$ . Dann gelten:

Es gibt eine Zahl $k > 0$ mit $|f(x)|< k$ $A$ $x (- [a,b]$ .
$f$ nimmt den größten und kleinsten Wert an. Das heißt: Es gibt $x0$ , $y1 (- [a,b]$ mit $f(x1) < f(x) < f(x0)$ $A$ $x (- [a,b]$ .

Beweis:

. Angenommen, der Satz ist falsch: Zu jeder Zahl gibt es ein : $f(xn) > n.$
$(xn)$ ist beschränkte Folge, die somit einen Häufungspunkt $x0 (- [a,b]$ besitzt. Es gibt eine Teilfolge $(xnk)k$ mit $xnk '--> x0(k '--> oo )$ .
- $f(xnk) > nk$
- $f(xnk) '--> f(x0)$ für $k '--> oo$
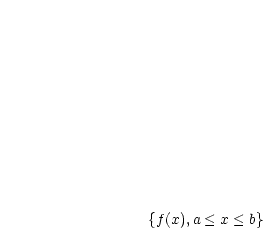${f(x),a < x < b}$ ist beschränkt, $/= P$
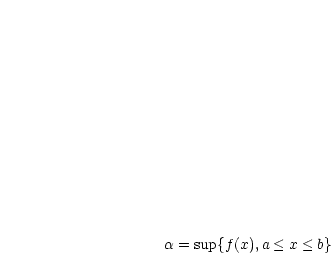Es gibt ein $a = sup{f(x),a < x < b}$ . Ziel: Es gibt ein $x0 (- [a,b]$ mit $f(x0) = a$ . Für jedes $e > 0$ gibt es damit ein $x (- [a,b]$ mit $a - e < f(x)$ , $a - f(x) < e$ $(*)$ . Angenommen, es ist $f(x) /= a$ $A$ $x (- [a,b]$ , dann folgt, daß $--1--- g(x) = a-f(x)$ in $f[a,b]$ stetig ist. $g$ ist beschränkte Funktion: Aus $(*)$ ergibt sich, daß es zu jedem $e > 0$ ein $x (- [a,b]$ gibt mit $1 g(x) < e$ . Dabei handelt es sich um einen Widerspruch. Damit ist der Satz bewiesen.

[next] [prev] [prev-tail] [front] [up]