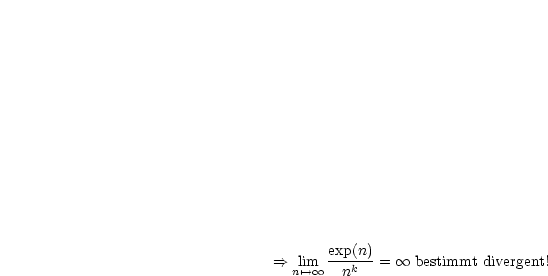gegeben. Dann betrachten wir folgende Reihe:
gegeben. Dann betrachten wir folgende Reihe:
Es sei  gegeben. Dann betrachten wir folgende Reihe:
gegeben. Dann betrachten wir folgende Reihe:
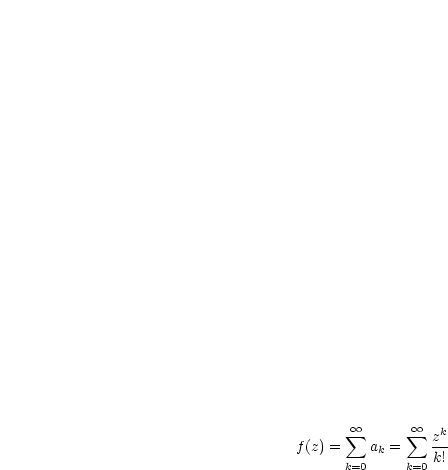
Wir untersuchen die Reihe auf Konvergenz:

Aus dem Quotientenkriterium folgt, daß  für jedes
für jedes  absolut
konvergiert.
absolut
konvergiert.
|
Für jedes |
|
|
|
|
|
Für  gilt gilt 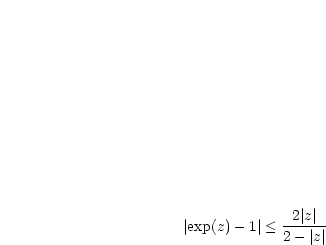 |
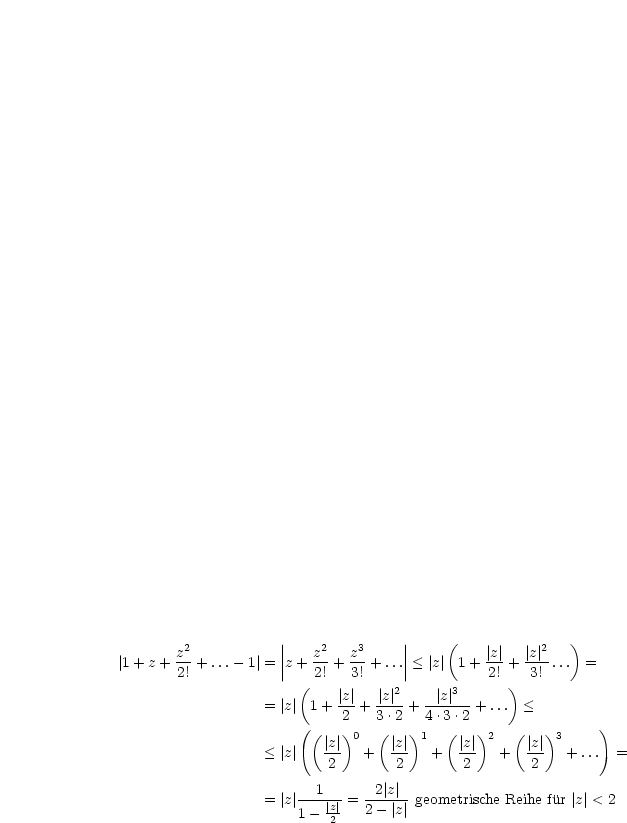 | (6.1) |
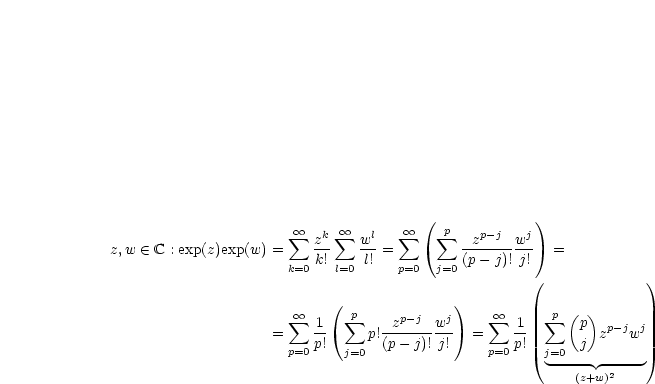 | (6.2) |

 |
 |
|

 , Ziel:
, Ziel: 


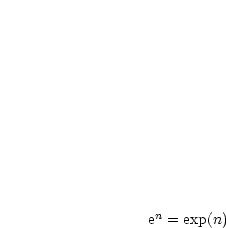 ,
,  Wir beweisen dies mit vollständiger Induktion:
Wir beweisen dies mit vollständiger Induktion:
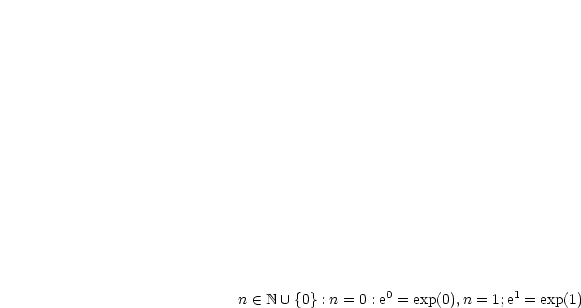
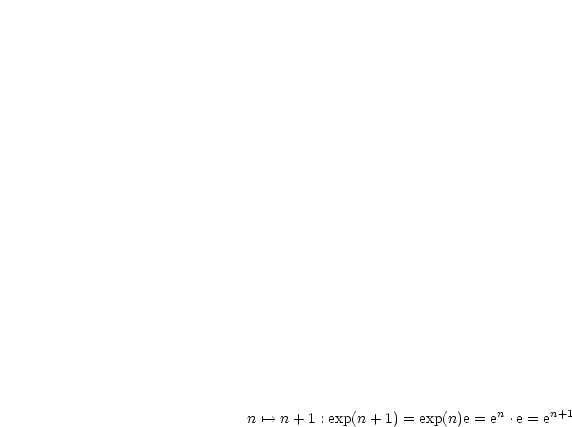

 ?
?