6.4 Majorantenkriterium

Satz:

$sum oo ck k=0$ sei konvergent. $a0$ , $a1$ , $a2$ , $...$ sei Zahlenfolge mit $|an|< cn$ für alle $n$ . Dann konvergiert $sum oo ak k=0$ absolut.

$( ) oo sum sum oo ck heißt konvergente Majorante f¨ur ak. k=0 k=$

$sum n sn = ck k=0$ , $(sn)$ $|^$ , $sn '--> s$ $(n '--> oo )$ , $sn < s$ $A$ $n$

$sum n sn = |ak| k=0$ : $(sn)$ $|^$ : $sn < sn < s$ ist nach oben beschränkt. Daraus folgt, daß $sn$ konvergent ist.

Beispiel:

oo k2 < k3 : 1-<-1 ==> sum 1- ist konvergent. k2 k3 k=1 k2

Satz (Majorantenkriterium):

$(cn)$ , $(an)$ seien reelle Zahlenfolgen mit $0 < cn < an$ $A$ $n$ . Die Reihe $oo sum cn n=0$ sei divergent. Dann ist $oo sum an n=0$ divergent. $sum cn$ ist divergente Minorante für $sum an$ .

Beweis:

Negation von Satz 6

Beispiel:

oo V~ - V~ 1 -1 sum V~ 1- k < k : k > k > 0 : k ist divergent. k=1

Beispiel:

n n Vorbemerkung: sum V~ -----1- V~ -----> 2 sum -1---= 2n-+-1'--> 2 f¨ur n '--> oo k=0 n- k +1 k+ 1 n=0 n+ 2 n + 2

Nach $V~ ab < 1(a+ b) 2$ folgt:

V~ ---------------- 1 (n- k + 1)(k + 1) < 2(n+ 2)

Die Reihe $oo sum (- 1)k V~ -1--= s k=0 k +1$ ist konvergent nach LEIBNIZkriterium, aber nicht absolut konvergent (siehe oben)! Folgende Reihe ist divergent:

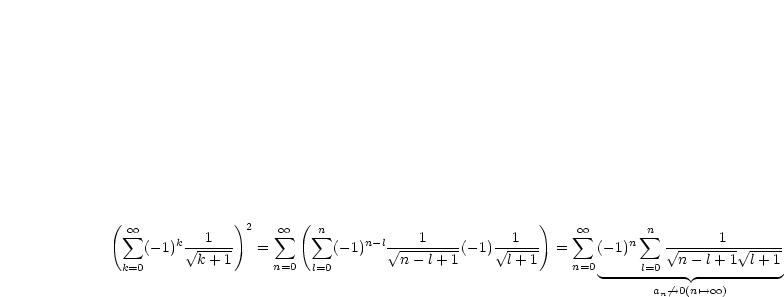
( ) ( ) sum oo k 1 2 sum oo sum n n- l 1 1 oo sum n sum n 1 (-1) V~ k-+-1 = (- 1) V~ n---l+1-(- 1) V~ l+-1 = (- 1) V~ n---l+-1 V~ l-+-1 k=0 n=0 l=0 n=0 ----l=0--- ---------- an/-->0(n'-->o o )

6.4.1 Quotientenkriterium und Wurzelkriterium

Satz (Kapitel 9 im Skript):

Wir betrachten die Reihe $oo sum ak k=0$ mit $ak /= 0$ . Dann gilt:

$( ) ( ) n V~ ---- an+1 an+1 r := lim sup |an|,r = lim inf an ,R = lim sup an$

$sum oo 1 k- k=1$ : $r = r = R = 1$ $oo sum 1 k2 k=1$ : $r = r = R = 1$

Beispiele:

sum oo ak = 1+ 1+ -12 + 12 + ... r = V~ 1-,r = 0,R = oo k=1 2 3 2 3 2

sum oo ak = 1+ 1 + 1+ 1+ -1 + 1-+ -1-+ ... r = r = R = 1 k=1 2 8 4 32 16 128

r < r < R

Satz (Wurzelkriterium):

$oo sum a k=0 k$ liegt vor. $r = lim sup n V~ |a-| n$ Es gelten:

$r < 1$ : absolute Konvergenz der Reihe $sum ak$ .
$r > 1$ : Divergenz
$r = 1$ : keine allgemein verbindliche Aussage hinsichtlich Konvergenz/Divergenz möglich

Beweis des Wurzelkriteriums:

Wähle $q$ mit $r < q < 1$ . Aus der Definition von $r$ folgt $n V~ ---- |an|< q$ $A$ $n > N$ . Damit ergibt sich $n |an|< q$ für $n > N$ . Mit dem Majorantenkriterium folgt die Behauptung, da $oo sum qn n=0$ wegen $0 < q < 1$ konvergiert. Für $r > 1$ (das heißt nach $n V~ |an|> 1$ für unendlich viele $n$ ) gilt $|an|> 1$ für unendlich viele $n$ . Daraus ergibt sich, daß $an '--> 0$ für $n '--> oo$ nicht möglich ist und hieraus wiederum folgt die Divergenz.

Satz:

Quotientenkriterium: $sum oo ak k=0$ soll untersucht werden. $(an+1) (an+1) r = lim inf an-- ,R = limsup -an-$ .

Dann gelten:

$R < 1$ : Absolute Konvergenz liegt vor.
$r > 1$ : Divergenz liegt vor.
$r < 1 < R$ : Keine verbindliche Aussage ist möglich.

Beweis:

r < r < R : R < 1 --> r < 1 --> absolute Konvergenz

r > 1 --> r > 1-- > Divergenz

1.) und 2.) sind Reihen, die wegen $r < 1$ nach dem Wurzelkriterium absolut konvergent sind. Für 1.) und 2.) liefert das Quotientenkriterium wegen $r < 1 < R$ keine Aussage.

Bemerkungen:

Existieren $---- gW = lim n V~ |an |(= g) n'-->o o$ oder $| | gQ = lim ||an+1||(= r = R) n'-->o o | an |$ , so hat man:

gW < 1 absolute Konvergenz gQ < 1 gW > 1 Divergenz gQ > 1 gW = 1 keine Aussage gQ = 1

Betrachten wir die Sonderfälle 1.) und 2.) Für $r < r < 1 < R$ ist das Wurzelkriterium besser als Quotientenkriterium. Für $r < 1$ , $r < R$ ist sowohl das Quotientenkriterium als auch das Wurzelkriterium anwendbar. Für die absolute Konvergenz von $sum a k$ ist zu zeigen: