6.3 Cauchy-Kriterium

6.3 CAUCHY-Kriterium

Satz (Skript Seite 820):

$(a ) n$ sei Zahlenfolge. $(a ) n$ ist konvergent $<==>$ Zu jedem $e > 0$ gibt es ein $N(e) (- N$ mit $|a - a |< e n m$ , falls $n$ , $m$ $> N (e)$ . $<==>$ $|a - a |< e n m$ für alle $n > m > N(e)$ .

Beweis als Übung:

1.Schritt:
$(an)$ ist beschränkt. Es gilt $|an -aN(e)|< e$ für $n > N (e)$ . Anwendung der Dreiecksungleichung führt auf $|an|< e + a(e)$ .
2.Schritt:
$H$ ist Häufungspunkt. Es gibt eine Teilfolge $(ank)k$ mit $(ank)k$ mit $ank '--> H$ . Ziel: $an '--> H$ für $n '--> oo$

Anwendung bei Reihen:

$sum oo ak k=0$ ist konvergent $<-->$ Zu jedem $e > 0$ gibt es ein $N (e) (- N$ mit $|sn- sm|< e$ für alle $n > m > N(e)$ .

n || sum a ||< e fur alle n > m > N (e) |k=n+1 k| ¨

Satz:

Es seien folgende Reihen konvergent mit den Grenzwerten $a$ und $b$ :

$sum oo oo sum ak = a, bk = b. k=0 k=0$

Addiert man die beiden Reihe, so addieren sich auch die Grenzwerte:

$sum oo (ak± bk) = a± b k=0$ ,

Bei Multiplikation der Reihe mit einer Konstante $c$ , wird auch der Grenzwert mit dieser Konstante multipliziert:

$sum oo ( sum oo ) cak = ca = c ak k=0 k=0$

$(zk)$ sei komplexe Folge:

zk = xk + iyk mit xk = Re(zk), yk = Im(zk)

zk '--> z(k '--> oo ) <--> xk '--> Re(z);yk '--> Im(z)(k '--> oo ) x y

2 2 2 |zk- z| = |xk- x| + |yk -y|

Zu Satz 1:

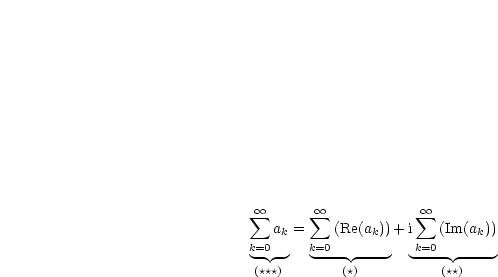
sum oo oo sum sum oo ak = (Re(ak))+ i (Im(ak)) k=0- k=0-- ---- k=0- ---- (***) (*) (**)

Falls $(*)$ und $(**)$ konvergieren, dann konvergiert $(***)$ und es gilt die Gleichheit.

Definition:

Die Reihe $sum oo ak k=0$ heißt absolut konvergent, falls die Reihe $sum oo |ak| k=0$ konvergiert.

$oo sum (-1)k--1-- k=0 k +1$ ist konvergent, aber nicht absolut konvergent, da $oo sum --1-- k=0k + 1$ divergiert. Wenn $sum ak$ konvergiert, so folgt daraus nicht, daß $sum ak$ absolut konvergent ist.

Satz:

Wenn $oo sum |ak| k=0$ konvergiert, dann konvergiert auch $oo sum ak k=0$ .

sum n sum oo ~sn = |ak|,sn = ak k=0 k=0

Zu $e > 0$ gibt es ein $N (e) (- N$ derart, daß $n sum |ak|< e k=m+1$ gilt für $n > m > N (e)$ (Voraussetzung). Es sei $e > 0$ : Wähle $N (e)$ wie oben:

n n |s - s |= || sum a ||< sum |a |< e fur n > m > N (e) n m |k=m+1 k| k=m+1 k ¨

Dies ist so nach der Dreiecksungleichung.

Bemerkungen:

Ist $oo sum k=0$ konvergent, so erhält man durch Klammersetzen wieder eine konvergente Reihe mit demselben Wert. $a = a0 + a1 + (a2 + a3)+ (a4 +-a5 +-a6)+ (a7-+-a8 + a9 +-a10)+... ~a2 ~a3 ~a4$

$sum oo ~ak = ~a0 + ~a1 + ~a3 + ~a4 +... k=0$

$~s0 = s0,~s1 = s1,~s2 = s3,~s3 = s6,~s4 = s10$
$(~s) n$ ist Teilfolge von $(s ) n$ . $~s n$ $'-->$ $a$ für $n '--> oo$ , da Teilfolgen von $(s ) n$ .
Es ist im allgemeinen nicht erlaubt, in einer unendlichen Reihe, Klammern wegzulassen oder zu versetzen. (Assoziativität) ohne den Wert der Reihe oder das Konvergenzverhalten zu verändern.
Beispiel:
$(1- 1)+ (1---1)+(1--1)+ ...= 0 0 0 0$

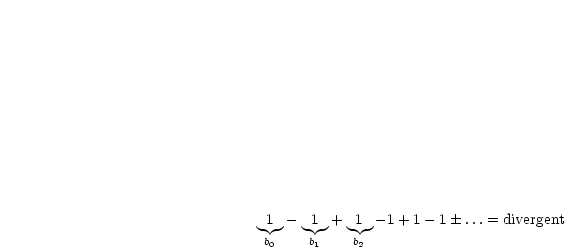
$1 - 1 + 1 -1 + 1- 1± ...= divergent b0 b1 b2$

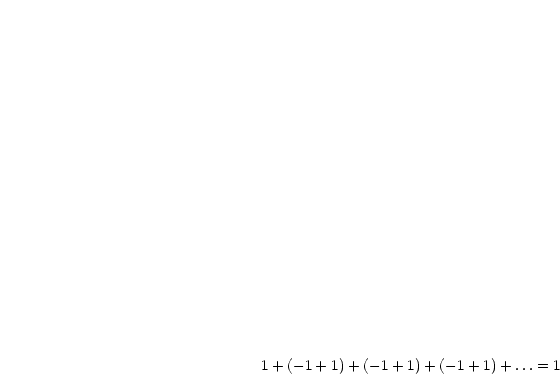
$1+ (-1+ 1) +(- 1+ 1)+ (-1 +1) +...= 1$
Umordnen der Summanden einer Reihe verändert im allgemeinen den Wert oder das Konvergenzverhalten.
(Umordnung bedeutet häufig Unordnung.)

Beispiel:
$s = 1- 1 + 1 - 1+ 1 - 1 + 1 - 1+ 1 - -1 + 1-± ... 2 3 4 5 6 7 8 9 10 11$

$1 1 1 1 1 1- 2 s = 0+ 2 + 0- 4 + 0+ 6 + 0- 8 + 0+ 10 + 0...$

$3 1 2 1 1 1 1 1 1 -s = 1+ - - -+ -+ - - - + -+ --- - ... 2 3 2 5 7 4 9 11 6$

Satz (ohne Beweis):

$sum oo ak = a k=0$ sei eine absolut konvergierende Reihe. Dann konvergiert jede Umordnung gegen denselben Wert. $( ) sum a nennt man die s-Umordnung. s(k)$