|
Es sei die Folge
|
|
Es sei die Folge
|

Die alternierende harmonische Reihe ist somit konvergent.


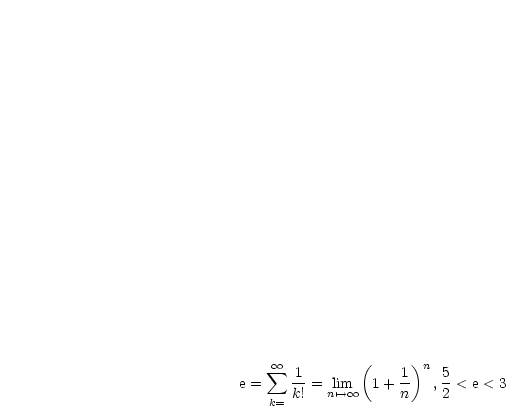



Die letzte Reihe ist bestimmt divergent.
|
|
|
|
|
|
Für die Folge |
|
|
|
|
|
|
|
Aus |
|

Es gilt  und
und  ; damit ist
; damit ist  monoton steigend
und
monoton steigend
und  monoton fallend. Somit ist
monoton fallend. Somit ist  erfüllt und es ergibt
sich
erfüllt und es ergibt
sich  für
für  . Daraus folgt der angegeben
Satz:
. Daraus folgt der angegeben
Satz:
Gilt  für für  , 1, 2, , 1, 2,  , so gilt , so gilt  . . |
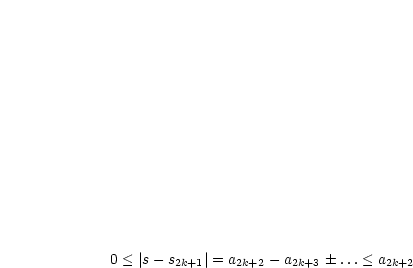 |
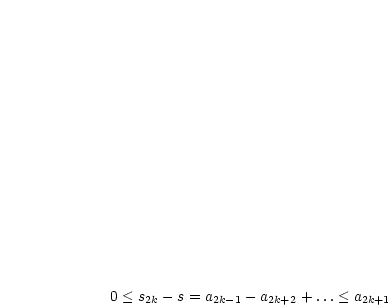 |
 |