[next] [prev] [prev-tail] [tail] [up]

Kapitel 7
Elementare Funktionen


 7.1 Die allgemeine Exponentialfunktion
 7.2 Die Hyperbelfunktionen
  7.2.1 Die reelle Hyperbolikusfunktion
  7.2.2 Umkehrfunktionen der Hyperbolikusfunktionen
 7.3 Die komplexe Exponentialfunktion
  7.3.1 Additionstheoreme
  7.3.2 Definition der Zahl p
Die Exponentialfunktion:

Die EULERsche Zahl e kann entweder durch den Grenzwert einer Folge oder der Reihe für die Exponentialfunktion dargestellt werden:

( 1 )n sum n 1 oo sum 1 e = nli'-->m oo 1+ n- = lnim'--> oo k! = k! k=0 k=0

Die Reihenentwicklung für die Exponentialfunktion lautet:

oo sum zk 1 1 1 exp(z) = k!,ak = k!,lim sup k V~ k!-= 0,r = lim-sup- V~ 1 = oo k=0 kk!

Damit kann man also die Reihenentwicklungen aller auf der Exponentialfunktion basierenden Funktionen angeben, wie beispielsweise:

4 e-x2 = 1- x2 + x ± ... 2!

Mittels dieser hilfreichen Entwicklungen lassen sich auch manche Grenzwerte elegant berechnen:

Beispiel:
-x2 2 x4± ... ( ) lim e-----14+-x--= lim 2!-4---= -1 lim x2... = 1 x'-->0 x x'-->0 x 2!x'-->0 2

Beispiel:

Es sei gegeben:

|-------(-(----1-)------)---------------2| |cn = n . f 2+ -- -f (2) mit f(x) = e4-x| ---------------n--------------------------

Den Grenzwert berechnen wir mittels einer Potenzreihenentwicklung der Exponentialfunktion:

oo sum ex = 1-xk = 1 + x+ 1x2 + ... k=0k! 2

2 ( ) 1( )2 e4- x = 1+ 4- x2 + - 4- x2 + ... 2

Damit gilt nun:

( ( ( ) ) ) ( ) 1- 2 4- 1- g = nli'-->mo o cn = nli'-->m oo n . 1 + 4- 2+ n + ...- 1 = n . 4 - 4- n - n2 = ( ) |--| = lim n. -4-- -12 = lim -4- 1-= --4- n'-->o o n n n'-->o o n
(7.1)

exp(0) = 1 = e0,exp(1) = e = e1

Das Additionstheorem für die Exponentialfunktion lautet:

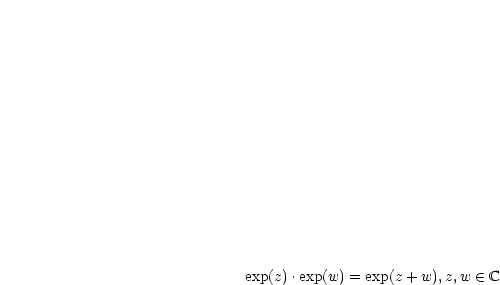
exp(z).exp(w) = exp(z + w),z,w (- C

Des weiteren gelten folgende Rechenregeln:

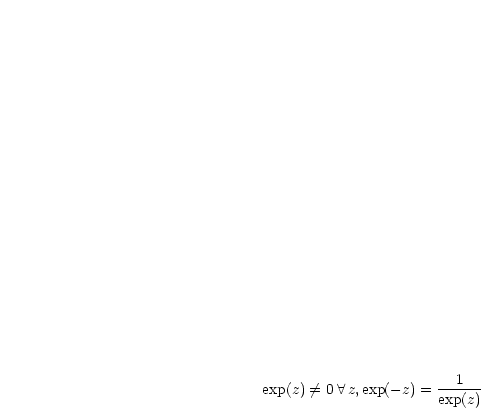
--1--- exp(z) /= 0 A z,exp(-z) = exp(z)

exp(n) = en,n (- Z

V~ --------- exp(r) = er,r (- Q, emn-= n e.e.....e m

exp(mz) = exp(z + z + z + ...+ z) = (exp(z))m ,m (- N ------ m------

Dies kann man durch vollständige Induktion zeigen.

( ) [ ( )]m r = n-mit n,m (- N : er = exp(r) = exp m .n = exp m- m m n

V~ n- n- (n ) en = e m = exp m-

( )n -n ( n-) ( ( 1-)) [ ( -1)]n ---1--- (-1-)n --1n r = m : exp - m = exp n + - m = exp -m = exp(1 ) - em1 = e m n

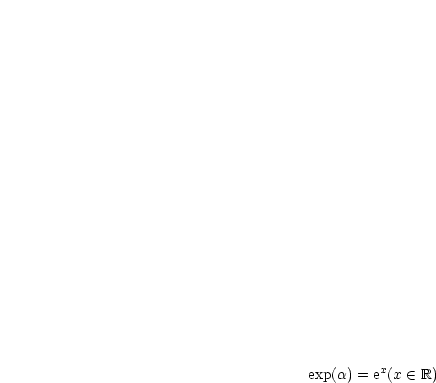
x exp(a) = e(x (- R)

Es sei x (- R . Wähle (rn) , rn (- Q mit rn '--> x für n '--> oo .

rn e = exp(rn) '--> exp(x)(n '--> oo )

Die Exponentialfunktion ist stetig und bijektiv (injektiv und surjektiv). Für komplexe Zahlen z gilt:

z x iy e = exp(z) = exp(x + iy) = exp(x)exp(iy) = ee

Für x (- R ist f(x) = ex streng monoton wachsend und ex > 0 .

Grenzwerte:
x lim -e-= oo , lim xke-x = 0,k (- N U {0} x'--> oo xk x'--> oo

Zum Beweis führen wir folgende Abschätzung durch:

x x2 x3 xk xk+1 xk+1 e = 1+ x+ 2! + 3! + ...+ k! + (k-+1)! + ...> (k+-1)! f¨ur x > 0

Wir bringen diesen Ausdruck auf die gewünschte Form:

xk+1 ex x ex > (k-+1)!,xk-> (k+-1)!

Die Exponentialfunktion geht somit schneller gegen unendlich als jede noch so große Potenz von x .

Injektivität:

Die Funktion ist injektiv, da sie streng monoton wachsend ist.

Surjektivität:

Gegeben ist a (- (0, oo ) . Gesucht ist x (- R mit ex = a . Wir argumentieren mit Stetigkeit: lxim'--> oo ex = 0 , xli'-->m oo ex = oo und mit dem Zwischenwertsatz: Da exp:R '--> (0, oo ) bijektiv ist, gibt es eine Funktion exp-1 =: ln . Dabei handelt es sich um den natürlichen Logarithmus, der das Intervall (0, oo ) auf R abbildet.

ex = y <==> x = lny

Die ln -Funktion ist stetig und streng monoton wachsend.

eln y = y f¨ur y > 0

ln(ex) = x, x (- R

ln(e) = 1, ln1 = 0 ==> ln x < 0 f¨ur 0 < y < 1

xl'-->im0+ lnx = - oo , xli'-->mo o lnx = oo

Satz:

  • ln(x,y) = ln(x)+ ln(y) , ln 1-= - ln x x für x , y > 0
  • xli'-->m oo x-k ln x = 0 , lim xk ln x = 0 x'-->0+ für k = 1 , 2, ...

Beweis:

[next] [prev] [prev-tail] [front] [up]