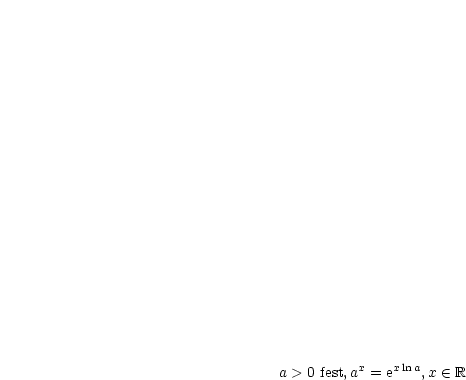
Für die allgemeine Exponentialfunktion und ihre Umkehrfunktion, dem Logarithmus, gelten folgende Regeln:
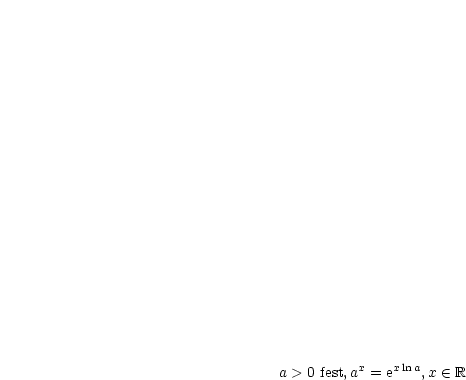






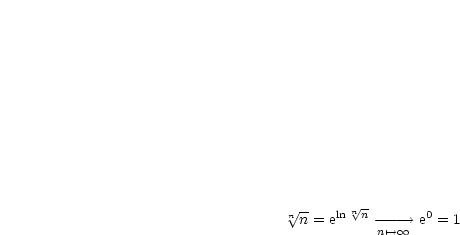
Es sei  . Dann gilt:
. Dann gilt:


Für die Reihenentwicklung von  ergibt sich mittels der Entwicklung für die
Exponentialfunktion:
ergibt sich mittels der Entwicklung für die
Exponentialfunktion:

Damit können wir beispielsweise folgenden Grenzwert berechnen:



 ist die zugehörige Umkehrfunktion
ist die zugehörige Umkehrfunktion  . Für diese
Umkehrfunktion gilt:
. Für diese
Umkehrfunktion gilt:
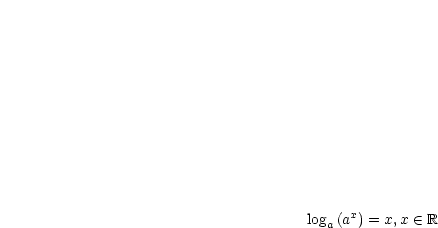

 ,
,  :
:
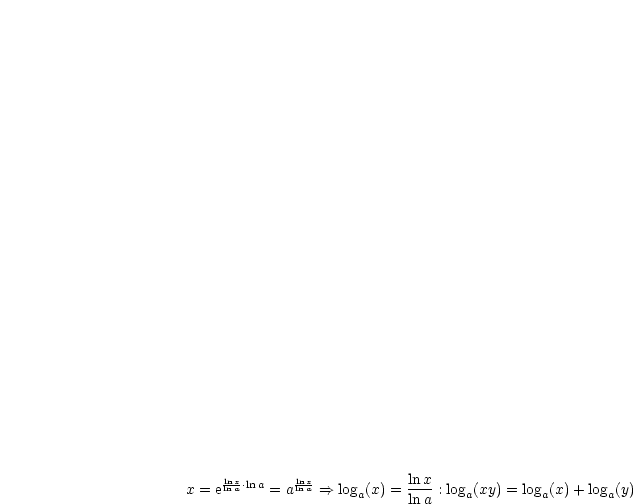
 ,
,  :
:  ,
, 
