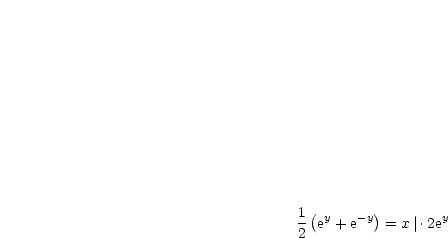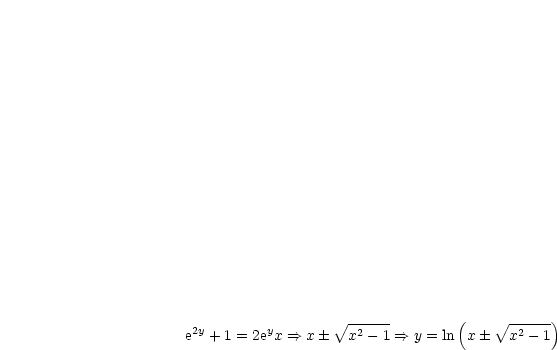7.2 Die Hyperbelfunktionen

Es sei $z (- C$ . Dann werden folgende Funktionen definiert:

Kosinushyperbolikus: $cosh(z) = 1(ez + e-z) 2$
Sinushyperbolikus: $sinh(z) = 1(ez- e-z) 2$
Tangenshyperbolikus: $z -z tanh(z) = e---e- ez + e-z$

Die Reihenentwicklung des Kosinushyperbolikus folgt mittels der Reihen der Exponentialfunktion:

( oo sum k sum oo k) sum oo sum oo 2k 2 4 cosh(z) = 1 z-+ (-1)kz- = 1 (1+ (- 1)k)1-zk = -z---= 1+ z-+z- +... 2 k=0 k! k=0 k! 2k=0 k! k=0(2k)! 2! 4!

Die ungeraden Koeffizienten sind gleich Null, die geraden gleich $-1--- (2k)!$ :

1 a2k+1 = 0,a2k =----- (2k)!

Der Konvergenzradius ist gleich unendlich:

r = -----1 V~ ----= oo limsup k |ak|

Für die Reihenentwicklung des Sinushyperbolikus ergibt sich:

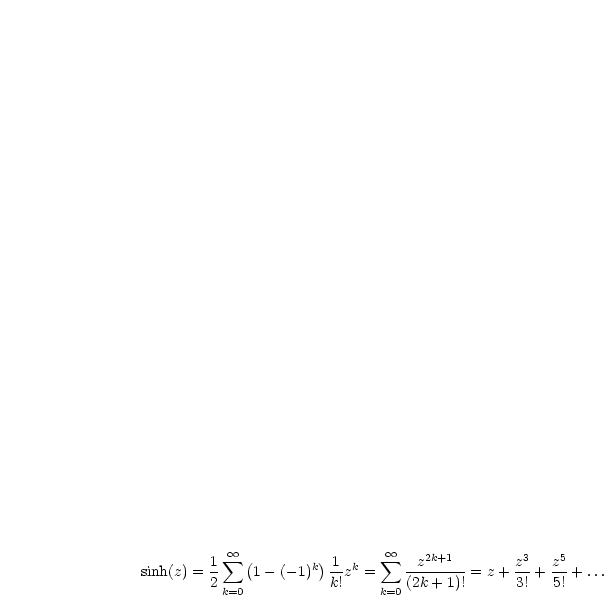
oo oo 1 sum ( k)1- k sum -z2k+1-- z3 z5 sinh(z) = 2 1- (-1) k!z = (2k+ 1)! = z + 3! + 5! +... k=0 k=0

$cosh(z)$ ist achsensymmetrisch zur $y$ -Achse

cosh(z) = cosh(- z),cosh(0) = 1

$sin(z)$ ist punktsymmetrisch zum Ursprung:

sinh(z) = - sinh(- z),sinh(0) = 0

z = x (- R : cosh(x) > 1 A x

Satz:

$cosh(z + w) = cosh(z)cosh(w) + sinh(z)sinh(w) sinh(z + w) = sinh(z)cosh(w)+ cosh(z)sinh(w)$ für $x$ , $w (- C$

$cosh2(z)- sinh2(z) = 1$ , $(x2- y2 = 1)$

Setze oben $w = -z$ : $1 = cosh(0) = cosh(z)cosh(- z)+ sinh(z)sinh(- z) = cosh2(z)- sinh2(z)$

Übung:

ez+w = ezew und Definition

Wo kommt der Name Hyperbelfunktion her?

7.2.1 Die reelle Hyperbolikusfunktion

Satz:

$y = sinh(x)$ ist streng monoton wachsend.
$y = cosh(x)$ ist streng monoton wachsend auf $[0, oo )$ und streng monoton fallend auf $(- oo ,0]$ .
$y = tanh(x)$ ist streng monoton wachsend.

Begründungen:

Begründung zu a.) $sinh(x) = 1(ex- e-x) 2$

$ex ist monoton wachsend { } -1 = e-x ist monoton fallend 1(ex- e-x) ist streng monoton wachsend ex 2 -x - e ist monoton wachsend$
Begründung zu b.)
$cosh(x2)- cosh(x1) = cosh(x2)--cosh(x1).(cosh (x2)+ cosh(x1)) = cosh(x2)+ cosh(x1) cosh2(x2)- cosh2 (x1) 1+ sin2(x2)- 1- sin2(x1) = -cosh(x2)+-cosh-(x1)- = ---cosh-(x2)+-cosh-(x1)--- = 2 2 = -sin-(x2)--sin--(x1)-> 0 cosh(x2)+ cosh(x1)$ (7.2)

Dieser Ausdruck ist für $x2 > x1 > 0$ offenbar auch größer 0, was aus der Monotonie des Sinushyperbolikus folgt. Damit haben wir die Monotonie des Kosinushyperbolikus auf dem Intervall $[0; oo ]$ gezeigt. • Begründung zu c.)
$ex---e-x- --2e--x-- ---2-- tanh(x) = ex + e-x = 1 - ex + e-x = 1- 1 + e2x$

$2x 1 1 1+e ist monoton wachsend, 1+-e2x ist monoton fallend, daher ist- 1+-e2x monoton wachsend$

Des weiteren gilt:
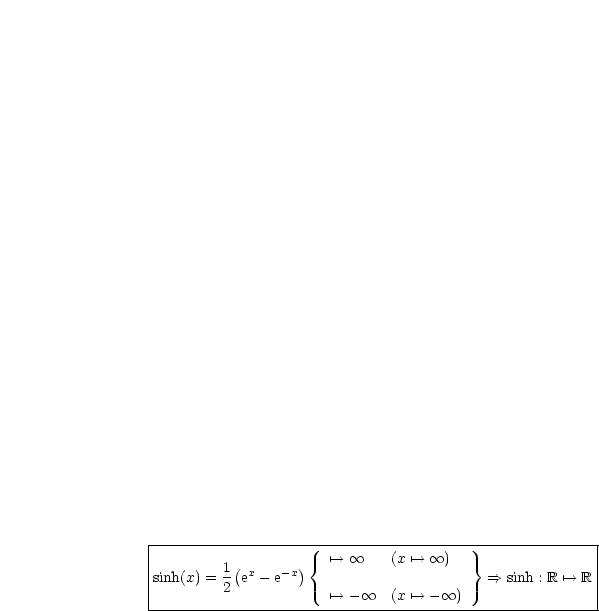
$|--------------------------------------------------------| | 1( x -x){ '--> oo (x '--> oo ) } | |sinh(x) = 2 e - e ==> sinh : R '--> R| -----------------------'-->--- oo --(x '-->-- oo )-----------------|$

$|------------1-(-------)---------------| |1 < cosh(x) = ex + e-x '--> oo f¨ur x '--> oo -------------2-------------------------|$
Der Kosinushyperbolikus bildet $R$ auf das Intervall $[1, oo )$ ab.
$|-----------------------x--------------| -0-<-cosh(x)--sinh(x)-=-e--'-->--0 f¨ur x-'-->- oo$
Also nähern sich der Sinus- und Kosinushyperbolikus für $x '--> oo$ beliebig. Darüber hinaus betrachten wir den Tangenshyperbolikus:
$|--------------------------------------| | 2 { '--> 1 (x '--> oo ) | tanh(x) = 1 - 1+-e2x | ----------------------'-->---1--(x-'-->--- oo )--$

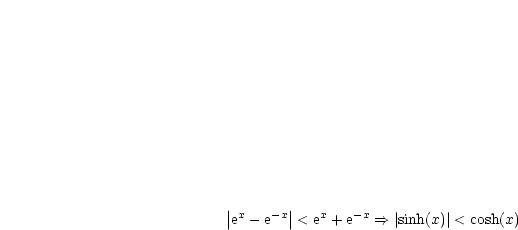
$||ex- e-x||< ex + e-x ==> |sinh(x)|< cosh(x)$

$|------------------------| |||e+x- e-x|| | |||e+x +-e-x||= |tanh(x)| < 1 -------------------------$

7.2.2 Umkehrfunktionen der Hyperbolikusfunktionen
$sinh : R <--> R : sinh-1(x) = arsinh(x)$
Die Umkehrfunktion nennen wir den Areasinushyperbolikus. Die Verknüpfung dieser beiden Abbildungen ergibt gerade wieder die Identität:
$|----------------------------------| |arsinh(sinh(x)) = x,sinh (arsinh(x)) = x ------------------------------------$

$y = cosh(x) : [0, oo ) '--> [1, oo ) : y = arcosh(x)$

$y = cosh(x) : (- oo , 0] '--> [1, oo ) : y = arcosh(x)$
Die Umkehrfunktion heißt Areakosinushyperbolikus. Auch für sie gilt:
$|--------------------------------| |arcosh (cosh(x)) = x,cosh (arcosh(x))| ---------------------------------$
Wir leiten den expliziten Ausdruck für den Areakosinushyperbolikus her. Dazu lösen wir $cosh(y) = x$ nach $y$ auf und erhalten:
$1 (ey + e-y)= x |.2ey 2$

$2y y V~ -2---- ( V~ -2---) e + 1 = 2e x ==> x ± x - 1 ==> y = ln x ± x - 1$

$|-----(---- V~ -----)------------| |y = ln x + x2- 1 = arcosh+(x)| --------------------------------$

$|-----(---- V~ -----)------------| |y = ln x - x2- 1 = arcosh-(x)| --------------------------------$

$V~ ----- x > 1 <--> 0 < x - x2 - 1 < 1$

[next] [prev] [prev-tail] [front] [up]