7.3 Die komplexe Exponentialfunktion

Satz:

Für die komplex konjugierte Exponentialfunktion gilt:

$------ exp(z) = exp(z)$ , $z (- C$

Beweis:

Wir können die Exponentialfunktion als unendliche Reihe schreiben:

n sum zk exp(z) = nli'-->mo o k! k=0sn(z)

Hier ist dann ersichtlich, daß für die Partialsummen $sn(z)$ gilt:

----- lim Sn(z) = Sn(z) n'-->o o

Daraus folgt also:

exp(z)-= exp(z)

$z$ sei eine komplexe Zahl mit $Im(z) = 0$ . Dann gilt:

z = ix,x (- R,z = -ix,eix = eix = e-ix

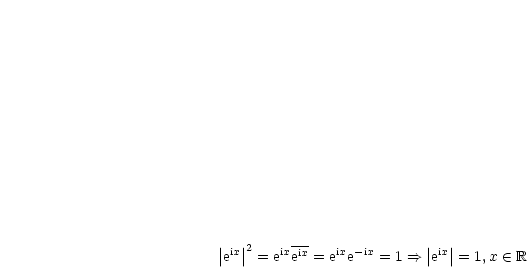
--- ||eix||2 = eixeix = eixe-ix = 1 ==> ||eix||= 1,x (- R

( ) arg eix = x

An dieser Stelle muß man jedoch aufpassen:

| | | | | | | | | || | |eiz|= ||ei(x+iy)||= ||eix-y)|| = |eixe-y|= |eix||e-y|= e-y

Nun gilt ja:

i2k = (-1)k,i2k+1 = i(- 1)k

Wir wollen nun eine Beziehung zwischen der komplexen Exponentialfunktion und dem reellen Sinus und Kosinus herleiten. $eiz$ konvergiert absolut für alle $z$ :

iz sum oo -1 kk -1 2 1- 3 e = k!i z = 1+ iz- 2!z + i3!z ... k= oo 0 oo = sum --1-i2ke2k + sum ---1---i2k+1z2k+1 = k=0(2k)! k=0 (2k+ 1)! sum oo oo sum = --1--(-1)kz2k+ i ---1---(- 1)kz2k+1= cosz + isinz k=0(2k)! k=0 (2k+ 1)! -----cos(z)------ -------isin(z)-------

(7.3)

|------------------------| |eiz = cosz + isinz f¨ur z (- C| -------------------------

Damit haben wir nun die Reihendarstellung des Sinus und des Kosinus erhalten:

|------------------------------------------------------| | oo sum z2k z2 z4 | cosz = (-1)k(2k)! = 1- 2-+ 4! + ... f¨ur z (- C mit r = oo -------k=0----------------------------------------------

Daraus ist dann ersichtlich:

|---------------| | cosz- 1 | cosz = cos(-z),cos(0) = 1,|lz'-->imo o -z----= 0| -----------------

|----------------------------------------------------------| | sum oo k z2k+1 z3 z5 | |sin z = (-1) (2k-+-1)! = z- 3! + 5!± ... f¨ur z (- C mit r = oo -------k=0-------------------------------------------------

Aus hier sieht man:

|-----------| | sinz | sin z = - sin(- z),sin 0 = 0,-liz'-->m0-z--=-1-

( ) eiz n = (cosz + isinz)n

An dieser Stelle kann man nun viele hilfreiche Beziehungen herleiten:

|---------------------| einz = cos(nz)+ isin(nz) | -----------------------

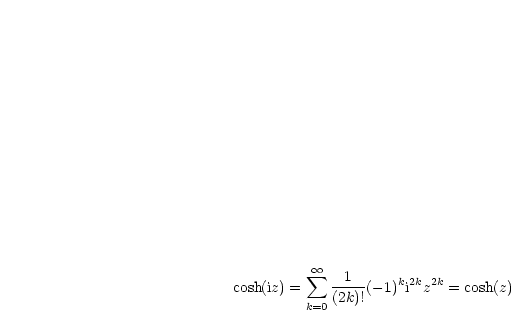
sum oo 1 cosh(iz) = ----(-1)ki2kz2k = cosh(z) k=0 (2k)!

oo sum ---1---- k2k+1 2k+1 sinh(iz) = (2k+ 1)! (-1) i- z = isinh(z) k=0 i

|-----------------------------| cosz-=-cosh(iz),sin-z =---isinh(iz)|

Des weiteren ergeben sich durch Variablentransformation $z '--> iz$ in den Potenzreihen von Sinus und Kosinus folgende wichtige Beziehungen, die vor allem in der Funktionentheorie (HM III) große Bedeutung haben:

1( iz -iz) 1( iz -iz) -1( iz -iz) cosz = 2 e + e ,sin z = - i2 e - e = 2i e - e

|------1(--------)--------1-(-------)-------| cosz = - eiz + e-iz ,sin z =--eiz- e-iz ,z (- C| -------2------------------2i-----------------|

|----------------------------| |cosx = 1(eix + e-ix)= Re(eix) | --------2--------------------|

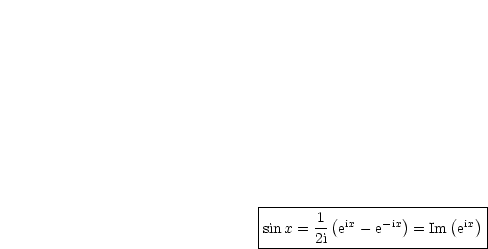
|----------------------------| | -1( ix -ix) ( ix) | |sin x = 2i e - e = Im e | -----------------------------

7.3.1 Additionstheoreme

Satz:

Für $sin(z)$ und $cos(z)$ gelten folgende Additionstheoreme:

$sin(z + w) = sinzcosw + coszsin w$
$cos(z + w) = cosz cos w- sinzsinw$
$z + w z -w cosz- cosw = 2sin --2--sin--2--$

Beweis:

Wir wollen nur das erste Additionstheorem beweisen. Die anderen beiden sollen als Übung durchgeführt werden:

[( )( ) ( )( )] sinz cosw+ coszsinw = -1 eiz - e- iz eiw + e-iw + eiz + e-iz eiw- e-iw 4i[ ] [ ] = -1 2ei(z+w)- 2ei(z+w) = -1 ei(z+w)- e-i(z+w) = sin(z + w) 4i 2i

(7.4)

7.3.2 Definition der Zahl $p$

Wir betrachten den Kosinus auf dem Intervall $[0,2]$ . $cos(x)$ hat dort genau eine Nullstelle.

$cosx$ ist auf dem Intervall streng monoton fallend.
Für $x2 > x1$ gilt also, daß $cos x2 < cosx1$ .
$cos0 = 1$ , $1 cos2 < - 3$
$sinx$ ist $> 0$ in $[0,2]$ .

Wir betrachten nun die Potenzreihen des Kosinus und des Sinus:

Kosinus: $sum oo k z2k-- z2 z4 cosz = (- 1) (2k)! = 1- 2 + 4! + ... f¨ur z (- C k=0$
Wir zeigen, daß die Reihe von $cos 2$ konvergiert:
$ak > ak+1$

$22k ak = -----'--> 0 f¨ur k '--> oo (2k)!$
Damit stellt $(ak)$ eine Nullfolge dar, die notwendige Bedingung für Konvergenz ist erfüllt. Nun gilt außerdem nach dem Quotientenkriterium:
$ak+1 ------22------ ak = (2k+ 2)(2k+ 1) '--> 0 f¨ur k '--> oo$
Damit konvergiert als $cos2$ . Wir setzen nun den Wert 2 ein und erhalten dann folgende Abschätzung für $cos2$ :
$s1 oo sum 2k --- --2 4 s = cos2 = (- 1)k-2---= 1 - 2-+ 2-± ...< s2 = - 1+ 2 = - 1 k=0 --- (2k)! s0 2! 4! 3 3 ak ----- ----- s2$
Damit folgt für die Monotonie auf dem Intervall $[0,2]$ :
$>0 >0 x-+ x- x----x 0 < x1 < x2 < 2,cos x2- cosx1 = - 2sin-1--2-sin--2---1< 0 --2 -- --2-- (- [0,2] <2$
Sinus: $oo sum z2k+1 z3 z5 sinz = (-1)k(2k+-1)! = z - 3! +-5!± ... f¨ur z (- C mit r = oo k=0$
Wir wollen zeigen, daß nachfolgende Glieder der Folge $(an)$ größer sind als vorhergehende:
$x2k+1 0 < ak = (2k-+-1)!$

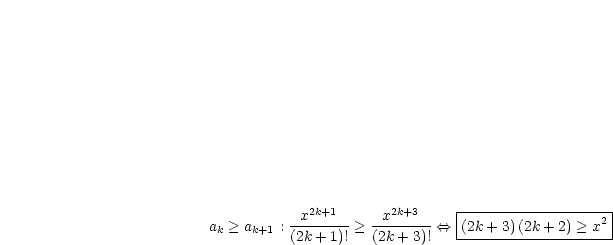
$--x2k+1-- -x2k+3-- |-----------------2-| ak > ak+1 :(2k+ 1)! > (2k + 3)! <==> -(2k-+-3)(2k-+-2) >-x-|$
Diese letzte Beziehung gilt sicher, falls $6 > x2$ .
$2 2 0 < x < 2 : x < 4,- x > - 4$
Außerdem stellt $(ak)$ eine Nullfolge dar:
$x2k+1 ak = (2k+-1)! '--> 0 f¨ur k '--> oo und 0 < x < 2$
Für $0 < x < 2$ gilt somit:
$s1 oo --- --- s = sinx = sum (- 1)k-z2k+1-= x - x3+ x5± ...> s k=0 (2k+ 1)! 3! 5! 1 s0$

Satz:

$y = cos x$ hat im Intervall $(0,2)$ genau eine Nullstelle $x0$ .

Definition:

Die Zahl $p$ wird nun definiert als doppelte Nullstelle des Kosinus im Intervall $[0;2]$ : $p = 2x0$

Dabei gilt für $p$ folgende Abschätzung: $0 < p < 4$

\text{[math]}

Außerdem folgt:

p p p p sin22-+ cos2 2-= 1 = sin2 2-==> sin 2-= 1

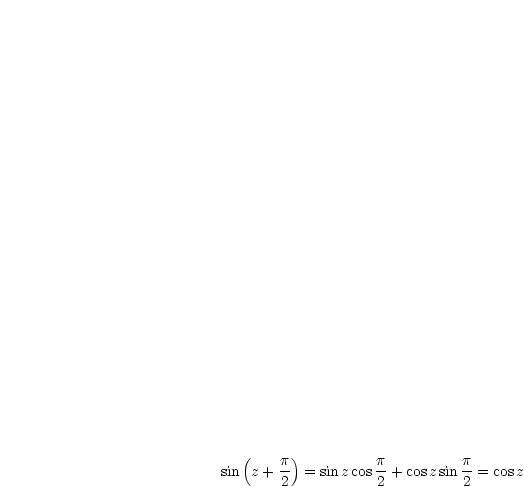
( p) p p sin z + -- = sin zcos--+ coszsin --= cosz 2 2 2

Satz:

Folgende wichtige Werte gelten für die komplexe Exponentialfunktion:

$e±ip2 = ±i$ , $e±ip = - 1$ , $ei3p2 = -i,ei2p = 1$ , $ei2kp = 1$ für $k (- Z$

$eipk = (-1)k$ für $k (- Z$ , $ei(2k+1)p2 = i(-1)k$ für $k (- Z$

Beweis:

Zum Beweis verwenden wir die EULERsche Formel und unsere Kenntnisse über $p$ :

eix = cosx + isinx(x (- R)

+ip -ip 1 ±ip ( ip )2 i3p- ip+ p e 2 = i,e 2 =-i = - i,e = e2 = -1,e 2 = e 2 = - i

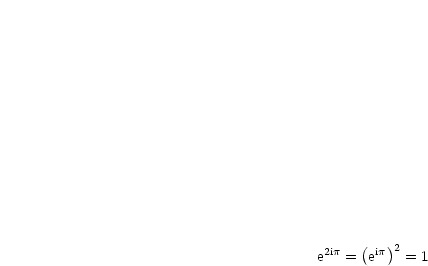
e2ip = (eip)2 = 1

ei2kp = (ei2p)k = 1

ei(2k+1)p2 = eipkeip2 = i(- 1)k

Hier folgt nun eine Tabelle der wichtigsten Werte:

|| | | | | | | ||0| p-| p | 3p--|2p | kp |(2k + 1)p- sinx ||0| 21 | 0 |-21 |0 | 0 | (- 1)k 2 cosx ||1| 0 |-1 | 0 |1 |(-1)k | 0 || | | | | | |

Periodizität:

y = cosx } [ p] y = sin x sind bekannt, wenn y = cosx auf 0,2 bekannt.

( p-) cosx = sin x+ 2

$cosx$ ist gerade. Auf $[- p, p-] 2 2$ ist $cosx$ bekannt.
$sinx$ ist auf $[0,p]$ bekannt, $cosx$ ist verschoben. $sin x$ ist somit auf $[-p,+p]$ ungerade.
$cosx$ , $sinx$ sind auf Intervall der Länge $2p$ bekannt, wegen der $2p$ -Periodizität sind also $cosx$ , $sin x$ überall bekannt. Diese folgt aus der $2p$ -Periodizität der komplexen Exponentialfunktion: $e2pi = ez .1 = ez+2pi$

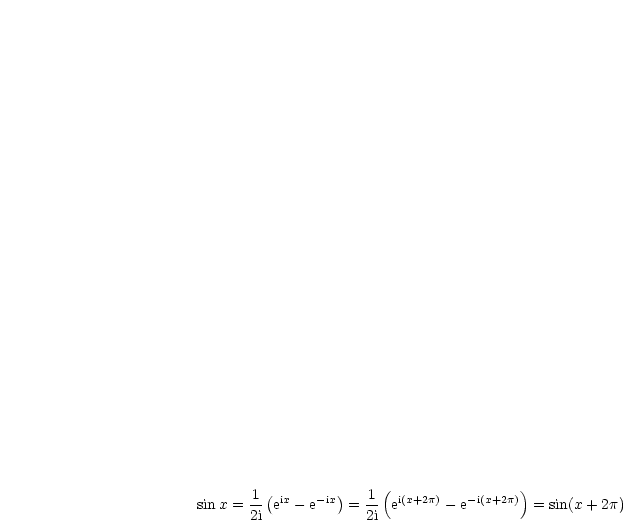
$1( ) 1 ( ) sinx = 2i eix - e-ix = 2i ei(x+2p)- e- i(x+2p) = sin(x+ 2p)$

$|--------------------------------| e2pi =-ez+2pi-und-sin(x) =-sin(x-+-2p)$

Übung:

Man zeige, daß $tan x$ und $cotx$ $p$ -periodisch sind.

Monotonie:

Wir fassen unsere Erkenntnisse über die Monotonie der trigonometrischen Funktionen und deren Umkehrfunktionen zusammen:

Sinus:
$sinx$ ist auf jedem Intervall $[ ] [ ] -p-+ kp, p-+ kp = (2k - 1)p-,(2k + 1)p- 2 2 2 2$ streng monoton für $k (- Z$ .
Kosinus:
$cosx$ ist auf jedem Intervall $[0 + kp,p+ kp] = [kp,(k+ 1)p]$ streng monoton.
Arkussinus: $[ p p] v '--> u := arcsink(v) f¨ur v (- [- 1,+1] <==> sinu = v mit u (- (2k -1)2-,(2k + 1)2$
Den Teil für $k = 0$ nennen wir den Hauptzweig des Arkussinus:
$[ p p ] u = arcsin0(v) = Arcsin(v) mit u (- +-2,+-2$

$[ p- p] arcsink (sin(u)) = u,u (- (2k- 1)2,(2k+ 1)2$

$sin (arcsink(v)) = v,v (- [-1,+1]$
Arkuskosinus: $u = arccosk(v),v (- [-1,+1] <==> cosu = v,u (- [kp,(k +1)p]$
Für $k = 0$ folgt wiederum der Hauptzweig des Arkuskosinus:
$u = arccos0(v) = Arccos(v)$

Bemerkung:

Im folgenden sprechen wir nur von den Hauptzweigen des Arkussinus und Arkuskosinus und bezeichnen diese mit $arcsin(x)$ und $arccos(x)$ .

Satz:

Für die komplexe Exponentialfunktion gilt folgende Gleichung:

$ez = 1 <==> z = 2kpi fur k (- Z ¨$

\text{[math]}

Die in der Mathematik sehr bedeutenden Zahlen, nämlich die Eulersche Zahl e, die Kreiszahl $p$ und die imaginäre Einheit i sind somit in einer einzigen Gleichung miteinander verknüpft, was sehr überraschen ist. Diese Gleichung hat wiederum in der Funktionentheorie (HM III) eine sehr wichtige Bedeutung.

Beweis:

„ $<==$ stimmt nach Satz 2.

„ $==>$ $ez = 1$

Wir suchen nun $z = x+ iy$ mit $ex+iy = 1$ . Alle gesuchten $z$ haben die Form $z = iy$ .

| | | | ! |ex+iy|= |ex||eiy| = ex = 1

Mit $x = 0$ folgt somit die zu beweisende Aussage:

eiy = 1

Außerdem müssen wir noch zeigen, daß $eiy /= 1$ für $0 < y < 2p$ . Wir führen wieder einen Widerspruchsbeweis durch. Wir nehmen also an:

iy Es sei 0 < y < 2p und e = 1

Für $0 < y-< p 4 2$ folgt:

eiy4 = cos y-+isin y-= u+ iv - 4 - 4 u v

Für die komplexe Zahl $u + iv$ gilt:

u > 0,v > 0,u2 +v2 = 1

Wir potenzieren obige Gleichung mit 4 und erhalten:

( ) 1 = eiy = (u+ iv)4 = u4- 6u2v2 + v4 + i4uv-u2 --v2 =0

Durch Vergleich mit der linken Seite folgt dann, daß der Imaginärteil der komplexen Zahl 0 sein muß. Damit gilt:

u2 = v2 und somit u = v

Mit der Nebenbedingung $u2 + v2 = 1$ ergibt sich nun:

u = v = V~ 1 2

Wieder eingesetzt in die obige Gleichung ergibt:

1 3 1 1 = 4- 2 + 4 = -1

Dabei handelt es sich um einen Widerspruch. Somit ist $eiy /= 1$ für $0 < y < 2p$ .

Nullstellen von $cosh(z)$ :

Wir wollen zum Abschluß die Nullstellen von $cosh(z)$ berechnen:

1(ez + e-z)= 0 2

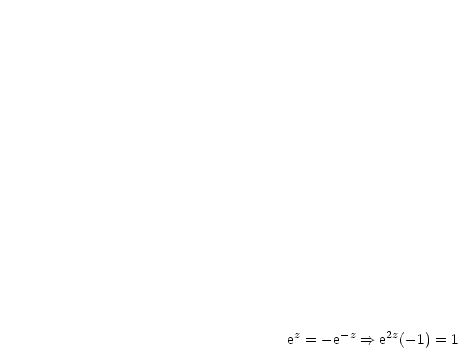
z - z 2z e = - e ==> e (-1) = 1

e2z-ip = 1

Mit der zuvor bewiesenen Beziehung $2kpi e = 1$ folgt nun:

2z-ip 2kpi e = e

Dann ergibt sich durch Logarithmieren:

2z- ip = 2kpi

------------------------------------ | 1 p | |z = 2 (2kpi + ip) = i(2k+ 1)2-f¨ur k (- Z ------------------------------------

Damit folgen die Nullstellen des Kosinus:

|----------------| cosz-=-cosh(iz) =-0

p iz = i(2k + 1)2

Daraus ergibt sich:

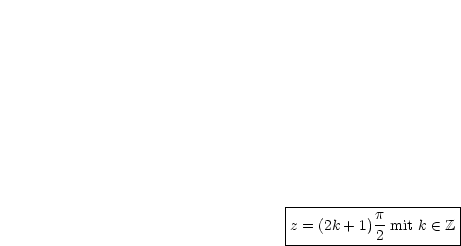
|---------------------| | p- | z-=-(2k+-1)2-mit k- (- -Z

Wir haben kennengelernt:

Die komplexe Exponentialfunktion $exp(z)$ , die reelle Exponentialfunktion $exp(x)$ und deren Umkehrfunktion $ln x$ $f(z) = ez,f(x) = ex,ln x$
Hyperbolische Funktionen, Areafunktionen (durch Logarithmus ausdrückbar)
Trigonometrische Funktionen, Arcusfunktionen $1 ( ) sinx = -- eix- e-ix 2i$