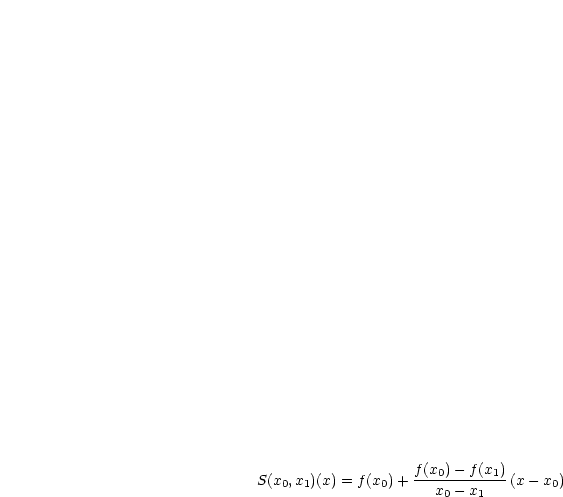


|
Falls |
|
 ist in
ist in  nicht differenzierbar, da die Ableitung nicht existiert.
nicht differenzierbar, da die Ableitung nicht existiert.

Aus Stetigkeit folgt nicht Differenzierbarkeit.
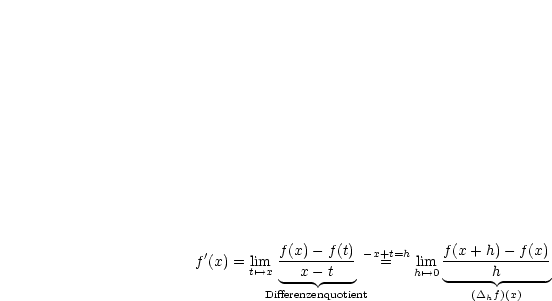
Die Zuordnung  ist eine Funktion (die Ableitung) von
ist eine Funktion (die Ableitung) von  . Der
Definitionsbereich
. Der
Definitionsbereich  existiert
existiert
 . Geht man von
. Geht man von  aus, so erhält man durch Ableiten
aus, so erhält man durch Ableiten  , nämlich die zweite
Ableitung.
, nämlich die zweite
Ableitung.


