9.4 Der Hauptsatz der Differential- und Integralrechnung

[next] [prev] [prev-tail] [tail] [up]

9.4 Der Hauptsatz der Differential- und Integralrechnung

Satz:

$f (- C0[a,b]$ , $c (- [a,b]$ sei beliebig, aber fest. Dann gelten:

Die durch $integral x Fc(x) := f(t)dt c$ , $a < x < b$ definierte Funktion $Fc$ ist Stammfunktion von $f$ . Jede andere Stammfunktion von $f$ hat die Form $Fc(x) + k$ mit $k = const.$ .
Ist $F$ Stammfunktion von $f$ , so gilt $b integral b f(x)dx = F (b)- F (a) = F (x)|x=a a$

Beweis von 1.):

x integral +h integral x x+ integral h F(x +h) - Fc(x) = f(t)dt- f(t)dt = f (t)dt = f(q)h c c x - - q (- (x,x+h)

1 hli'-->m0 --(Fc(x + h)- Fc(x)) = lih'-->m0 f(q) = f(x) = F 'c(x) h

Sei $F$ eine andere Stammfunktion:

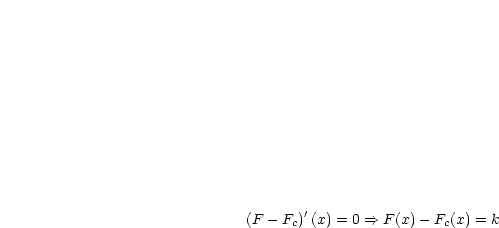
(F- Fc)'(x) = 0 ==> F(x)- Fc(x) = k

Beweis von 2.):

integral b integral b integral b F(b)-F (a) = Fc(b)+k- Fc(a)- k = Fc(b)-Fc(a) = f (t)dt- f(t)dt = f(t)dt a c a

( integral x ) D f(t)dt = f(x) c

Bemerkungen:

Es gilt also folglich:

F'(x) = f(x),a < y < b

b b x x integral integral ' integral ' integral ' f(t)dt = F(b)- F(a), F (t)dt = F(b)- F(a), F (x)dt = F (x)- F(a), F (t)dt = F(x)-F (c) a a a c

Man schreibt bei der Differentiation von Integralen:

( ) ( ) integral x d integral x Dx f(t)dt oder--- f(t)dt c dx c

Beispiel:

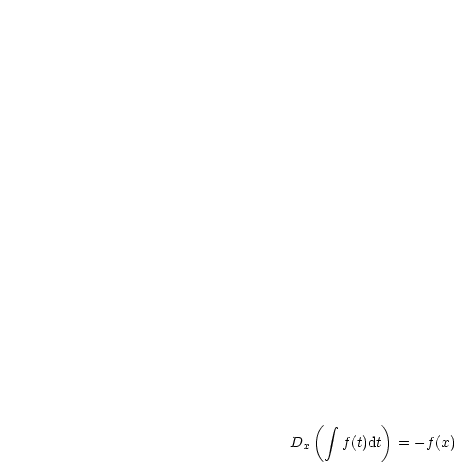
(i ntegral ) D f(t)dt = -f(x) x

9.4.1 Das unbestimmte Integral:

$integral f (x)dx$ von $f$ ist die Menge aller Stammfunktionen von $f$ .

$integral { integral x } { integral x } f (x)dx = f(t)dt+ k,k (- R = f(t)dt,c (- R c c$

Beispiel:

integral cosxdx = sin x

Für ein unbestimmtes Integral lassen wir die untere Grenze bei der Schreibweise weg:

integral x costdt = sinx

Beispiele:

integral x dt 1 ||1 + x|| ----2 = - ln||-----|| 1 -t 2 1 - x

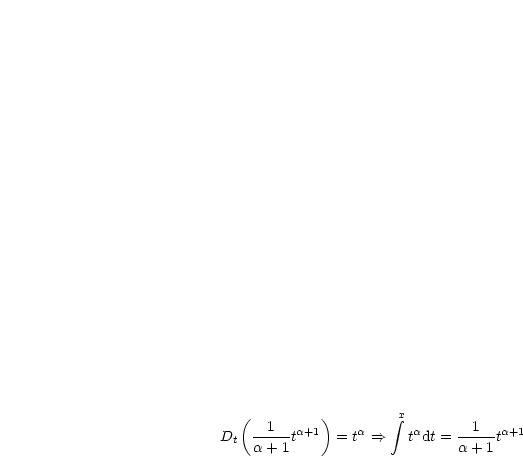
( ) integral x Dt -1--ta+1 = ta ==> tadt =--1--ta+1 a+ 1 a + 1

Für $a = - 2$ gilt somit:

x integral t- 2dt = --1 x

Doch hier ist Vorsicht geboten:

integral 2 |2 = - 1|| = -1 - 1 = - 3 ist falsch, da f bei 0 unendlich großwird. x|-1 2 2 -1

( 2 )' sin x = 2sin xcosx

( 2 )' - cos x = 2sin xcosx

( 1 )' - 2 cos2x = 2sinxcosx

In der Formelsammlung findet man beispielsweise:

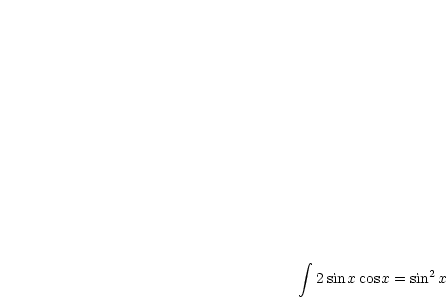
integral 2sinx cosx = sin2x

integral 2sinx cosx = - cos2x

integral 1 2 2sin xcosx = -2 cos x

/==> sin2x = - cos2x = - 1cos2x 2

Weitere Tricks:

integral x integral x f(t)f'(t)dt = 1 (f2)'(t)dt = 1f 2(x) 2 2

integral x integral x f'(t) ' f(t)dt = (ln|f(t)| ) dt = ln|f(x)|

Beispiel:

integral x integral x (cost)' tantdt = - -----dt = -ln|cost| cost

9.4.2 Wichtige Stammfunktionen:

integral x dt integral x dt V~ ---2-= arcsinx, 1-+-t2 = arctan t 1- t

Beispiel zum Hauptsatz der Differential- und Integralrechnung:

g integral (x) p(x) = h(t)dt c

Mit der Kettenregel folgt:

integral t q(t) = h(t)dt ==> q'(t) = h(t) c

p(x) = q(g(x)) ==> p'(x) = q(g(x))g'(x) = h(g(x))g'(x)

g integral (x) g( integral x) integral c u(x) = h(t)dt = h(t)dt + h(t)dt c (f(x) f(x)

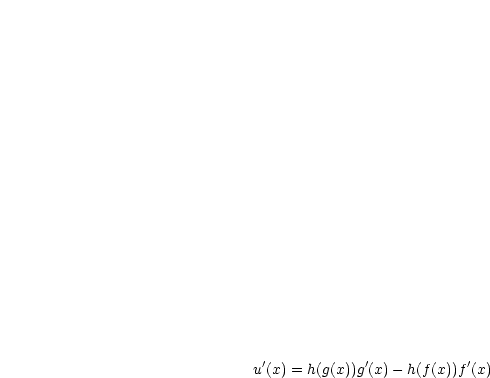
u'(x) = h(g(x))g'(x)- h(f(x))f'(x)

Übung:

sinx integral --dt--- p(x) = 1+ sint x3

9.4.3 Die partielle Integration

Satz:

$f$ , $1 g (- C [a,b]$ . Dann gilt:

$b b integral ' b integral ' f (t)g(t)dt = f(t)g(t)|a- f (t)g(t)dt a a$

Oder: $integral integral f (t)g'(t)dt = f(t)g(t) - f'(t)g(t)dt$

Beweis:

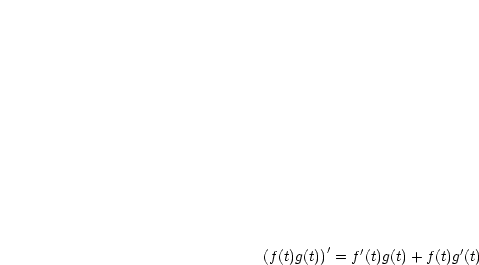
(f(t)g(t))'= f'(t)g(t)+ f(t)g'(t)

integral b integral b integral b (f (t)g(t))'dt = f(t)g(t)| ba = f'(t)g(t)dt+ f(t)g'(t)dt a a a

Beispiele:

integral dt integral 1 1 integral dt tln-t = t ln-tdt = 1 + tlnt g(t) f(t)

==> 1 = 0

' --1--1 g(t) = lnt,f (t) = - (ln t)2t

integral x x integral -dt-= 0 + -dt- c tln t c tlnt

Hier drehen wir uns im Kreis, wir wenden einen Trick an:

integral x dt integral x 1 ----= -tdt = ln (lnx) tln t lnt

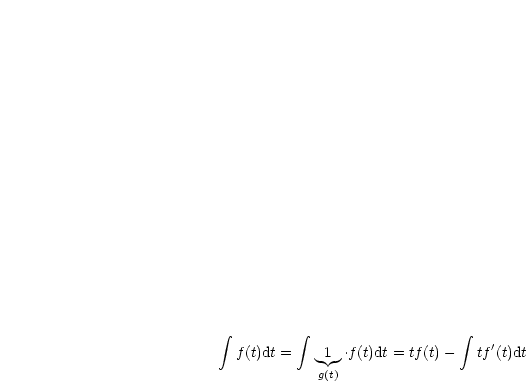
integral integral integral f (t)dt = 1 .f(t)dt = tf(t) - tf '(t)dt g(t)

integral integral ln tdt = tln t- dt = tlnt- t

integral V~ ----- V~ ------ integral V~ ------ integral 2 1- x2dx = x 1- x2- x1 V~ --2x-dx = x 1- x2 - V~ --x--dx = integral 2 1- x2 integral 1- x2 V~ ----2- 1--x2--1- V~ -----2 V~ ----2- = x 1- x - V~ 1---x2 dx = x 1 - x - 1- x dx + arcsin x

(9.5)

integral V~ ----- ( V~ ------ ) 1 - x2dx = 1 x 1- x2 + arcsin x 2

+ integral 1 V~ ------ ( V~ ------ )|1 1 -x2dx = 1 1- x2 + arcsin x || = 1 arcsin1 = p- 2 |-1 2 2 -1

Wir haben gerade die Fläche eines Halbkreises berechnet.

[next] [prev] [prev-tail] [front] [up]