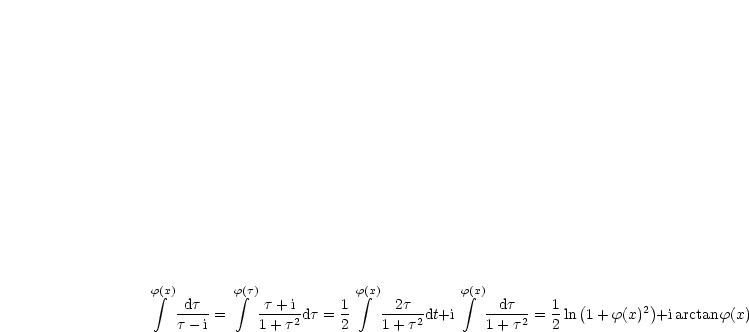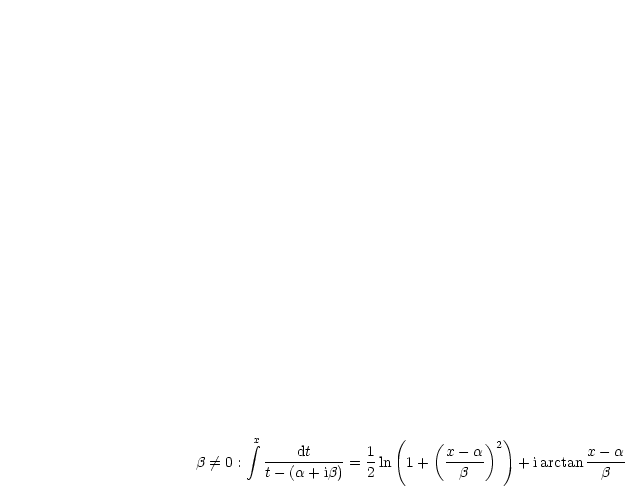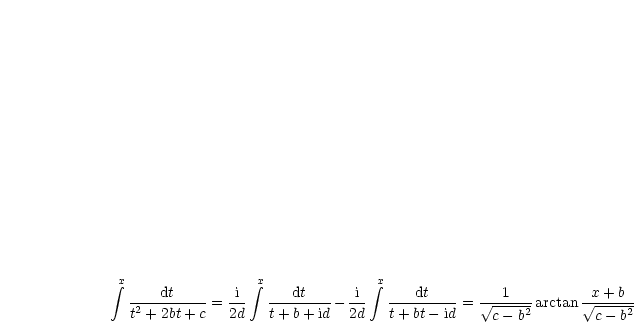9.5 Die Substitutionsregel

[next] [prev] [prev-tail] [tail] [up]

9.5 Die Substitutionsregel

Satz:

$I$ sei beschränktes Intervall, $f (- C1[a,b]$ : $f$ : $[a,b] '--> I$ , $f (- C0(I)$ . Dann gilt:

$integral b f integral (b) f (f(t))f'(t)dt = f(x)dx a f(a)$

Setze $x = f(t)$ : $dx dt-= f'(t) ==> dx = f'(t)dt$

Beweis:

integral t G(t) = f(f(t))f'(t)dt : G(a) = 0,G'(t) = f(f(t))f'(t) a

f integral (t) H(t) = f(x)dx f(a)

H(a) = 0,H'(t) = f(f(t))f'(t)

a < t < b

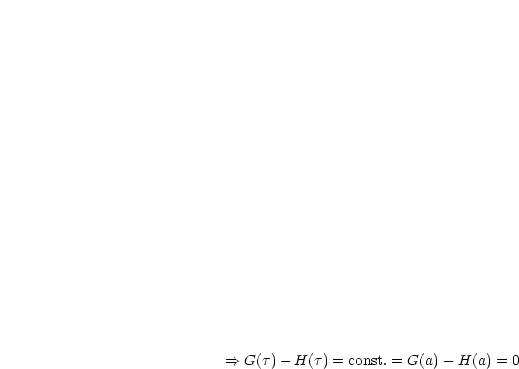
==> G(t)- H(t) = const.= G(a) -H(a) = 0

==> G(t) = H(t),a < t < b

==> G(b) = H(b)

Beispiele:

integral b b integral +c f(t) = t +c : f(t+ c)dt = f(t)dt a a+c

integral x x integral -c ||x- c ---dt--= dt= -1--t1-n|| = --1------1----,n > 1 (t- c)n tn 1- n 1 -n (x- c)n-1

f(t) = 1n-: f(t- c) t

f(t) = tc

f'(t) = c

integral b integral bc c f(tc)dt = f(t)dt a ac

Dies können wir beispielsweise bei der Berechnung des folgenden Grenzwertes verwenden:

integral b lim f(t)dt c'-->0 a

b bc integral 1 integral +f (bc)b- f(ac)a lcim'-->0 f(tc)dt = lcim'-->0 c f (t)dt = cli'-->m0-------1-------= f(0)(b -a) a ac

Übung:

Es sei $a = 0$ und $c = - 1$ :

Ist $f$ gerade, so gilt: $integral b integral b f(t) dt = 2 f(t)dt a 0$ .
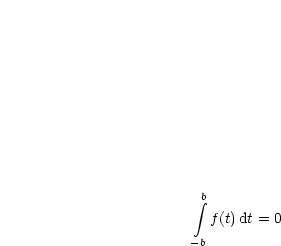Ist $f$ ungerade, so gilt: $integral b f(t)dt = 0 - b$ .

9.5.1 Integration von komplexen Funktionen

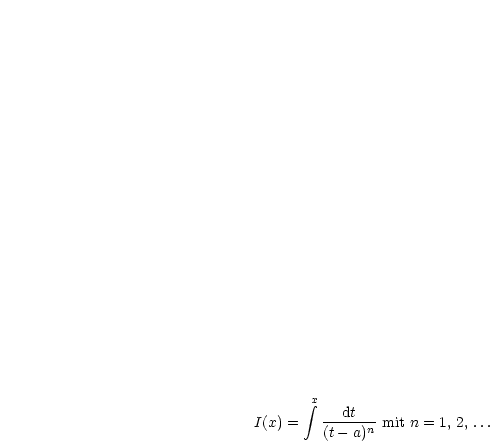
integral x I(x) = ---dt-- mit n = 1, 2, ... (t- a)n

$n > 1$ haben wir schon berechnet.

integral x I(x) = --dt-mit a (- C t- a

Da der Logarithmus einer komplexen Zahl teuflisch ist, wird dieses Problem erst später behandelt.

$a (- R$ : $integral x -dt-= ln|x- a| t- a$
$a (- C$ : $a = x+ ib(b /= 0)$

$x integral integral x integral x ----dt----= ---1---1dt = f(f(t))f'(t)dt mit f(t) =-1--,f(t) = t--a t- (a+ ib t-ba - ib t- i b$

$f integral (x) f integral (t) f integral (x) f integral (x) -dt- = -t-+i-dt = 1 -2t--dt+i -dt---= 1 ln(1 + f(x)2)+iarctanf(x) t - i 1 + t2 2 1+ t2 1+ t2 2$

$integral x ( ( ) ) ----dt---- 1 x--a- 2 x---a b /= 0 : t- (a + ib) = 2 ln 1+ b + iarctan b$

Anwendung:

x integral ----dt---- J = t2 + 2bt+ c f¨ur b,c (- R

V~ ----- t2 + 2bt+ c = (t+ b)2 + c- b2 = 0,c- b2 > 0,d = c - b2

2 t + 2bt+ c = (t+ b+ id)(t+ b - id)

----1----- ----A--- ---B---- -i i- t2 + 2dt+ c = t +b + id + t+ b- id Bestimme: A = 2i,B = - 2d

integral x dt i integral x dt i integral x dt 1 x+ b t2 +-2bt+-c = 2d t+-b+-id-- 2d t+-bt--id-= V~ c---b2 arctan V~ c---b2

Beispiel:

p2 integral --cost--- 1+ sin2tdtx = sint 0

dx = cos dt

sin p-= 1,sin0 = 0 2

integral p2 integral 1 --cost--dt = -dx---= arctan1 = p- 1 + sin2t 1+ x2 4 0 0

[next] [prev] [prev-tail] [front] [up]