|
Jedes Polynom vom Grad |
|
|
Jedes Polynom vom Grad |
|
 | (9.6) |
 eine Nullstelle des Polynoms
eine Nullstelle des Polynoms  . Dann gilt:
. Dann gilt:

Wir erinnern uns:
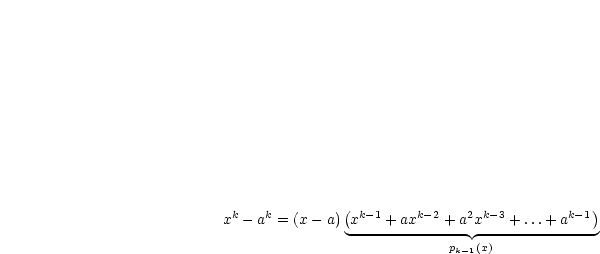
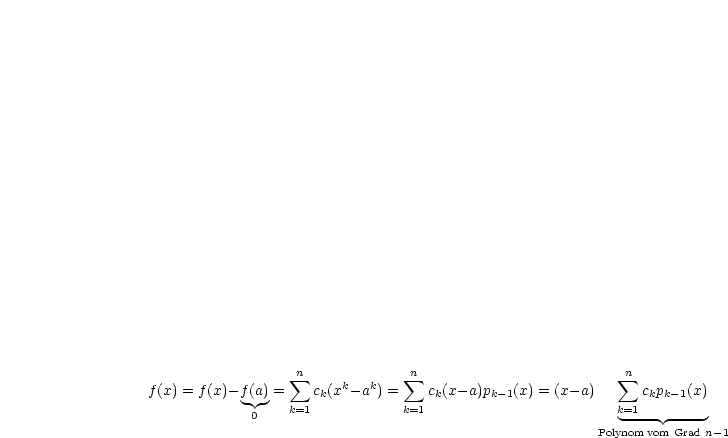
|
Ein Polynom |
|

Unter den Nullstellen  ,
,  ,
,  sind
sind 
 verschiedene
verschiedene  ,
,  ,
,
 ,
,  .
.

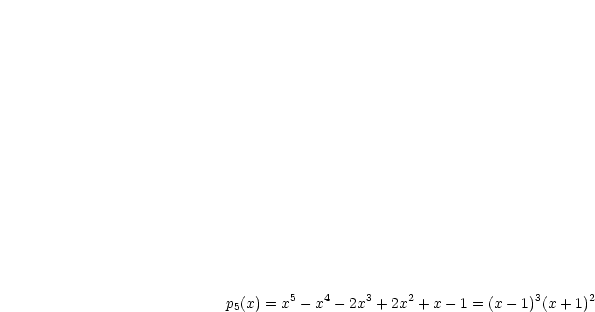



 sei rationale Funktion grad
sei rationale Funktion grad . Es sei
. Es sei
 ,
,  . Dann gilt:
. Dann gilt:
Es gibt eindeutig eine Zahl  und ein Polynom
und ein Polynom  mit grad
mit grad und
und
 .
.

Für  gilt:
gilt:
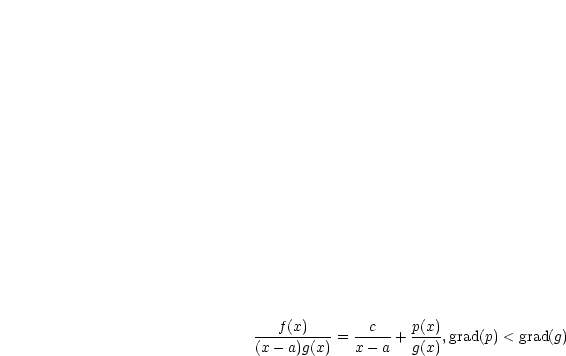
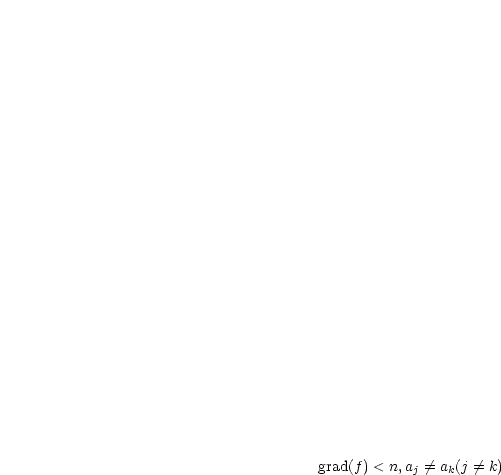
 | (9.7) |

A3  ,
,  ,
,  ,
,  ,
,  seien wie oben. Dann gibt es eindeutig Zahlen
seien wie oben. Dann gibt es eindeutig Zahlen
 ,
,  ,
,  und ein Polynom
und ein Polynom  mit grad
mit grad , so daß
gilt:
, so daß
gilt:

|
|
|
|
|

Durch Polynomdivision ein Polynom abspalten.

Wende Satz auf  an.
an.
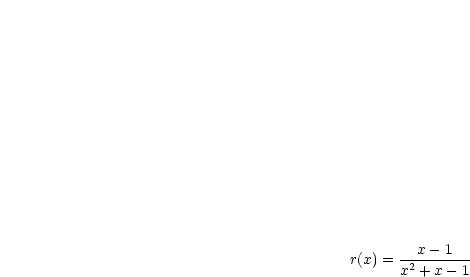
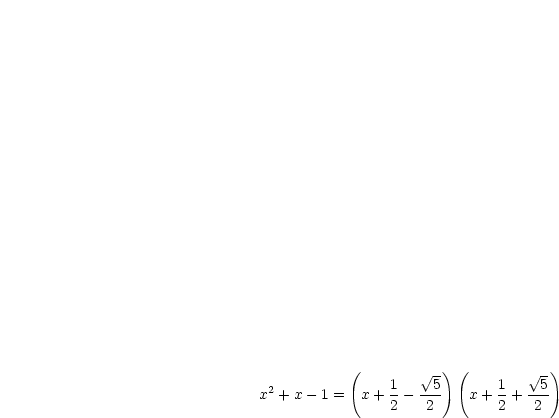
Damit folgt für  :
:


Partialbruchzerlegung berechnen zu  ,
,  :
:



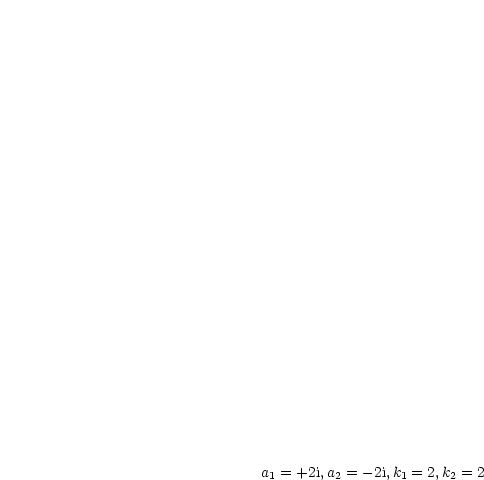





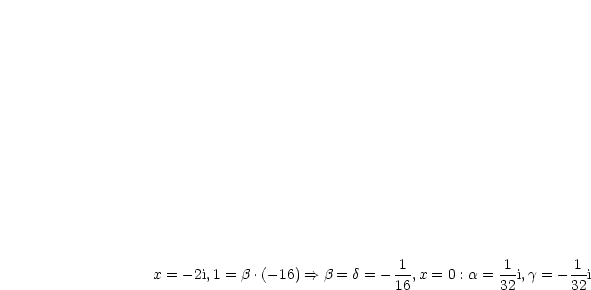
Damit ergibt sich für  :
:
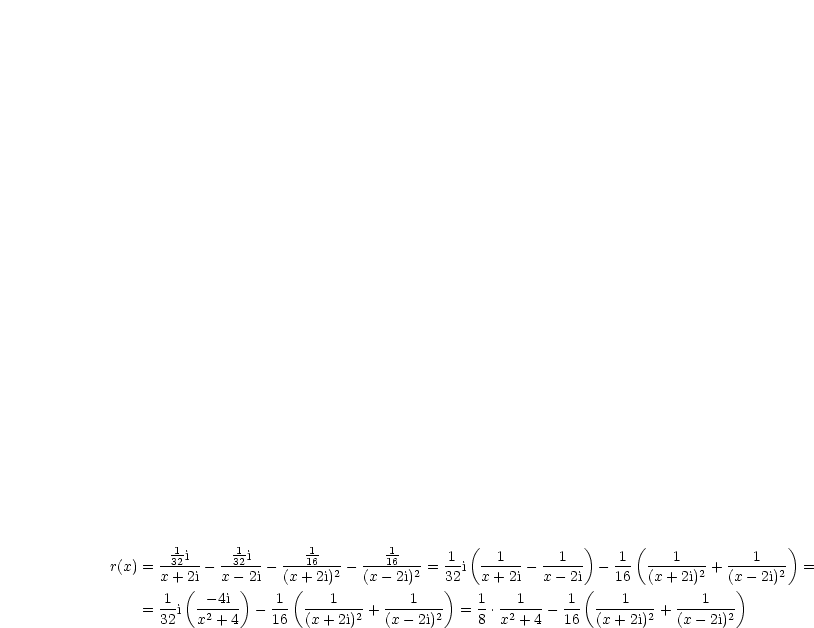 | (9.8) |
Damit ergibt sich nun für das Integral:
 | (9.9) |
Gegeben sei folgende vom Parameter  abhängige Funktion:
abhängige Funktion:

Es sollen alle  bestimmt werden, für welche die Stammfunktion von
bestimmt werden, für welche die Stammfunktion von  eine
rationale Funktion ist. Außerdem soll dann die Stammfunktion zu diesen
eine
rationale Funktion ist. Außerdem soll dann die Stammfunktion zu diesen  berechnet werden.
berechnet werden.
Dazu führen wir folgende Partialbruchzerlegung durch:
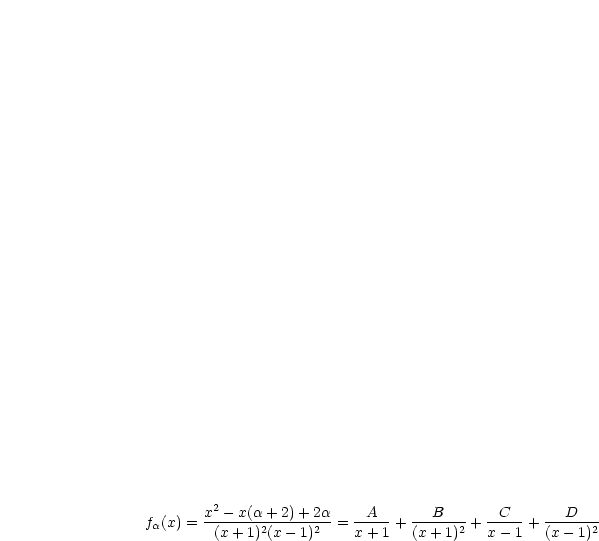
Die Parameter  und
und  können mittels der Zuhaltemethode bestimmt
werden:
können mittels der Zuhaltemethode bestimmt
werden:


Wir bringen die beiden bestimmten Terme auf die linke Seite:

Wir können den Zähler durch die Faktoren  und
und  des Nenners durch
Polynomdivision kürzen:
des Nenners durch
Polynomdivision kürzen:

Damit folgt nun  und
und  wieder mit der Zuhaltemethode:
wieder mit der Zuhaltemethode:
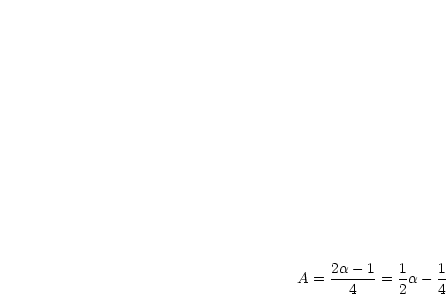

Damit haben wir also die Funktion  in Linearfaktoren zerlegt:
in Linearfaktoren zerlegt:

Die Stammfunktion von  ist rational, wenn die Terme proportional zu
ist rational, wenn die Terme proportional zu  wegfallen. Dies ist für folgende
wegfallen. Dies ist für folgende  der Fall:
der Fall:


Somit gibt es nur ein  , welches die Bedingung erfüllt. Die zugehörige
Stammfunktion lautet:
, welches die Bedingung erfüllt. Die zugehörige
Stammfunktion lautet:

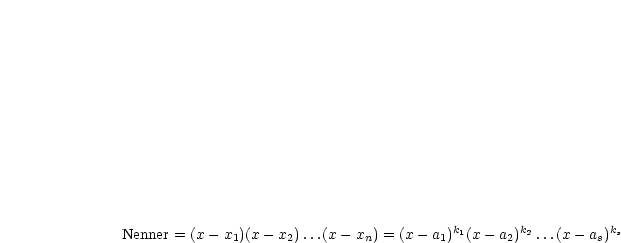




Substituiere  (Rekursionsformel)
(Rekursionsformel)