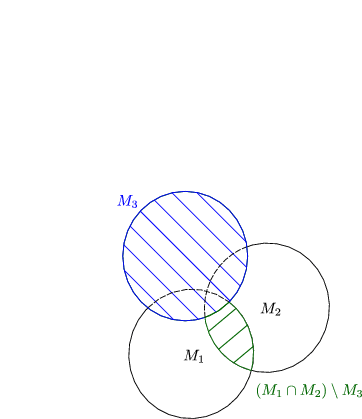
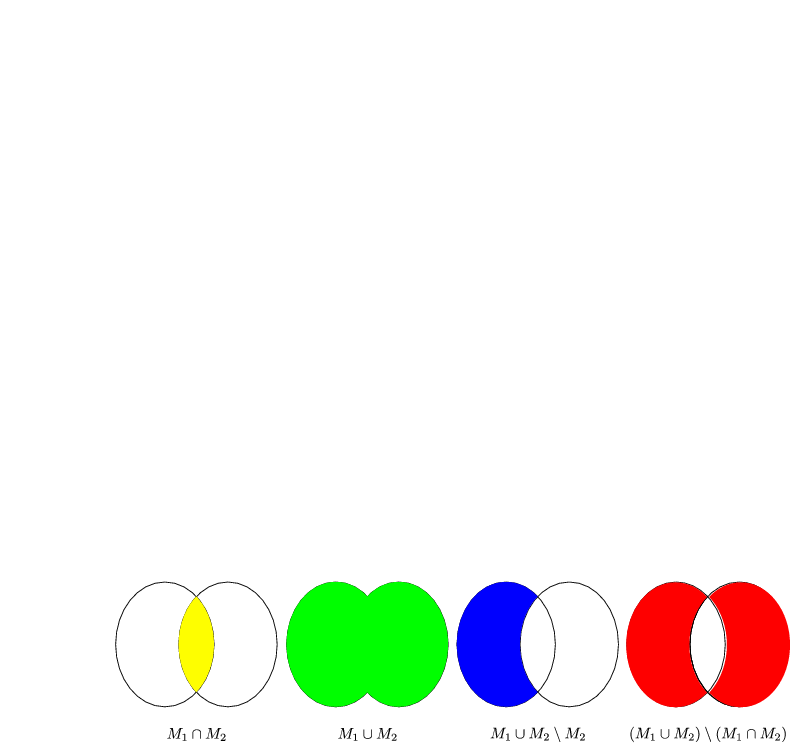, ,  , ,  , ,  seien Mengen. Ist seien Mengen. Ist  eine Teilmenge von eine Teilmenge von  , so folgt aus , so folgt aus  stets stets  . . |
    : :  |
 , ,  , ,  , ,  seien Mengen. Ist seien Mengen. Ist  eine Teilmenge von eine Teilmenge von  , so folgt aus , so folgt aus  stets stets  . . |
    : :  |

Mittels dieser Definition kann man dann für die eingeführten Zahlenmengen schreiben:

 |
 |
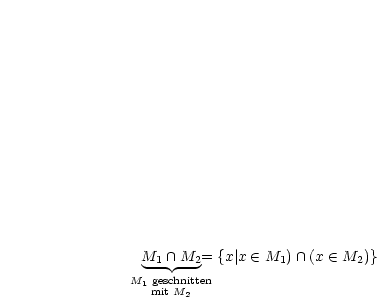 |



 ,
, 

 bedeutet
bedeutet  .
.
 , ,  , falls , falls  weder in weder in  noch in noch in  liegt. liegt. |
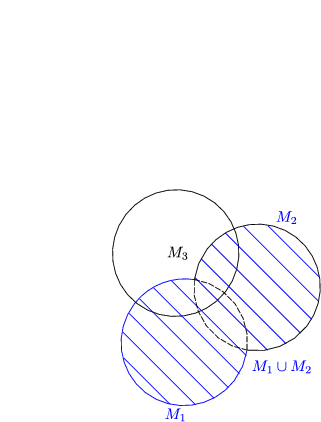





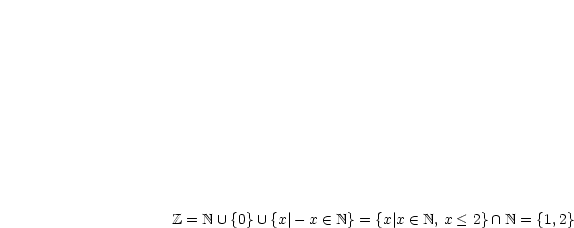
 ist die Menge, die kein Element enthält: die leere Menge. ist die Menge, die kein Element enthält: die leere Menge. |