2.7 Eigenwertprobleme/Diagonalisierung von Matrizen

Wir schauen uns die Bewegungsgleichungen zweier Pendel der Masse $m$ und Länge $l$ an. Diese folgen aus den Newtonschen Gesetzen:

mlf¨ = - mgf + k(f - f ) 1 1 2 1

mlf¨2 = - mgf2 - k(f2- f1)

$f1 = f1(t)$ und $f2 = f2(t)$ sind gesucht. Dies ist ein gekoppeltes System von Differentialgleichungen. Es handelt sich um gekoppelte Pendel. Setze nun $x1 = mlf1$ , $x2 = mlf2$ , $a = gl$ und $b = mkl$ . Damit erhalten wir dann folgendes Differentialgleichungssystem:

x¨1 = -ax1 + b(x2- x1)

x¨2 = -ax2 - b(x2- x1)

( ) x = x1 x2

( -a + b b ) A = +b -a - b

¨x(t) = Ax(t)

Wir wollen dies entkoppeln mit einer konstanten regulären (2,2)-Matrix $C$ wie folgt:

y(t) = C-1x(t),x(t) = Cy(t)

( ) Cy(t) = ACy(t) ==> ¨y(t) = C- 1ACy(t) = c1 0 0 c2

y¨1(t) = c1y1(t)

y¨2(t) = c2y2(t)

Definition:

$A (- (m,n)$ heißt diagonalisierbar, falls es eine reguläre Matrix $C$ so gibt, daß $C -1AC$ Diagonalgestalt hat.

$( c1 0 ... 0 ) 0 c2 ... 0 C-1AC = D = diag(c1,c2,...,cn) = .. .. .. .. . . . . 0 0 ... cn$

Angenommen, $A$ ist diagonalisierbar: $c1$ , $c2$ , $...$ , $cn$ seien die Spalten von $C$ .

AC = CD = [Cc1e1,Cc2e2,...,Ccnen] = [c1c1,c2c2,...,cncn]

AC = [Ac1,Ac2,...,Acn]

Ack = ck

Ack = ckck f¨ur k = 1,2,...,n

Eigenwertproblem (EWP):

Suche Vektoren $v (- Cn$ , $v /= o$ , und Zahlen $c (- C$ mit $Av = cv$ $(*)$ .

Definition:

Jede Lösung $v /= o$ von $(*)$ heißt Eigenvektor (EV) von $A$ zum Eigenwert $c$ .

Satz:

$A (- C(m,n)$ ist diagonalisierbar. $<==>$ $A$ besitzt $n$ linear unabhängige Eigenvektoren.

Beweis:

„ $==>$ “:
Die Spalten von $C$ sind $n$ linear unabhängige Eigenvektoren und die Diagonalelemente sind die zugehörigen Eigenwerte.
„ $<==$ “:
$c1$ , $...$ , $cn$ seinen die linear unabhängigen Eigenvektoren mit den Eigenwerten $c1$ , $...$ , $cn$ : $Ack = ckck$ für $k = 1$ , 2, $...$ , $n$

Definition:

Es sei $C = [c1,...,cn]$ und $- 1 Cek = ck,ek = C ck$ .

$( ) c1 0 ... 0 C-1(AC) = C-1[Ac ,Ac ,...,Ac ] = C-1[c c ,c c,...,c c ] = 0 c2 ... 0 1 2 n 1 1 2 2 n n ... ... ... ... 0 0 ... cn$

Bestimmen von Eigenwerten und Eigenvektoren:

Gegeben ist $(m,n) A (- C$ . Gesucht sind $c (- C$ derart, daß das lineare Gleichungssystem $(A - cE)x = o$ nichttriviale Lösungen hat.

Satz:

$c$ ist Eigenwert von $A$ . $<==>$ $rang(A - cE) < n$ $<==>$ $det(A -cE) = 0$

Dies ist die sogenannte charakteristische Gleichung. $c$ ist Nullstelle des charakteristischen Polynoms. $0 = det(A - cE)$

( ) a11- c a12 a13 ... a1n a21 a22- c a23 ... a2n det(A - cE) = det ... ... ... ... ... = a ... ... a a - c nn nn-1 nn n-2 = (a11- c)(a22- c)...(ann - c+ {vom Grad < c }= n n n-1 n-1 sum n 0 = (-1) c + (- 1) c ajj+ ...+ c det(A) j=1 -- Spur (A)

(2.10)

Satz:

$n sum k xA(c) = det(A - cE) = ckc k=0$ mit $n cn = (-1)$ , $n-1 cn- 1 = (-1) Spur(A)$ , $c0 = det(A)$

Beispiel:

( ) 0 1 0 0 0 0 0 1 0 0 A = 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0

5 det(A - cE) = (-c) = 0

$c = 0$ ist einziger Eigenwert der Vielfachheit $n = 5$ .

rang(A - 0E) = 4

Damit ergibt sich also:

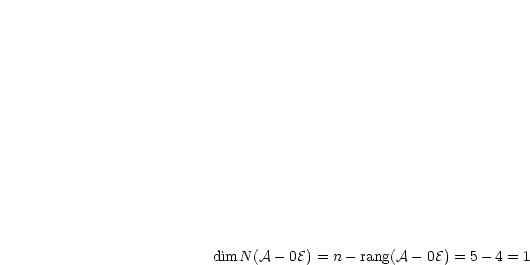
dimN (A - 0E) = n- rang(A -0E) = 5- 4 = 1

Das heißt, es gibt einen linear unabhängigen Eigenvektor. Die Matrix ist somit nicht diagonalisierbar, weil wir zur Diagonalisierung nämlich 5 Eigenvektoren benötigten.

Beispiel:

Betrachten wir folgende Matrix:

( ) 3 2 - 1 A = 2 6 - 2 0 0 2

Zuerst berechnen wir die Eigenwerte:

det(A - cE = -(c - 2)2(c- 7) = 0

Diese Gleichung hat die einfache Lösung $c1 = 2$ und die zweifache Lösung $c2 = 7$ . Hierzu bestimmen wir die Eigenvektoren:

Eigenvektor zu $c1 = 2$ : $(1 2 -1) (v1 ) (0 ) 2 4 -2 v2 = 0 0 0 0 v3 0$

$|--------------| n = 3 : rang(A -2E) = 1 ----------------$
Somit gibt es 2 linear unabhängige Eigenvektoren zu $c1 = 2$ :
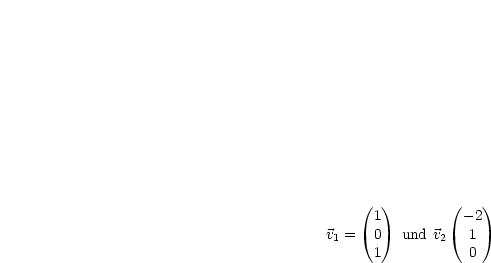
$( ) ( ) 1 -2 v1 = 0 und v2 1 1 0$
Eigenvektor zu $c2 = 7$ : $( -4 2 - 1) (v1) (0 ) 2 - 1 - 2 v2 = 0 0 0 - 5 v3 0$

$|--------------| n = 3 : rang(A--7E)-=-2$
Somit gibt es einen linear unabhängigen Eigenvektor zu $c = 7 2$ :
$( ) 1 v3 = 2 0$

Wir haben nun 3 linear unabhängige Eigenvektoren. Folglich ist die Matrix $A$ diagonalisierbar.

Beispiel:

(cos f - sinf ) A = sin f cosf

Eine reelle Matrix kann komplexe Eigenwerte haben.

|--------------------| |c1 = eif und c2 = e-if ---------------------

Auch können dann die Eigenvektoren komplex sein:

|---(--)---------(--)-| v1 = i und v2 = 1 | ------1------------i---

( ) A ist Diagonalisierbar zum Beispiel mit C = i 1 1 i

<(i ) (i )> ( 1 ) 1 , 1 = (i,1) -i = 0 : v1 _L v2

( ) ( ) -1- i 1 * -T -1 -1- -i 1 C = V~ 2 1 i ist unit¨ar: C = C = C = V~ 2 1 - i

|-------(--------)-| | * eif 0 | |C AC = 0 e- if | --------------------

Vorbemerkungen:

$B(A - cE) = {x|x$ ist Eigenvektor von $A$ zu $c}$ $U$ ${o}$ ist komplexer Vektorraum. Er hat die Dimension $n - rang(A - cE) = dim = dimE(c)$ (geometrische Vielfachheit von $c$ ). $----------- det(A - cE)XA(c) = 0$ hat genau $n$ Lösungen.

~c1,~c2,...,~cn = (- 1)n(c- ~c1)(c- ~c2)...(c- ~cn) = (-1)n(c-c1)m1(c- c2)m2 ...(c- ck)mk

Hiervon sind $c1$ , $...$ , $ck$ $(1 < k < n)$ verschieden mit den Vielfachheiten. $m1$ , $m2$ , $...$ , $mk$ sind die algebraischen Vielfachheiten, womit gilt:

k sum m = n j=1 j

Daraus ergibt sich also:

$cn-1$ : $n k n( ~ ~ ~ ~ ) n-1 sum ~ n-1 sum (-1) - cn- cn- 1- cn-2- ...- c1 = (- 1) cj = (-1) mjcj j=1 j=1$
$0 c$ : $((- 1)n(-1)n~c ~c ...~c )= cm1cm2 ...cmk 1 2 n 1 2 k$

Satz:

$A (- C(m,n)$ habe die $k$ $(1 < k < n)$ verschiedenen Eigenwerte $c1$ , $...$ , $ck$ mit den algebraischen Vielfachheiten $m1$ , $m2$ , $...$ , $mk$ $( ) sum k mj = n j=1$ . Dann gelten:

$prod k XA(c) = det(A - cE) = (-1)n (c- cj)mj j=1$

Man hat außerdem:

$prod k det(A) = cmjj j=1$
$sum k Spur(A) = mjcj j=1$

Es gilt $1 < dimE(cj) < mj$ $(mj$ ist algebraische Vielfachheit von $cj$ .)

Folgerung:

$A$ ist singulär. $<==>$ $A$ besitzt den Eigenwert 0.
$A$ ist regulär. $<==>$ Alle Eigenwerte sind von Null verschieden.

Satz:

Hat $A$ die verschiedenen Eigenwerte $c1,...,ck$ mit den Eigenvektoren $v1,v2,...,vk.$ Dann sind $v1,...,vk$ linear unabhängig.

\text{[math]}

Unser Ziel ist:

Aus 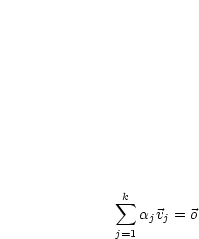$sum k ajvj = o j=1$ muß auf $a1 = ...= ak = 0$ geschlossen werden. Wir führen eine vollständige Induktion durch:

Induktionsanfang $k = 1$ : $a1v1 = o ==> a1 = 0$
Dies ist trivial!
Induktionsschluß $k- 1 '--> k$ : $k k sum a c v = sum a Av = o j=1 j j j j=1 j j } k sum +1 sum k ==> aj(cj- ck)vj = o ajckvj = o j=1 j=1$

$aj(cj - ck) = 0 f¨ur j = 1,2,...,k- 1$
Mit der Induktionsvoraussetzung ergibt sich dann:
$a1 = ...= ak-1 = 0 ==> ak = 0$

Folgerung:

Hat die Matrix $A$ $n$ verschiedene Eigenwerte, so ist sie diagonalisierbar.

Satz:

Die Matrix $(m,n) A (- C$ hat genau dann linear unabhängige Eigenvektoren, wenn für jeden Eigenwerte die algebraische Vielfachheit und geometrische Vielfachheit übereinstimmen.

Satz:

Es sei $(m,n) A (- C$ hermitesch $* (A = A )$ . Dann gelten:

Alle Eigenwerte sind reell.
Eigenvektoren zu verschiedenen Eigenwerten sind orthogonal zueinander.
$A$ hat $n$ orthogonale Eigenvektoren, das heißt, $A$ läßt sich in einer unitären Matrix diagonalisieren.

Satz:

$A (- R(m,n)$ sei symmetrisch ( $A = AT$ ). Dann gibt es ein Orthonormalsystem $x1,x2,...,xn$ von Eigenvektoren, das heißt: $C-1AC = CTAC = diag(c1,...,cn) mit C = [x1,...,xn]$ .

Auswertung zu vorhergehendem Satz:

Diagonalisiere die symmetrische Matrix $A$ : $c1,c2,c3,...,cp$ seien verschiedene Eigenwerte.


$c1$	$c2$	$c3$	$...$	$cp$

( $m1$ )	( $m2$ )	( $m3$ )	$...$	( $mp$ )

dim $E(c1)$	dim $E(c2)$	dim $E(c3)$	$...$	dim $E(cp)$


Basis:

$v(1) 1$ , $...$ , $v(1m)1$	$v(2) 1$ , $...$ , $v(m22)$	$v(3) 1$ , $...$ , $v(m33)$	$...$	$v(p) 1$ , $...$ , $v(pm)p$



SCHMIDTsches Orthonormalisierungsverfahren:
$y(1) 1$ , $...$ , $y(1) m1$	$y(2) 1$ , $...$ , $y(2) m2$	$y(3) 1$ , $...$ , $y(3) m3$	$...$	$y(p) 1$ , $...$ , $y(p) mp$



Umbenennung:

$x 1$	$x 2$	$x 3$	$...$	$x p$

Vorbereitung zu nächstem Satz:

<u,v> = utv

<Ax, y> = (Ax)Ty-= xTATy-= xTA*y-= xTA*y-= <x,A*y >

Ist $A$ hermitesch, so gilt $<Ax,y> = <x$ , $Ay>$ $A$ $x$ , $y (- C$ .

Satz 7, 1.):

<Ax,y> = <x,Ay > A x,y

Sei $c$ Eigenwert, $x 0$ sei Eigenvektor, also gelte $Ax = cx 0 0$ . Setze $x = y = x 0$ :

<cx ,x > = <x ,cx > 0 0 0 0

c ||x|| 2 = c||x ||2 ==> c = c, das heißt c (- R 0 0

Satz 7, 2.):

Für $c1 /= c2$ gilt:

Ax1 = c1x1,Ax2 = c2x2

Unser Ziel ist $<x1,x2> = 0$ :

<c1x1,x2> = <x1,c2x2> ==> c1<x1,x2 = c2<x1,x2> ==> (c1--c2)<x1,x2> = 0 /=0

2.7.1 Definitheit reeller Matrizen

Es sei $(m,n) A (- R$ und $T A = A$ . Ordne $A$ die Funktionen $Q$ : $n R '--> R$ mit $T Q(x) = x Ax$ zu. Im Falle $n = 3$ gilt:

( ) q1 2 2 2 A = (ajk),x = q2 : Q(q1,x2,x3) = a11q1+a22q2+a33q3+(a12 + a21)q1q2+(a13-+ a31)q1q3+(a23-+-a32)q2q3 q3 2a12 2a13 2a23

Definition:

$A$ heißt positiv definit $<==>$ $xTAx > 0$ $A$ $x /= o$
$A$ heißt positiv semidefinit $<==>$ $T x Ax > 0$ $A$ $x$
$A$ heißt indefinit $<==>$ Es gibt $x1,x2$ mit $xTAx1 > 0,xTAx2 < 0 1 2$
$A$ heißt negativ (semi)definit $<==> -A$ ist positiv (semi)definit.

Satz:

$(m,n) A (- R$ , $T A = A$ . Dann gelten:

$A$ positiv definit $<==>$ Alle Eigenwerte sind $> 0$ .
$A$ positiv semidefinit $<==>$ Eigenwerte sind $> 0$ , mindestens einer ist $= 0$ .
$A$ indefinit $<==>$ Es gibt Eigenwerte $c1$ , $c2$ mit $c1 > 0$ , $c2 < 0$

Nachrechnen:

$A$ besitzt ein Orthonormalsystem von Eigenvektoren $T v1,...,vn: Avj = cjvj,vjvk = djk Basis in Rn$ .

( )T ( )T sum n sum n ( sum n ) sum n ( sum n ) x = qjvj : Q(x) = xTAx = qjvj A qkvk = qjvj qkckvk = j=1 j=1 k=1 j=1 k=1 sum n sum n sum n = qjqkckvTjvk= q2jcj j k d | j=1 jk

(2.11)

Positive Definitheit:
Ist $A$ positiv definit, also $Q(x) > 0$ $A$ $x /= o$ , dann gilt $Q(vk) = ck > 0$ . Also sind alle Eigenwerte $> 0$ . Sind umgekehrt alle Eigenwerte $> 0$ , so gilt:
$sum n Q(x) = q2jcj > 0 A x /= o j=1$
Dann ist $A$ positiv definit.
Indefinitheit:
$A$ ist indefinit, wenn $Q(x1) > 0,Q(x2) < 0$ . Es gibt einen positiven und einen negativen Eigenwert (mit Widerspruch zu vorher).
$Q < Q(v1) = c1,Q(v2) = c2 < 0 <== c1 > 0,c2 < 0$

Im Falle $n = 2$ kann man dies folgendermaßen feststellen:

( ) A = a b (- R(2,2) ist b c

Positiv definit $<==>$ $a > 0$ und $ac- b2 > 0$
Negativ definit $<==>$ $a < 0$ und $ac- b2 > 0$
Positiv semidefinit $<==>$ $a + c > 0$ und $ac- b2 = 0$
Indefinit $<==>$ $ac- b2 < 0$

Beweis (als Übung):

$c1,c2$ sind die Eigenwerte von $A$ :

a +c = c1 + c2

ac- b2 = c1 .c2

Es ist $R(m,n) - ) A = (ajk)j,k=1,...,n$ und $A = AT$ .

( ) a11 a12 ... a1k D det a21 a22 ... a2k wobei k = 1, 2, ..., n k ... ... ... ... ak1 ... ... akk

Satz:

$A$ sei positiv definit. $<==>$ $D1 > 0$ , $D2 > 0$ , $...$ , $Dn > 0$ ( $=$ Satz 2 für $n = 2)$

2.7.2 Quadriken (Kegelschnitte, Flächen 2.Grades)/Hauptachsentransformation

In der Schule:

Gerade (im $R2$ ): $ax + by+ c = 0$
Ebene (im $3 R$ ): $ax+ by+ cz + d = 0$

Jetzt in der Universität:

Kegelschnitt (im $R2$ ): $ax2 + bxy+ cy2 + dx + ey+ f = 0$
Flächen (im $R3$ ): $ax2 + by2 + cz2 + dxy + exz + fyz + gx + hy+ jz + k = 0$

Zylinder, Kugel, Ellipsoide usw. können so dargestellt werden. Diese Formen kann man folgendermaßen schreiben:

( d e) ( ) ( ) ( ) ad 2 2f x ( ) x x y z 2e bf 2 y + g h j y + k = 0 2 2 c z z

Definition:

Es sei $(m,n) A (- R$ , $h$ : $n R '--> R$ mit $T T h(x) = x Ax + 2bx + c$ und $n b (- R$ mit $c (- R$ . Die Menge $n {x (- R | h(x) = 0}$ heißt Quadrik, im Fall $n = 2$ Kegelschnitt und im Fall $n = 3$ Fläche 2.Grades.

Beispiel:

Wir betrachten $q12+ q22- q23 = 0$ .

Schnitt mit $(q2,q3)$ -Ebene: $q1 = 0$ $==>$ $q22 -q23 = 0$ $==>$ 1. und 2.Winkelhablierenden in Ebene
Schnitt parallel zur $(q ,q ) 1 2$ -Ebene: $q = c 3$ $==>$ Kreise

Bei dieser Figur handelt es sich somit um einen Doppelkegel.

Satz:

Normalformen für $h(x)$ : Es sei $A (- R(m,n)$ symmetrisch.

$T T h(x) = x Ax + 2b x +c$ läßt sich durch die Transformation $T x '--> y = V (x- p)$ , $|----------| -x-=-Vy+-p-|$ mit einer orthogonalen Matrix $V$ $(detV = +1)$ und einem Vektor $n p (- R$ überführen in einen der folgenden Normalformen:

$sum r 2 cjjj + b = h(Vy + p) j=1$ , $r = rang(A)$
$sum r cjj2j + 2gjn = h(Vy+ p) j=1$ , $rang(A) < n$ mit $p > 0$

$x '--> y$ heißt Hauptachsentransformation.

Einige Bemerkungen zur Hauptachsentransformation:

$v1$ , $...$ , $vn$ sei Orthonormalsystem von Eigenvektoren von $A$ : $V = [v1$ , $...$ , $vn]$ . $y = o$ $==>$ $x = p$ wird der neue Koordinatenursprung.

V ej = vj ==> x = vj + p

Durch $x = V y+ p$ wird der Übergang vom Koordinatensystem $o$ , $e1$ , $...$ , $en$ zum System $p$ , $v1$ , $...$ , $vn$ beschrieben. $x$ hat in dem neuen System die Darstellung $n x = p+ sum j v j=1 j j$ . Die $j ,j ,...,j 1 2 n$ -Achsen sind die Hauptachsen der Quadrik.

Vy '--> Vx Drehung + Translation -------- -------- Bewegung

1.Schritt:

^ T T h(y) = h(Vy + p) = (Vy+ p) A (Vy + p)+ 2b (Vy + p)+ c = (yTVT + pT)(AVy + Ap) + 2bT (Vy + p)+ c = T T T T T T T = y V AVy + p AVy +y V Ap +p Ap + 2b (Vy + p)+ c

(2.12)

Außerdem gilt:

yTVTAp = (yTVTAp)T = pTATVy = pTAVy

Damit können wir also schreiben:

( ) ^h(y) = yTVTAVy+2pTAVy+pTAp+2bT (Vy + p)+c = yTVTAVy+2 pTA + bT Vy+pTAp+2bTp+c

Wir schreiben $V = [v1,...,vn]$ , wobei ${v1,...,vn}$ ein Orthonormalsystem von Eigenvektoren $c1$ , $...$ , $cn$ sei. Es gibt $r yTVTAVy = sum cjj2 j=1 j$ verschiedene Fälle, je nachdem ob $A$ regulär oder singulär ist. Gilt rang $(A) = n - k$ für $k (- N$ , dann sind $k$ Eigenvektoren Null.

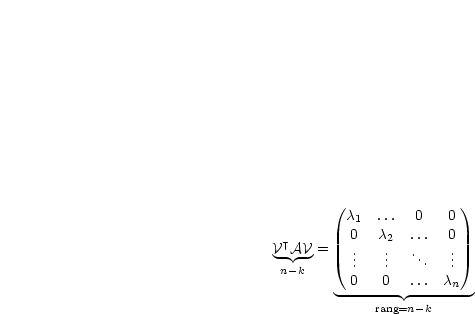
( ) c1 ... 0 0 T 0 c2 ... 0 V-AV = .. .. .. .. n-k . . . . -0---0--...-cn-- rang=n-k

Beispiel:

Wir behandeln den Fall $n = 2$ :

2 2 h(x) = - 17q1 + 18q1q2 + 7q2 + 16q1- 32q2 + 28 = 0

Wir lesen direkt ab:

( ) ( ) A = 17 9 , b = 8 , c = 28 9 7 -16

Jetzt können wir die Eigenwerte von $A$ berechnen:

( -17 - c 9 ) det 9 7- c = 0

Damit folgt dann:

(- 17- c)(7- c)- 81 = -119+ 17c - 7c+ c2- 81 = c2 + 10c -200 != 0

- 10± V~ (10)2---4.1.(-200) - 10± 30 c1/2 =------------------------- = --------= - 5± 15 2.1 2

|----------------| |c1 = 10,c2 = -20 | -----------------

Die Matrix ist regulär. Es existiert somit ein Mittelpunkt der Fläche. Für die Eigenvektoren zu $c1$ und $c2$ ergibt sich:

Zu $c1 = 10$ : $-27v + 9v = 0 11 12$
Daraus ergibt sich:
$|--------(-)-| v = V~ 1- 1 | -1----10--3---$
Zu $c2 = 20$ : $|--------(---)-| v2 = V~ 1- - 3 | -------10--1----$

Damit erhalten wir als Drehmatrix:

|----------------| | 1 (1 -3) | |V = V~ -- 3 1 | ------10----------

Außerdem gilt:

( 8 ) 1 ( -7 9)( 8 ) (1 ) p = A-1 -16 = - 200 9 17 - 16 = 1

|----------| |h(1,1) = 20| ------------

Damit resultiert schließlich für die Normalform der Quadrik:

|-------------2-----2--------| -^h(j1,j2)-=-10j1---20j2 +-20 =-0

|--------------| |2 ( j1)2 | j2 - V~ 2 = 1| ----------------

Es handelt sich um eine Hyperbel. Wir haben also folgende Transformation verwendet:

x = Vy+ p

1 3 q1 = V~ -j1- V~ -j2 + 1 10 10

--3- -1-- q2 = V~ 10-j1 + V~ 10j2 + 1

( ) ( ) ( ) j1 = 1 q1 -1-- 1 j2 = 0 ==> q2 = V~ 10 3

( ) ( ) ( ) j1 = 0 q1 1-- - 3 j2 = 1 ==> q2 = V~ 3 1

Beispiel:

Wir betrachten folgende Quadrik:

- - q21- 2 V~ 3q1q2 + 3q22 + 8 V~ 3q1- 8q2- 4 = 0

Auch hier können wir $A$ , $b$ und $c$ direkt ablesen:

( V~ -) ( V~ -) 1 V~ - - 3 4 3 A = - 3 3 , b = -4 , c = -4

Wir berechnen nun die Eigenwerte der Matrix $A$ :

( V~ - ) det c V~ --1 3 = (c- 1)(c- 3)- V~ 3. V~ 3-= c2- 4c+3- 3 = c2- 4c = c (c- 4)=!0 3 c - 3

|c-=-4, c-=-0| --1-----2-----

Hieraus ergibt sich dann folgende Drehmatrix:

|-----(------ V~ -)-| V = 1 1 V~ - 3 | ----2-----3---1----

Mit der Transformation $x '--> y$ , also $x '--> z$ und anschließend $z '--> y$ bringen wir die Quadrik auf Normalform. Zuerst führen wir also neue Koordinaten ein über:

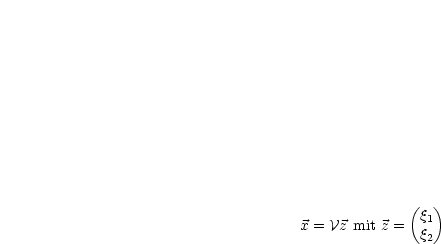
( ) q1 x = Vz mit z = q2

Die Matrix $A$ ist singulär, kann somit nicht invertiert werden. Dann ergibt sich durch Einsetzen der neuen Koordinaten und mittels anschließender quadratischen Ergänzung:

V~ - ( V~ -)2 h(Vz) = 4q21 +2bTVz - 4 = 4q21 + 8 3q1 + 8q2- 4 = 4 q1 + 3 + 8(q2 - 2)

j = q + V~ 3 1 1

j2 = q2- 2

Nun führen wir noch eine Verschiebung des Koordinatensystems durch:

( V~ -) (V ~ -) y = z + 3 = VTx+ 3 = 4j21 + 8j2 = 0 - 2 -2

Damit ergibt sich also schlußendlich folgende Normalform:

|----------| |j2 = - 1j21| -------2---|

Es handelt sich also um eine Parabel.

[prev] [prev-tail] [front] [up]