2.6 Determinanten (Volumenberechnung)

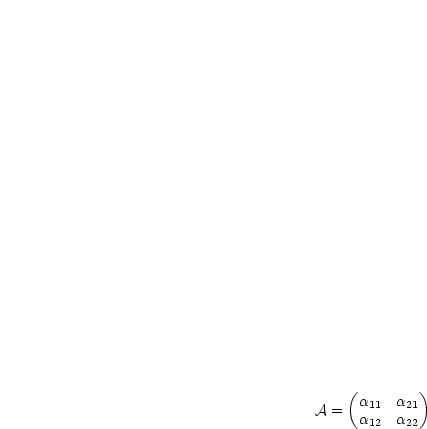
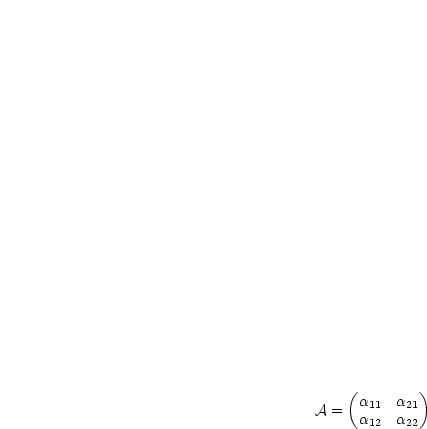
(a11 a21) A = a12 a22

|_ ( ) ( )_ | a11 a21 |_ a12 × a22 _| .e3 = a11a22 - a21a12(= det(A)) 0 0

( ) A = a1,a2,a3

Das Spatprodukt ist definiert durch $(a1× a2).a3(= det(A))$ .

(a1× a2).a3 = a11a22a33+a21a32a13+a31a12a23-a21a12a33-a31a32a13-a11a32a23

2.6.1 Die SARRUS-Regel

(a1× a2).a3 = a11a22a33 + a21a32a13 + a31a12a23 - a21a12a33- a31a32a13- a11a32a23 = = sum (sign(s))a a a s (- S3 (s(1)1)(s(2)2) (s(3)3)

(2.5)

2.6.2 Die Determinantenfunktion

Wir definieren eine Funktion $det$ : $(m,n) C '--> C$ , die einer Matrix eine Determinante zuordnet: $det(A) = det(a1,a2,...,an)$ . Diese Funktion hat die folgenden Eigenschaften:

Forderung 1:
$detEn = 1$
Forderung 2:
:
, ist linear für jedes . Dies bedeutet:
- $fj(x1 + x2) = fj(x1) + fj(x2)$
- $f (cx) = cf (x) j j$
Forderung 3:
$det(..., aj,..., ak ,...) = - det(..., ak,..., aj ,...) j k j k$
$det(a1,a2,...,an) = sign(t)det(a(s(1)),a(s(2))....,a(s(n))$ , $t = (j...k)$

Folgerungen hieraus (Rechnen mit Determinanten):

Aussage 1: $det(cA) = cn det(A),c (- C$
Aussage 2:
$det(A) = 0$ , falls zwei Spalten gleich sind.
$det(A) = -det(A)$ , wenn die gleichen Spalten vertauscht werden.
Aussage 3: $( sum k ) sum k ( ) ( sum k ) det a1,...,aj-1, clnl,aj+1,...,an = cldet a1,..., nl,...,an = fj clnl l=1 l=1 j l=1$
Aussage 4: $A = [a1,...,an],B = [a1,...,aj-1,aj + caj+1,...,an] (l /= j)$
$det(B) = det(A)$ , $det(A)$ verändert sich nicht, wenn zu einer Spalte das Vielfache einer anderen addiert wird. Aus den Aussagen 2 und 3 folgt: $det(B) = det(A)+ det(...,al,...,an)$

Beispiel:

( ) ( ) ( ) 1 1 0 0 1 1 0 0 1 1 0 0 1 0 0 1 1 0 0 1 0 0 0 1 det 0 1 1 0 = det 0 0 1 0 = det 0 0 1 0 = 0 0 0 1 1 0 - 1 1 1 - 1 -1 1 1

2.6.3 Die SARRUSsche Regel

( ) a11 a12 a13 a11 a12 det a21 a22 a23 a21 a22 = a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31- a11a23a32- a12a21a33 = a31 a32 a33 a31 a32 sum = sign(s)a(1s(1))a(2s(2))a(3s(3))

(2.6)

$t (- Sn$ sei Transposition:

det(at1,at2,...,atn = sign(t)det(A)

Beispiel:

Es sei $A$ eine $(3,3)$ -Matrix.

S -) t = (23) det(a ,a a = det(a ,a ,a ) = - det(a ,a ,a) 3 t(1) t(2) t(3) 1 3 2 1 2 3

S3 - ) s = (2,3,1) = t1 o t2

t = (12) 1

t2 = (13)

(12) o (1,2,3) = (2,1,3)

(13) o (2,1,3) = (2,3,1)

(13)o (12)o(1,2,3) = (2,3,1) t t 1 2

Es gilt $f(s) = 2$ , damit liegt folglich eine gerade Permutation vor.

det(a2,a3,a1) = det(as(1),as(2),as(3)) = det(at1ot2(1),at1ot2(2),at1ot2(3)) = - det(a2,a1,a3) = = signt1 det(at2(1),at2(2),at2(3)) = - (1)det(a1,a2,a3) = signt1signt2det(a1,a2,a3) = det(A) sign(t1 o t2) s

(2.7)

Aussagen:

$s (- Sn$ : $det(as(1),as(2),...,as(n)) = sign(s)det(a1,...,an)$
$det(es(1)$ , $es(2),...,es(n)) = sign(s)$
$A (- C(m,n)$ , $r = rang(A) < n$ . Dann gilt det $(A) = 0$ .

Beweis:

sum r sum r det(A) = ± det(b1,...,br,br+1,...,bn)= cjbj = cjdet(b1,...,br,...,bj)= 0 ------------------ j=1 j=1 -------- -------- lineSarpa ulnteanb vho¨anng Aige =0

2.6.4 Der LAPLACEsche Entwicklungssatz

Satz:

$( a1k) a2k sum n A (- C(m,n),A = [a1,...,an] ax = .. = ajkej . j=1 ank$

Es gilt: $sum det(A) = sign(s)as(1),1as(2),2as(3),3as(4),4...as(n),n s (- Sn$

( ) sum n sum n sum n det(A) = det(a1,a2,...,an) = det aj1ej1, aj2ej2,..., ajnejn j=1 j=1 j=1

In Summanden läßt sich dies schreiben als:

n sum sum m sum n ... aj1aj2...ajn det(ej1,...,ejn) j1=1j2=1 jn=1

Es ist $det(ej1$ , $...$ , $ejn) /= 0$ nur dann, wenn $(j1$ , $...$ , $jn)$ eine Permutation aus $Sn$ ist.

sum sum prod n as(1)1as(2)2,...,as(n)nsign(s) = sign(s) = as(j),j s (- Sn s (- Sn j=1

Beispiel:

Es sei $A = [el,a2,a3,a4,...,an]$ mit $el = (dkl)k$ , $a2 = (ak2)k$ , $...$ , $an = (akn)n$ . Der Laplacsche Entwicklungssatz besagt:

sum det(A) = sign(s)ds(1)1as(2)2...as(n)n = Permutation der Zahlen 2, ..., n s (- Sn

( ) det a1,a2,..., el ,ak,...,an = (- 1)k- 1det(e,a ,...,a ,a ,...,a )= k-te Spalte l 1 k-1 k n (1 a11 a12 ... a1k-1 a1k+1 ... a1n) 0 a21 a22 ... a2k-1 a2k+1 ... a2n = (- 1)l-1(-1)k-1det . . . . . . . . .. .. .. .. .. .. .. .. 0 an1 an2 ... ank- 1 ank ... ann

(2.8)

Die $l$ -te Zeile und $k$ -te Spalte von $A$ fehlt. In $A = [a1,...,an]$ streiche $l$ -te Zeile, $k$ -te Spalte. $Alk$ ist $(n - 1,n - 1)$ -Matrix.

det(a1,...,el,ak-1,...,an) = (- 1)k+ldet(Alk)

Betrachten wir folgende konkrete Matrix:

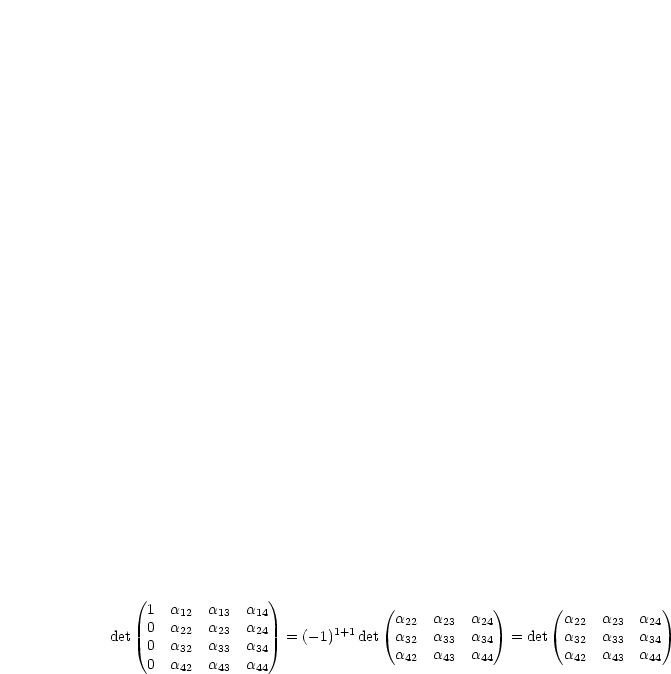
( ) ( ) ( ) 1 a12 a13 a14 a22 a23 a24 a22 a23 a24 det 0 a22 a23 a24 = (-1)1+1 det a32 a33 a34 = det a32 a33 a34 0 a32 a33 a34 a42 a43 a44 a42 a43 a44 0 a42 a43 a44

Satz:

$T det(A) = det(A )$

Übung:

Rechne explizit für $n = 2$ , $3$ , $4$ , $5$ nach.

2.6.5 Der Determinanten-Multiplikationssatz

Satz:

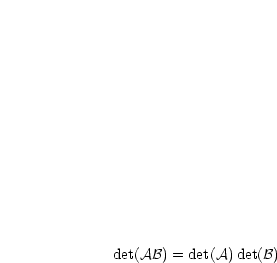$det(AB) = det(A) det(B)$ mit $A$ , $B (- C(n,n)$

Beweis:

Es sei $A = [a1,...,an]$ , $B = [b1,...,bn]$ und $AB = [c1,...,cn]$ . Die Spalten $ck$ der multiplizierten Matrix $AB$ ergeben sich durch Multiplikation der Spalten der Matrix $B$ mit der Matrix $A$ :

sum n ck = Abk = bjkaj j=1

Dann können wir die Determinante berechnen:

( ) sum n sum n sum n sum n sum n det(AB) = det bj11aj1, bj22aj2,..., bjnnajn = ... bj11...bjnndet(aj1,...,ajn) = j1=1 j2=1 jn=1 j1=1 jn=1 sum |-----------| = bs(1)1 ...bs(n)n det(as(1),...,as(n)) = det(B)det(A)-- s (- Sn sign(s)det(A)

(2.9)

Folgerung:

$A (- C(n,n)$ sei regulär. Dann gilt:

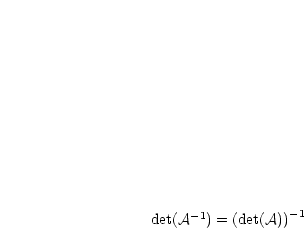
$1 = det(E) = det(AA -1) = det(A) det(A -1)$
$det(A-1) = (det(A))-1$
$A$ sei singulär. $==>$ $det(A) = 0$ $<==>$ $det(A) /= 0$ $==>$ $A$ sei regulär.
$A$ sei regulär. $<==>$ $det(A) /= 0$
$A$ sei singulär. $<==>$ $det(A) = 0$
$Ax = o$ besitzt nichttriviale Lösungen. $<==>$ $det(A) = 0$ (Eigenwertproblem)

2.6.6 Der Entwicklungssatz

Definition:

$A$ sei $(n,n)$ -Matrix. Mit $Ajk$ wird die $(n -1,n - 1)$ -Matrix bezeichnet, die aus $A$ durch Streichen der $j$ -ten Zeile und $k$ -ten Spalte entsteht.

Satz:

Entwicklungssatz der $k$ -ten Spalte und Entwicklungssatz der $k$ -ten Zeile mit $k = 1$ , $2$ , $...$ , $n$ :

$sum n det(A) = ajk(-1)j+kdet(Ajk) j=1$
$sum n det(A) = akj(-1)j+kdet(Akj) j=1$

\text{[math]}

$C(m,n)$ ist unitär, falls $A*A = E$ . $A (- R(m,n)$ heißt orthogonal, falls $ATA = E$ gilt.

Satz:

Es sei $A = R(m,n)$ . Dann sind folgende Aussagen äquivalent:

$A$ ist orthogonal.
$A- 1 = AT$
$A- 1$ ist orthogonal.
$T A$ ist orthogonal.
Die Spalten von $A$ bilden ein Orthonormalsystem.
Die Zeilen von $A$ bilden ein Orthonormalsystem.
$A$ , $B$ sind orthogonal. Dann ist auch $AB$ orthogonal.
Die Menge der orthogonalen Matrizen mit der Matrixmultiplikation bildet eine Gruppe.
$AB$ ist orthogonal, wie auch $B$ . Dann ist $A$ orthogonal.

Beweis von 7.):

(AB)- 1 = B- 1A -1 = BTAT = (AB)T

Beweis von 8.):

Da $B -1$ und $AB$ nach Voraussetzung orthogonal sind, ist auch $A = (AB)B -1$ ist orthogonal. Die restlichen Beweise können als Übung selbst durchgeführt werden.

Für unitäre Matrizen gilt:

$A$ ist unitär.
$A- 1 = A*$
$A- 1$ ist orthogonal.
$* A$ ist orthogonal.
Die Spalten von $A$ bilden ein Orthonormalsystem.
Die Zeilen von $A$ bilden ein Orthonormalsystem.

Beweis:

$A$ ist orthogonal. Damit ist $b1$ , $...$ , $bn$ ein Orthonormalsystem, womit $B = [b1$ , $...$ , $bn]$ orthogonal ist. Das Produkt der beiden ergibt sich durch $AB = [Ab1,...,Abn]$ . $A$ ist außerdem unitär. Daraus folgt der erste Punkt. Ist $b1$ , $...$ , $bn$ ein Orthonormalsystem im $Rn$ , so ist $Ab1$ , $...$ , $Abn$ ein Orthonormalsystem.

$T T x y = (Ax) Ay$ $A$ $x$ , $n y (- R$ $\text{[math]}$ $<x,y> = <Ax$ , $Ay>$ , $x$ , $n y (- C$
$||x|| = ||Ax ||$
$||x- y|| = ||Ax - Ay||$ $A$ $x$ , $y$