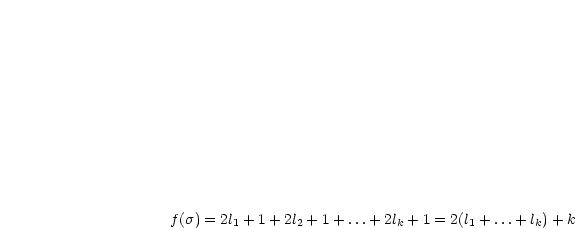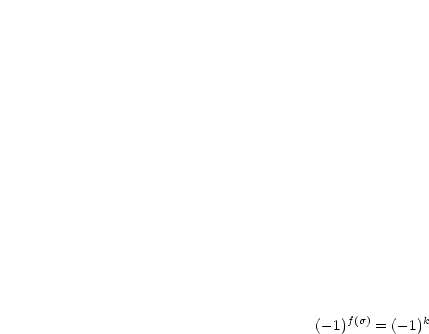heißt Permutation der Zahlen
heißt Permutation der Zahlen  ,
,  ,
,  ,
,  , falls
folgendes gilt:
, falls
folgendes gilt:
 ist eine bijektive Abbildung:
ist eine bijektive Abbildung:  nach
nach  .
.







 bezeichnet alle Permutationen der Zahlen
bezeichnet alle Permutationen der Zahlen  ,
,  ,
,  .
.

 | (2.3) |




Permutationen, die zwei Elemente vertauschen, alle anderen festlassen, heißen Transpositionen.

Es gilt  ,
,  und
und  für
für  ,
,  .
.



Jede Permutation kann als Produkt von Transpositionen geschrieben werden und zwar auf viele Arten.

Es seien  ,
,  .
.




|
Jede Permutation |
|
|
|
Es sei  .
.
 | (2.4) |
|
Jede Darstellung von id |
|
|
Eine Permutation |
|

Zu zeigen: Entweder  und
und  sind gerade, oder
sind gerade, oder  und
und  sind ungerade.
sind ungerade. 
 ist gerade.
ist gerade.


|
Vorzeichen von
|
 , wenn
, wenn  eine Transposition ist.
eine Transposition ist.
 für
für  ,
, 


 ,
,  (Beweis als Übung)
(Beweis als Übung)
|
|
|
 besitze die Fehlstände
besitze die Fehlstände  ,
,  und
und  .
.

|
Ist |
|
Für  definieren wir
definieren wir  .
.