2.4 Regulre Matrizen. Die inverse Matrix zu einer regulren Matrix

2.4 Reguläre Matrizen. Die inverse Matrix zu einer regulären Matrix

Definition:

$A (- C(n,m)$ heißt regulär, falls $rang(A) = n$ gilt.

$( ) 1 ... 0 0 1 0 A = ... ... ... = En,A = [e10,e8,...,e2] 0 ... 0$

(m,n) N (A) = {x|Ax = o},A (- C

rang(A) = r,dimN (A) = n - r

Angenommen, es gibt nur die triviale Lösung:

dimN (A) = 0 = n - r : n = r < m

Ein homogenes Gleichungssystem mit mehr Unbekannten hat außer der trivialen Lösung immer zusätzliche Lösungen.

id:Cn '--> Cn id(x = x A x v1,...,vn u1,...,un

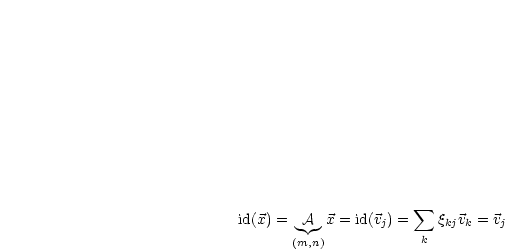
sum id(x) = A x = id(vj) = qkjvk = vj (m,n) k

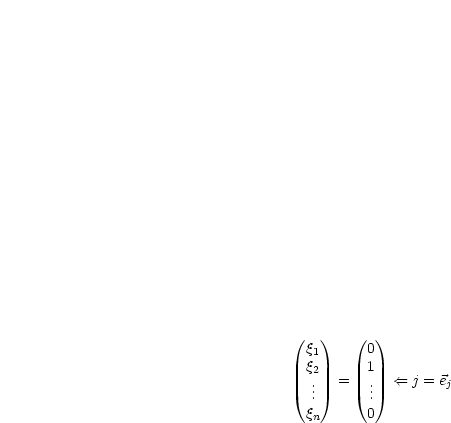
(q1) (0 ) q2 1 . = . <== j = ej .. .. qn 0

A (- C(m,n) : id(x) = Ex

EA = [Ea1,Ea2,...,Ean] = [a1,a2,...,an] = A

AE = [Aa1,...,Aen] = [a1,...,an] = A

Eine $(m, n)$ -Matrix $A$ sei regulär, falls rang $(A) = n$ .

Beispiele: Matrizen, die Zeilenumformungen bewerkstelligen

A regul¨ar <==> AT regul¨ar

Wo werden reguläre Matrizen benötigt?

} A sei regul¨ar und (A (- (m,n) c1Ab1 + c2Ab2 + ...+ cnAbn = o b1,b2,...,bn sei eine Basis. Damit ist Ab1,Ab2,...,Abn Basis. Daraus folgt: c1 = c2 = ...= cn = 0

A(c b + c b + ...+ c b ) = o-A--re-g-ul-¨a-->rc b +c b + ...+ c b = o 1 1 2 2 n n 11 22 n n

Satz:

$A (- C(m,n)$ . Dann gilt:

$A$ ist regulär. $<==>$ $(Ax = o ==> x = o)$ $<==>$ $Ax = y$ ist für jedes $y (- Cn$ eindeutig lösbar.

Satz:

$A$ , $B (- C(m,n)$ ist regulär. Dann ist auch $AB$ regulär.

Beweis:

A regul¨ar B regul¨ar ABx = o = A(Bx) --------> Bx = o --------> x = o

Satz:

$AB$ sei regulär. Dann sind $A$ und $B$ regulär.

Beweis:

$(AB)x = Ao = o A--B-->$ regulär $x = o$ , also ist $B$ regulär. Wenn $CD$ regulär ist, dann folgt daraus, daß der zweite Faktor $D$ regulär ist.

AB regul¨ar <==> (AB)T = BTAT regul¨ar ==> AT regul¨ar ==> A regul¨ar

Satz:

$A$ , $B$ seien reguläre $(m, n)$ -Matrizen. Dann gibt es genau eine reguläre $(m, n)$ -Matrix $X$ mit $AX = B$ . Sei $X = [x ,x ,...,x ] 1 2 n$ .

$AX = B$ $<==>$ $Axj = bj$ für $j = 1$ , $...$ , $n$

Da $A$ regulär ist, ist $xj$ durch $br$ eindeutig bestimmt. Setze $B = E$ , dann heißt die durch $AX = E$ eindeutig festgelegte reguläre die inverse Matrix zu $A$ . Sie wird mit $-1 A$ bezeichnet. Es gilt nun: $-1 AA = E$ .

Es gilt auch: A- 1A = E

A-1 ist regul¨ar: AA -1X = AE = A

EX = A ==> X = A

Satz:

$A$ , $(m,n) B (- C$ seien reguläre Matrizen. Dann gelten:

$(AB)-1 = B-1A -1$ , $(A- 1)-1$ , $(A -1)T = (AT)-1$
$ABX = E$ $==>$ $X = (AB) -1$ , $( ) A BB-1A -1 = AEA - 1 = AA -1 = E$
$- 1 A X = E$ , $T A X = E$ : $T -1 X = (A )$
$AT(A -1)T = (A- 1A)T = ET = E$

Es sei $A = C(m,n)$ regulär. Gesucht ist $A- 1$ . $Z1$ , $Z2$ , $Z3$ seien die reguläre Matrizen, die elementare Zeilenumformungen durchführen.

Z~3 ...Z2Z1 A = E ---Z ----

ZA = E ==> ZAA -1 = EA -1 ==> ZE = A-1

Beispiel:

(1 1 1) A = 2 3 4 3 4 6

| 1 1 1 |1 0 0 2 3 4 |0 1 0 -3--4--6-|0-0--1-- 1 0 0 | 0 1 0 | 0 0 1

Nach einigen Umformungen folgt:

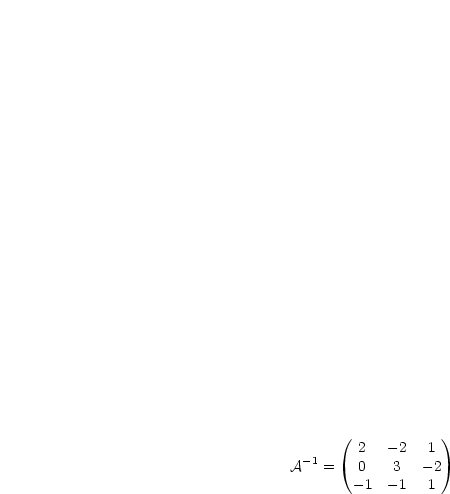
( ) -1 2 - 2 1 A = 0 3 -2 - 1 - 1 1

Wir betrachten die Abbildung $Ax = y$ . Es seien $(m,n) A (- C$ , $n y (- C$ gegeben. $C$ sei regulär und $x '--> Cx$ eine bijektive Abbildung $n n C '--> C$ . Darüber hinaus gilt $' x = Cx$ $A$ $n x (- C$ .

' ' ACx = Cy

c'AC x'= y'==> A'x'= y - ' A

Falls $x$ eine Lösung ist, dann ist auch $x = Cx$ eine Lösung.

( ) a1 ... 0 A = ... 0 0 0 ... an

[next] [prev] [prev-tail] [front] [up]