
 :
:  :
: 
 gegeben („Drehmoment“))
gegeben („Drehmoment“))


Dies sind lineare Abbildungen.

 :
:  :
: 
 gegeben („Drehmoment“))
gegeben („Drehmoment“))


Dies sind lineare Abbildungen.


|
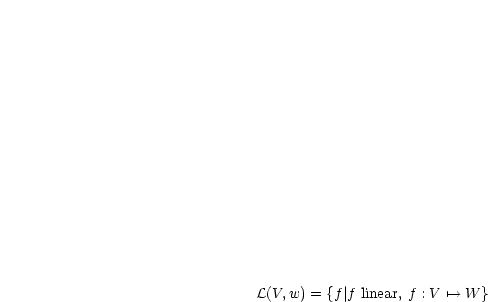
 ,
,  ,
,  :
:

 ,
,  ,
,  ;
;  ,
,  ,
,  :
:

 folgt
folgt  .
.
 ,
,  ,
,  seien Vektorräume.
seien Vektorräume.

Bekannt für  : Zu zeigen für
: Zu zeigen für  .
.
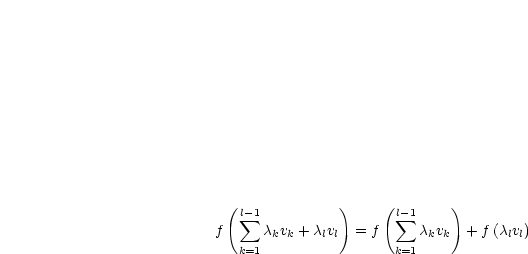
Mit Induktionsvoraussetzung folgt:




 | (2.1) |

 sei
sei  -dimensional:
-dimensional:  sei eine Basis.
sei eine Basis.
 sei
sei  -dimensional:
-dimensional:  sei eine Basis.
sei eine Basis.

 sei Koordinate bezüglich der Basis
sei Koordinate bezüglich der Basis  .
.

 wird genau durch die Bilder der Basisvektoren festgelegt.
wird genau durch die Bilder der Basisvektoren festgelegt.

 ist Koordinatenvektor von
ist Koordinatenvektor von  bezüglich Basis
bezüglich Basis  .
.  ,
,  ,
,  ,
,

 kennzeichnen eindeutig
kennzeichnen eindeutig  .
.

 sind die Zeilen und
sind die Zeilen und  die Spalten der Matrix.
die Spalten der Matrix.  heißt
heißt  -Matrix,
-Matrix,  ist die Menge der
ist die Menge der  -Matrizen.
-Matrizen. ![A = [a1,a2,...,an]](ma719x.gif) nennt man die
Spaltenform der Matrix.
nennt man die
Spaltenform der Matrix.
![( )
1 0 0 ... 0
m,n 0 1 0 ... 0
C -) A = [e1,e2,...,en] = .. .. .. .. .. = En.
. . . . .
0 0 0 ... 1](ma720x.gif)
Diese Matrix heißt Einheitsmatrix.  heißt Diagonalmatrix, falls
heißt Diagonalmatrix, falls  und
und  . Hierfür wird auch geschrieben:
. Hierfür wird auch geschrieben:

Die Schreibweise hat folgende Bedeutung:
 mit
mit 

 ,
,  heißt Nullmatrix.
heißt Nullmatrix.
 ist eine komplexe Zahl.
ist eine komplexe Zahl.
 ist ein Vektor = Spaltenvektor
ist ein Vektor = Spaltenvektor
 :
:  heißt Zeilenvektor.
heißt Zeilenvektor.
|
|
|
|
Ist |
|

Es sei  :
:  mit
mit  , wobei
, wobei  und konstant ist. Es gilt
und konstant ist. Es gilt
 : Wähle kanonische Basis im Urbild und Bild. Gesucht ist
: Wähle kanonische Basis im Urbild und Bild. Gesucht ist
![(3,3)
R - ) A = [a1,a2,a3]](ma756x.gif) .
.




![proja : R3 '--> R3 Gesucht ist (3,3)- MatrixA = [a1,a2,a3]
V '--> W](ma761x.gif)
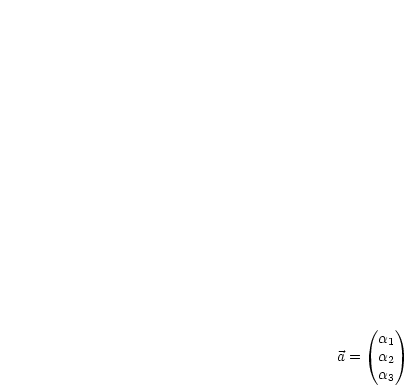
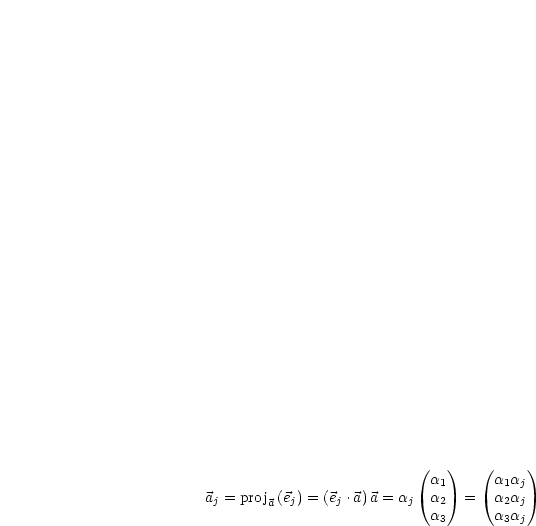



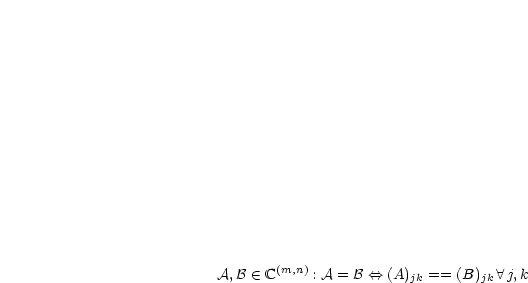
Die Matrix  gehört zur linearen Abbildung
gehört zur linearen Abbildung  ,
,  gehört zu
gehört zu  . Es sei
. Es sei
 und
und  ; dann ist
; dann ist  für
für
 , 2,
, 2,  ,
,  .
.
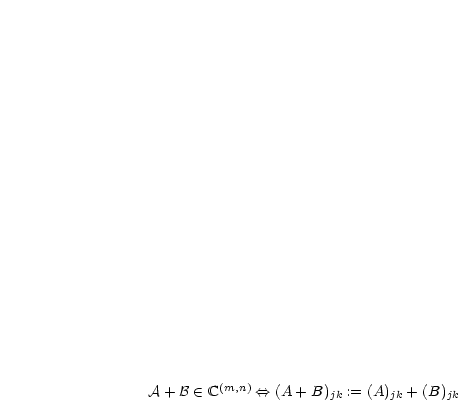
 .
. 

 ,
, 

 .
.





 ,
, 
 ,
,  ,
, 


 heißt hermitesch, falls
heißt hermitesch, falls  , d.h.
, d.h.  für
für  .
.
 heißt symmetrisch, falls
heißt symmetrisch, falls  :
:  für
für  .
.
 heißt schiefsymmetrisch, falls
heißt schiefsymmetrisch, falls  .
.
Es sei  . Dann ist
. Dann ist  symmetrisch:
symmetrisch:

 ist schiefsymmetrisch:
ist schiefsymmetrisch:
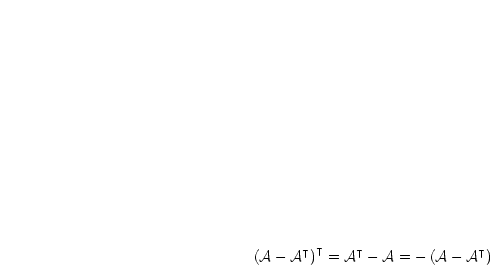
Des weiteren läßt sich  in einen symmetrischen und schiefsymmetrischen Anteil
zerlegen:
in einen symmetrischen und schiefsymmetrischen Anteil
zerlegen:

Diese Vorgehensweise benötigt man bei quadratischen Formen.
![(m,n)
[a1,...,an] = A (- C](ma815x.gif) | ![[ ] (n,l)
b1,...,bl = B (- C](ma816x.gif) |  (Matrixprodukt) (Matrixprodukt) ![AB = [c1,...,cl]](ma818x.gif) |
 |  |  |
 : :  |  : :  |  : :  |



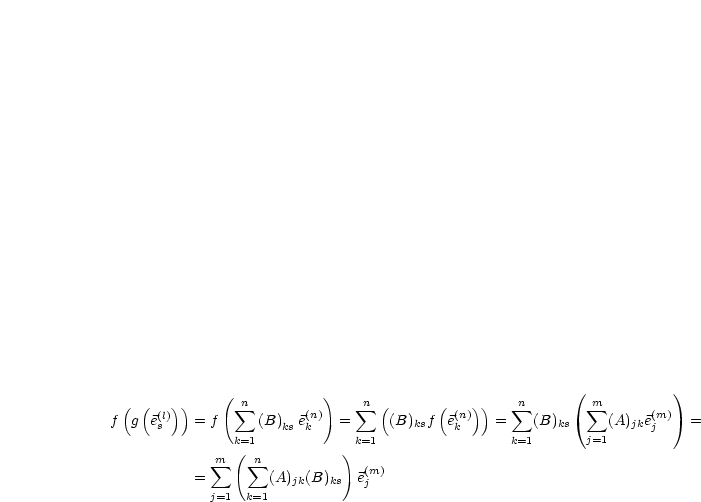 | (2.2) |

|
Ist |
|
|

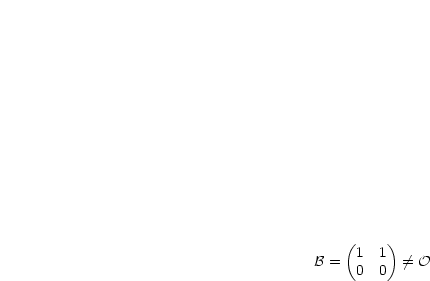
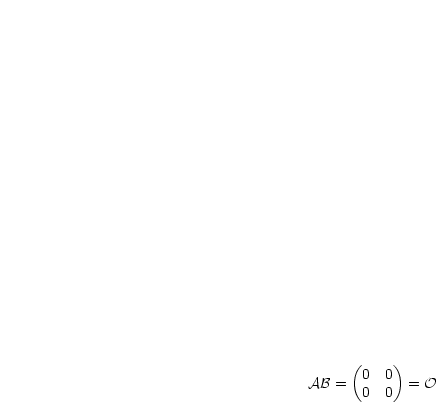

Folglich ist das Matrizenprodukt nicht kommutativ.
 oder
oder 




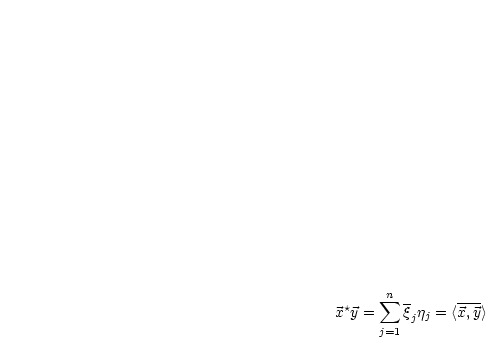
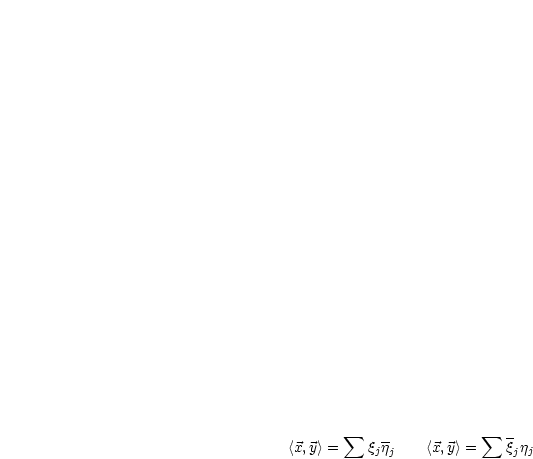



![sum l sum l sum n sum sum
[(AB) C]rs = (AB)rj(C)js = (A)rp(B)pj(C)js = (A)pj (B)pj(C)js = [A (BC)]rs
j=1 j=1p=1 p j](ma861x.gif)

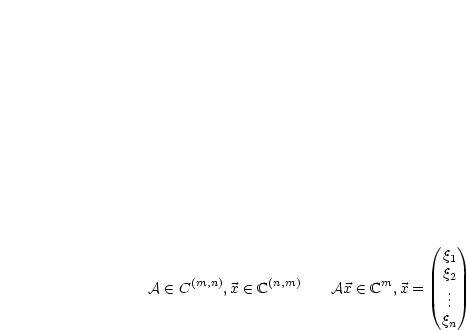
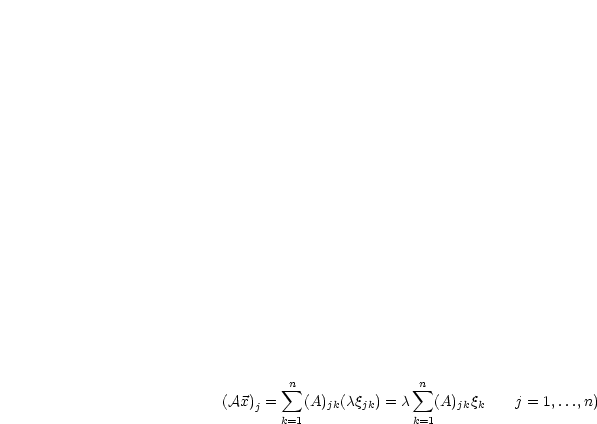




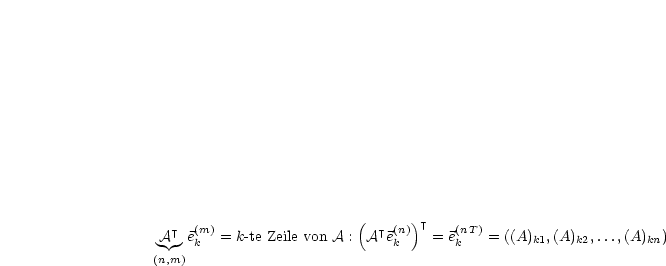
![A = [a,a ,...,a ] (- C(m,n)
1 2 n](ma870x.gif)
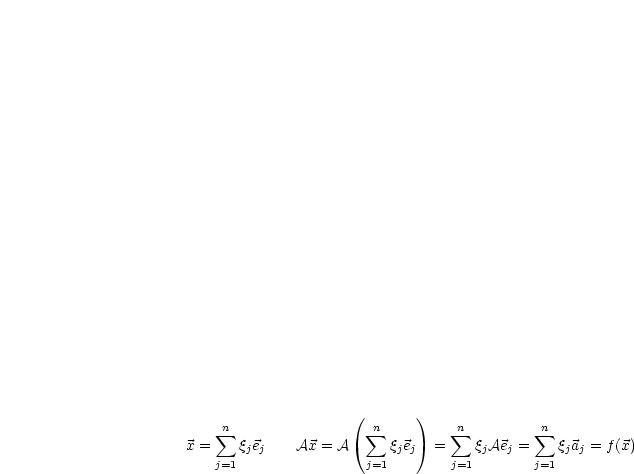



![(1 0 ... 0)
0 1 ... 0
En = [e1,e2,...,en] = . . . .
.. .. .. ..
0 0 ... 1](ma875x.gif)
![[ ]
A = [a1,...,an], B = b1,...,bl AB = C = [c1,c2,...,cl]
(m,n) (n,l)](ma876x.gif)
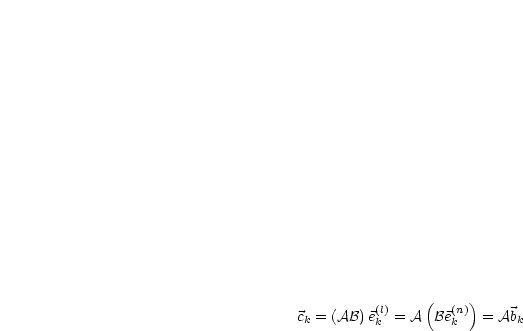
Es kann  als Übung gezeigt werden.
als Übung gezeigt werden.




Dies ist ein lineares Gleichungssystem.
Gegeben ist  -Matrix
-Matrix  und
und  . Gesucht sind
. Gesucht sind  mit
mit
 :
:






 heißt die zugehörige homogene Gleichung.
heißt die zugehörige homogene Gleichung. 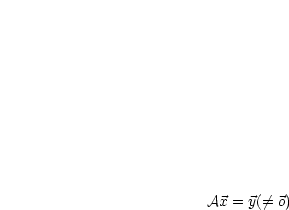 ist die
inhomogene Gleichung.
ist die
inhomogene Gleichung.




![(A,y) = [a1,a2,...,an,y]
(m,n+1)](ma900x.gif) beinhaltet die Informationen, die gegeben sind.
beinhaltet die Informationen, die gegeben sind.
|
|
|
Folgerung: |
Achtung: Daraus, daß |
|
Unter dem Rang einer Matrix versteht man:
Durch elementare Zeilenumformungen werden der Rang einer Matrix  und die
Lösungsgesamtheit des Gleichungssystems
und die
Lösungsgesamtheit des Gleichungssystems  nicht verändert.
nicht verändert.


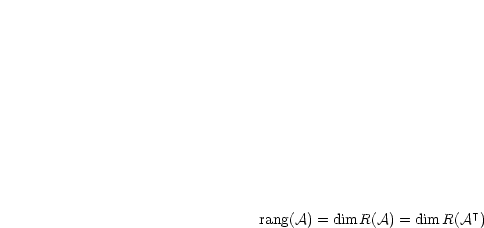
Wir betrachten  . Es sei
. Es sei  ,
,  und
und  gesucht.
Nimm
gesucht.
Nimm  :
:



 ist nicht lösbar, falls
ist nicht lösbar, falls 

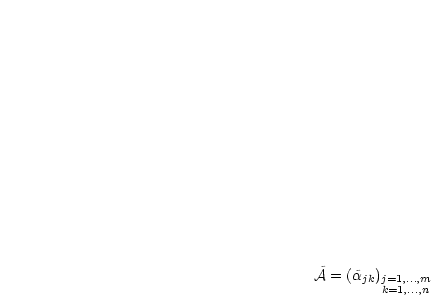
Jeder Vektor  , für den
, für den  ,
,  ,
,  Lösung von
Lösung von  .
.
|
Gegeben sind |
|
|
|
 =?
=?  erfüllt man wie folgt: Setze
erfüllt man wie folgt: Setze  , wobei
, wobei  ,
,  ,
,
 ,
,  und berechne
und berechne  ,
,  ,
,  aus der Zeilennormalform.
aus der Zeilennormalform.

 ,
,  ,
,  werden wie folgt bestimmt. Setze in (ZN)
werden wie folgt bestimmt. Setze in (ZN)
 .
.
 Koordinaten jedes Lösungsvektors, die auf der rechten Seite
von (ZN) stehen, können beliebig gewählt werden; die
Koordinaten jedes Lösungsvektors, die auf der rechten Seite
von (ZN) stehen, können beliebig gewählt werden; die  ,
,  ,
,  sind dann durch (ZN) festgelegt. Setze der Reihe nach eine der frei
wählbaren Koordinaten gleich 1 und alle anderen gleich Null und berechne
jeweils
sind dann durch (ZN) festgelegt. Setze der Reihe nach eine der frei
wählbaren Koordinaten gleich 1 und alle anderen gleich Null und berechne
jeweils  ,
,  ,
,  aus (ZN). Auf diese Weise erhält man
aus (ZN). Auf diese Weise erhält man  linear unabhängige Lösungen des homogenen Problems.
linear unabhängige Lösungen des homogenen Problems.
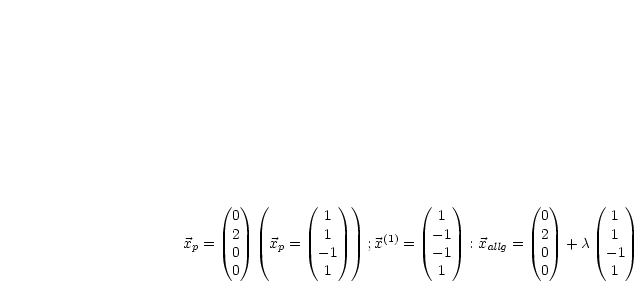
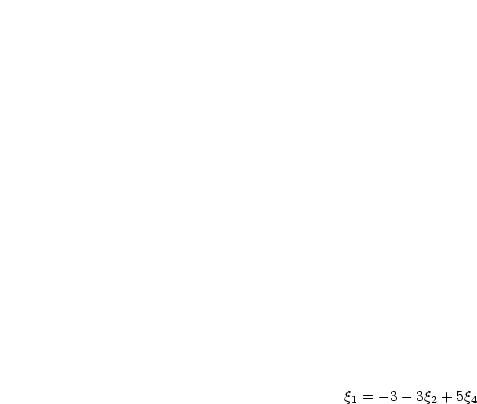



|
|
Aus |
|
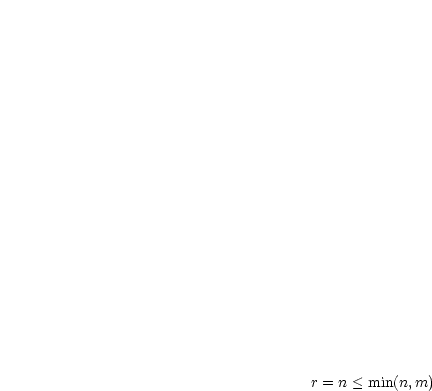
Die Voraussetzung des Satzes sind nur möglich, falls  oder
oder  ist.
ist.
|
Ein homogenes Problem mit mehr Unbekannten als Gleichungen |
|
Es sei  und
und  ,
,  ,
,  ,
,  :
:  .
Daraus folgt
.
Daraus folgt  , das heißt:
, das heißt:  ,
,  ,
,  sind linear
abhängig.
sind linear
abhängig.
|
|

Setze in (1) 




 ,
,  ,
,  sind linear unabhängig:
sind linear unabhängig:


 ,
,  ,
,  linear unabhängig sind. Daraus
folgt, daß
linear unabhängig sind. Daraus
folgt, daß  ,
,  ,
,  Basen in
Basen in  sind. Jedes
sind. Jedes  besitzt eine
eindeutige Darstellung
besitzt eine
eindeutige Darstellung 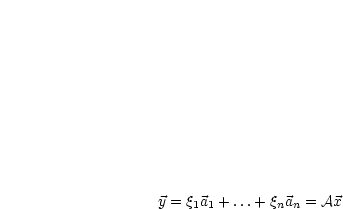 . Ziel:
. Ziel:  besitzt
genau eine Lösung für jedes
besitzt
genau eine Lösung für jedes  .
.