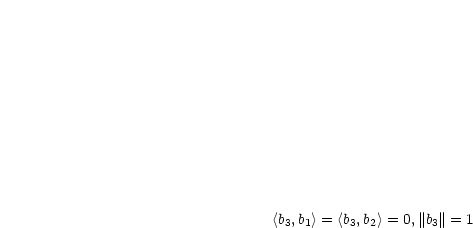,
,  sei Vektorraum, heißt Untervektorraum (Teilraum) von
sei Vektorraum, heißt Untervektorraum (Teilraum) von  , falls
gelten:
, falls
gelten:
 ,
,  sei Vektorraum, heißt Untervektorraum (Teilraum) von
sei Vektorraum, heißt Untervektorraum (Teilraum) von  , falls
gelten:
, falls
gelten:
 ,
, 


 ,
, 


 ,
,  ist Teilraum von
ist Teilraum von  .
.
 ist Teilraum von
ist Teilraum von  .
.
 :
:  ,
, 
Ist dies ein Unterraum? Nein, es sei denn  .
.

 ,
,  :
: 
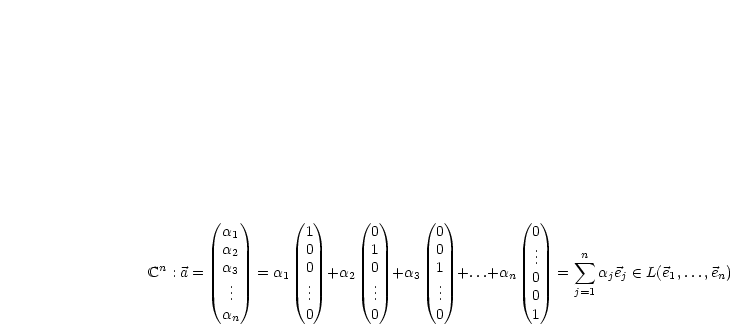


 sei Vektorraum:
sei Vektorraum:  ,
,  ,
,  heißen linear unabhängig, falls aus
heißen linear unabhängig, falls aus
 folgt
folgt  .
.
Folgende Vektoren  sind linear unabhängig:
sind linear unabhängig:

 sei Vektorraum:
sei Vektorraum:  ,
,  ,
,  heißen linear abhängig, falls die nicht
linear unabhängig sind, d.h. es gibt:
heißen linear abhängig, falls die nicht
linear unabhängig sind, d.h. es gibt:

Auch sind folgende Vektoren  linear unabhängig:
linear unabhängig:
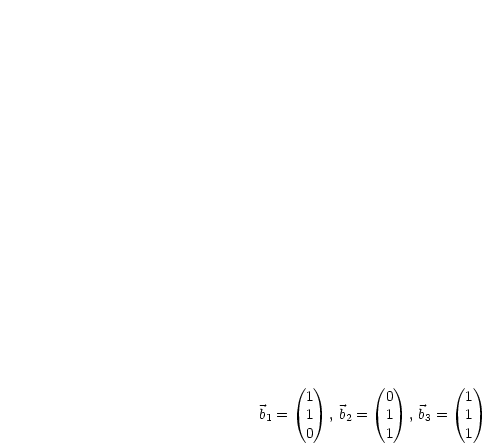
Wir betrachten außerdem  .
.  ,
,  ,
,  und
und  sind dann linear
abhängig:
sind dann linear
abhängig:
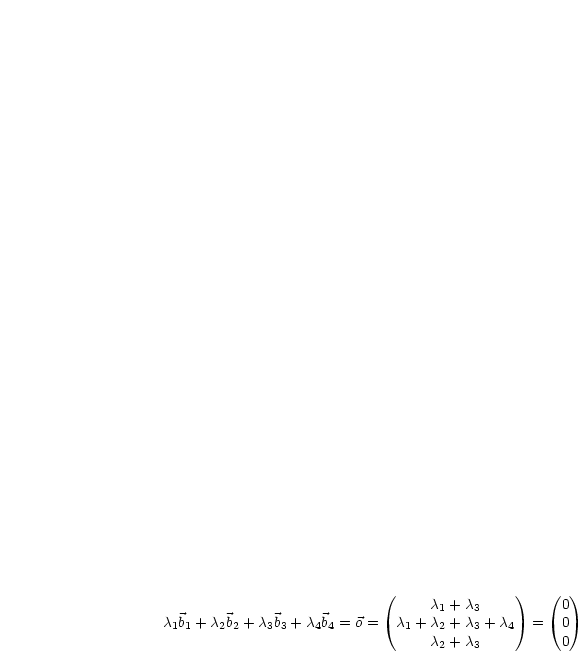


Drücke  durch
durch  aus. Sind
aus. Sind  ,
,  ,
,  ,
,  linear abhängig, so
heißt das:
linear abhängig, so
heißt das:  , wobei mindestens
, wobei mindestens  . Es sei etwa
. Es sei etwa
 . Damit ergibt sich
. Damit ergibt sich  , das heißt:
, das heißt:  ,
,  ,
,
 ,
,  =
= ,
,  ,
,  . {
. { ,
,  ,
,  sind linear abhängig, falls ein
Vektor der Nullvektor
sind linear abhängig, falls ein
Vektor der Nullvektor  ist.
ist.
Eine Basis (Koordinatensystem) in einem Vektorraum  ist eine Menge
ist eine Menge  von
Vektoren mit folgenden Eigenschaften:
von
Vektoren mit folgenden Eigenschaften:

 ist linear unabhängig.
ist linear unabhängig.
Der Vektorraum heißt endlich dimensional, wenn es eine endliche Basis gibt. Der
Vektorraum ist unendlich dimensional, wenn es zu jedem  n linear
unabhängige Vektoren gibt.
n linear
unabhängige Vektoren gibt.

Diese nennt man kanonische Basis, natürliche Basis, Standardbasis.
 ,
,  ,
,  sind linear unabhängig.
sind linear unabhängig.


 :
:  ,
, 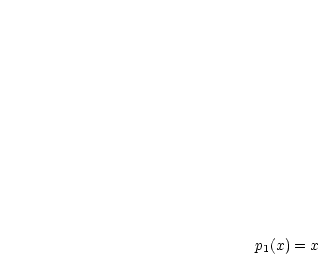 ,
,  ,
,  sind Basis in
sind Basis in  .
.


Wie kann man das zeigen?
Setze vier  -Werte ein und berechne
-Werte ein und berechne 
Man kann auch nacheinander differenzieren und  -Werte einsetzen.
-Werte einsetzen.

|
Es sei |
|
|
|
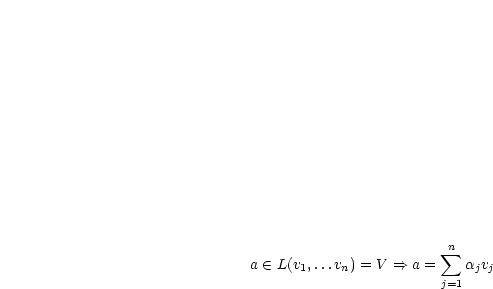
Zu überprüfen ist, daß aus  folgt
folgt  ,
,  ,
,  ,
,
 .
.

 ,
,  ,
,  ,
, 

 ,
,  ,
,  ,
,  ,
,  sind linear abhängig.
sind linear abhängig.

 :
:
 gegeben durch:
gegeben durch:
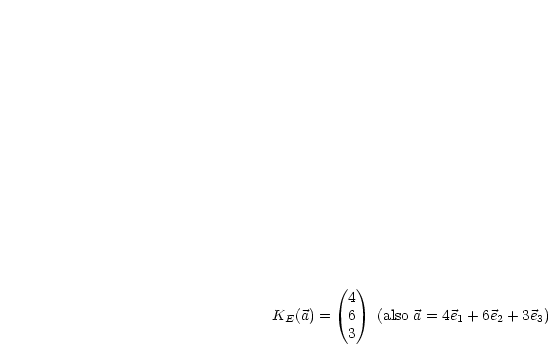

 ,
,  und
und  sind gesucht:
sind gesucht:



 ist injektiv und surjektiv.
ist injektiv und surjektiv.
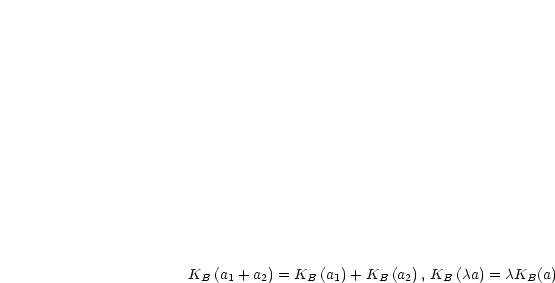
|
Es sei |
|
|
Wir nehmen an, daß  ,
,  ,
,  linear unabhängig sind:
linear unabhängig sind:
 . Ist etwa
. Ist etwa  :
:


|
Es seien |
|
 und
und  wird mit vorhergehendem Satz ausgeschlossen. Daraus ergibt
sich
wird mit vorhergehendem Satz ausgeschlossen. Daraus ergibt
sich  .
.
Wir erinnern uns:


|
Es sei 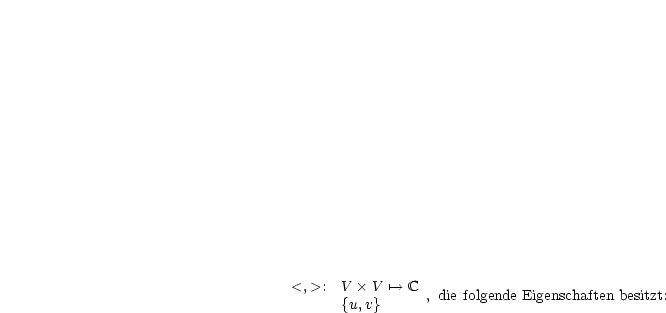
|
Es ist zu zeigen, daß  ein Skalarprodukt auf
ein Skalarprodukt auf  ist.
ist.


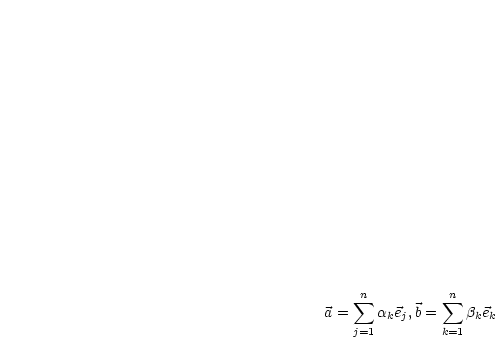
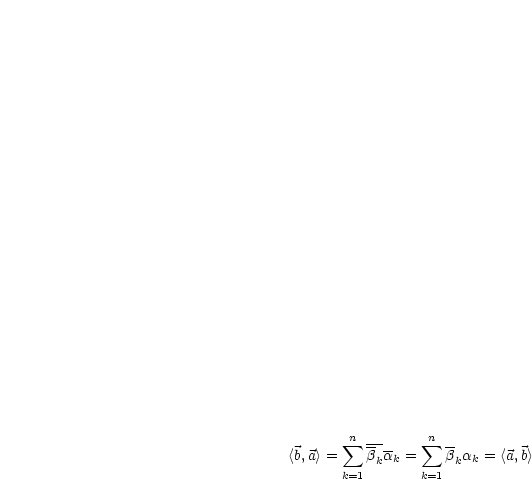

![1
integral ----
C[0,1] : <f,g> = f(x)g(x)dx
0](ma568x.gif)
 ist sowohl stetig als auch komplex.
ist sowohl stetig als auch komplex.

Betrachten wir die  -periodische Funktion aus
-periodische Funktion aus ![C[- p,p]](ma572x.gif) :
:

Ein komplexer Vektorraum  mit Skalarprodukt
mit Skalarprodukt  heißt unitärer Raum. Ein
reeller Vektorraum mit Skalarprodukt heißt euklidischer Raum.
heißt unitärer Raum. Ein
reeller Vektorraum mit Skalarprodukt heißt euklidischer Raum.
|
|

![1 1
| integral 1 ---- | ( integral 1 ) 2 ( integral 1 ) 2
C[0,1] :|| f(x)g(x)dx||< |f (x)|2dx |g(x)|2dx
0 0 0](ma591x.gif)
In einem unitären Raum heißen  ,
,  orthogonal zueinander, falls
orthogonal zueinander, falls  gilt.
gilt.



|
|
|
Es sei |
|

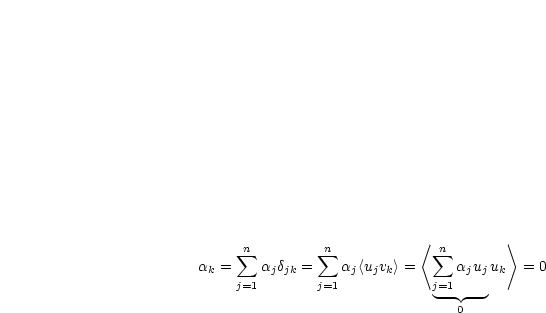
 :
:

![ikx
In C[- p,p] : ek(x) = e](ma621x.gif)


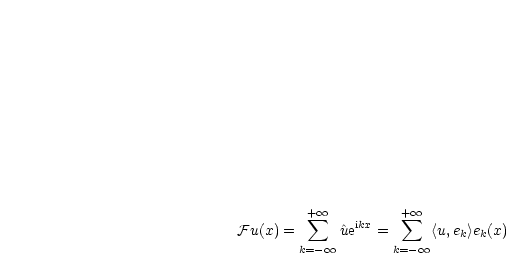
Aufgaben 2/4: Übergang von einer Basis zu einer Orthonormalbasis
|
In einem unitären Vektorraum
|