

Für  handelt es sich um ebene Kurven, für
handelt es sich um ebene Kurven, für  sind es sogenannte
Raumkurven.
sind es sogenannte
Raumkurven.
|
|
Eine stetige Abbildung |
|
|

Es handelt sich um einen Halbkreis auf der rechten Halbebene.


Dies ist eine Ellipse auf der rechten Halbebene.

Dies ist eine andere Darstellung für  .
.

Die Umkehrfunktion  wird damit dargestellt.
wird damit dargestellt.


Es handelt sich hier um eine sogenannte ARCHIMEDESsche Spirale.
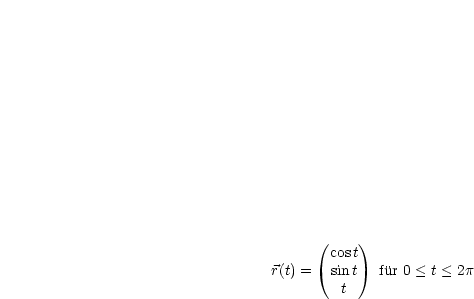
Die Kurve stellt eine Schraubenlinie mit gleichbleibender Ganghöhe dar.
|
Im |
|
|
|

|
Durch eine Parameterdarstellung wird |
|

 :
:  ist Doppelpunkt.
ist Doppelpunkt.


 ist Doppelpunkt.
ist Doppelpunkt.

Es ist der obere Halbkreis.

Auch hiermit wird der obere Halbkreis dargestellt.
|
|
Eine bijektive stetige Abbildung |
|
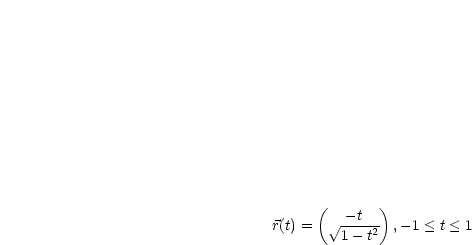

Durch Koordinatentransformation erhält man:


Eine Raumdiagonale wird dargestellt durch:



Dies ist dieselbe Raumdiagonale.