3.1 Kurven im

3.1.1 Parametertransformation
3.2 Differentiation von Kurven

3.2.1 Bogenlänge (Länge
 einer glatten Kurve
einer glatten Kurve  )
)
3.2.2 Die natürliche Darstellung einer Kurve
3.3 Differenzieren von Funktionen mit mehreren Veränderlichen
3.3.1 Richtungsableitung/Partielle Ableitung
3.3.2 Vektoranalysis
3.3.3 Ebene Polarkoordinaten
3.3.4 Räumliche Polarkoordinaten (Kugelkoordinaten)
3.4 Nabla-Kalkül
3.4.1 Der Gradient
3.4.2 Die Divergenz
3.4.3 Die Rotation
3.4.4 LAPLACE-Operator
3.5 Differenzieren von Funktionen

3.5.1 Differenzierbarkeitskriterium
3.5.2 Kettenregel
3.5.3 Parameterdarstellung einer Fläche
 in
in 
3.5.4 Anwendung der Kettenregel (Differentiation von Parameterintegralen)
3.6 TAYLORformel
3.7 Relative (Lokale Extremwerte)
3.7.1 Extremwerte von Funktionen, die auf abgeschlossenen und beschränkten Bereichen definiert sind
3.8 Inverse und implizite Funktionen
3.8.1 Inverse Funktionen
3.8.2 Implizite Funktionen (Mehr Unbekannte als Gleichungen)
3.9 Extremwertaufgaben mit Nebenbedingungen (NB)
 :
:  und
und  eine
eine  -Matrix.
-Matrix.
 .
.

 skalare Gleichungen
skalare Gleichungen 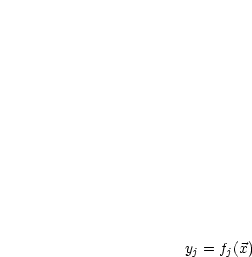 , wobei
, wobei  , 2,
, 2,  ,
, 
 ist stetig in
ist stetig in  , falls aus
, falls aus  (
( ist eine Folge
ist eine Folge  )
folgt:
)
folgt:  .
.  sei eine Folge von Vektoren:
sei eine Folge von Vektoren:

 heißt:
heißt:  für
für  ,
,  ,
,  ,
,  ,
, 


 ist stetig in
ist stetig in 
 Jede Koordinatenfunktion
Jede Koordinatenfunktion  ist in
ist in  stetig.
stetig. ist in
ist in  stetig, falls es zu jedem
stetig, falls es zu jedem  ein
ein  derart gibt, daß aus
derart gibt, daß aus  mit
mit  folgt
folgt 
 in
in  unstetig ist?
unstetig ist?
 sei
sei  -Matrix,
-Matrix,  ,
,  ist stetig auf
ist stetig auf 

 für
für  : Gilt dann
: Gilt dann  für
für  , 2,
, 2,
 ,
,  ?
?

 :
: 
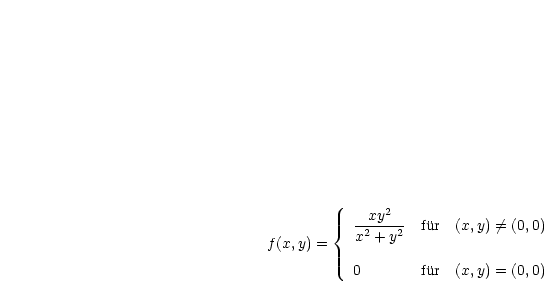
 ist in
ist in 
 für
jedes Folge
für
jedes Folge 
 Gerade durch
Gerade durch  , dann gilt
, dann gilt  für
für

 :
: 


 ist stetig für alle
ist stetig für alle  . Existiert
. Existiert  ? Wenn ja, wird
dieser Wert als Wert für
? Wenn ja, wird
dieser Wert als Wert für  gewählt. Wir untersuchen die Funktion
komponentenweise:
gewählt. Wir untersuchen die Funktion
komponentenweise:
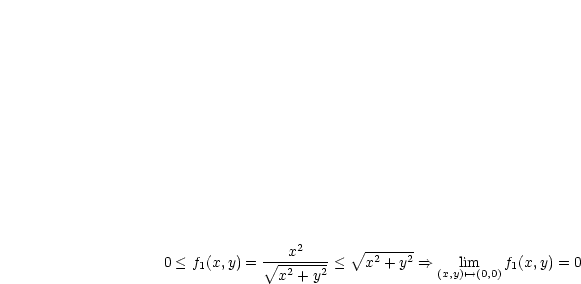



 in
in  stetig.
stetig.
 mit
mit  ist
ist 
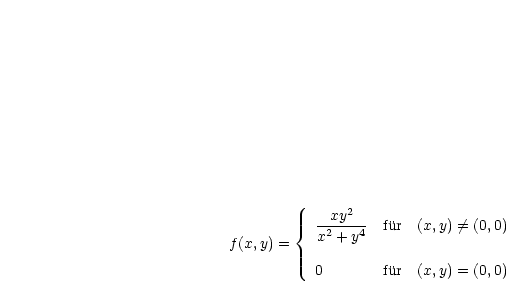
 nicht existiert.
nicht existiert.