3.4 Nabla-Kalkl

[next] [prev] [prev-tail] [tail] [up]

3.4 Nabla-Kalkül

3.4.1 Der Gradient

Das Symbol für den Gradienten ist $\~/$ . $\~/$ ist ein sogenannter Vektoroperator.

( D1) (D1f ) D2 D2f \~/ = . \~/ f (x) = . (x) .. .. Dn Dnf

\~/ : Skalarfeld '--> Vektorfeld f : D (_ Rn '--> R \~/ f : D (_ Rn '--> Rn

3.4.2 Die Divergenz

$\~/ f (x)$ heißt Gradient von $f$ in $x =$ grad $f(x)$ .

T sum n \~/ .f(x) = \~/ f(x) = Djfj(x) j=1

\~/ T : Skalarfeld '--> Vektorfeld n n sum n f : D (_ R '--> R j=1Djfj(x) = divf(x)

3.4.3 Die Rotation

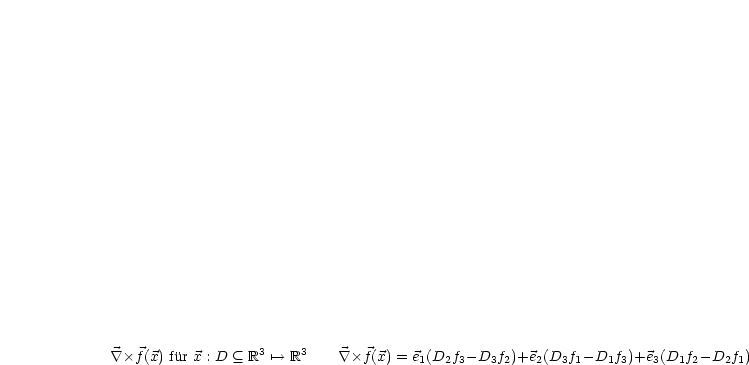
3 3 \~/ × f(x) f¨ur x : D (_ R '--> R \~/ ×f(x) = e1(D2f3- D3f2)+e2(D3f1-D1f3)+e3(D1f2 -D2f1)

3.4.4 LAPLACE-Operator

( ) \~/ T\ ~/ f(x) = div gradf (x) = \~/ T \~/ f (x) = (D2 + D2 + ...+ D2)f (x) --1----2 ------n- /_\ = \~/ T\ ~/ = \~/ . \~/

aTb = bTa \~/ Tf /= fT \~/

Beispiel:

Für ein Skalarfeld gilt:

f,g : Rn '--> R f .g : Rn '--> R |, |, \~/ (fg) \~/ (f g)

\~/ (f g) = \~/ (fg) + \~/ (fg) = g \~/ f + f \~/ g

Für ein dreidimensionales Vektorfeld erhalten wir:

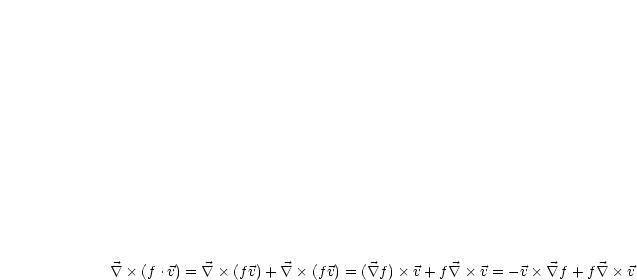
\~/ × (f .v) = \~/ × (fv)+ \~/ × (fv) = ( \~/ f )× v+ f \~/ × v = -v× \~/ f +f \~/ ×v

\~/ T(f v) = \~/ T(fv)+ \~/ T(f v) = vT( \~/ f) +f \~/ Tv

Problem:

Kugelkoordinaten:
Welches Gebilde wird durch $h = p4$ beschrieben? Es handelt sich wohl um einen Kegel mit dem Öffnungswinkel $p2$ .
- $p f = const. = 4$ : Beschreibung einer Ebene
- $r = const.$ : Kugeloberfläche
Ebene Polarkoordinaten:
- $r = const.$ : Kreis
- $f = const.$ : Halbgerade

Beispiel:

(x1) ( ) v(x) = x = x2 \~/ × v (x) x3

( \~/ .v)(x) = n

( V~ ---------------) f(x) = g(||x||) = g x2+ x2 +...+ x2 kugelsymmetrisch 1 2 n

( -x1) ||xx||2 ||x|| -x- h(x) = ||x||, \~/ h(x) = ... = ||x|| -xn ||x||

' -x- f(x) = g(|| x||) : \~/ f(x) = g (||x||)||x||

( ) f(x) =-1- : \~/ f (x) = --1-.x--= - -x-- g(t) = 1- ||x|| ||x||2 ||x ||x||2 t

x ( ) 1 ( 1 ) n -x n- 1 ~f(x) = ||x-||: \~/ .f (x) = ||x|| \~/ .x+ x. \~/ ||x|| = ||x|| + x. ||x||= ||x||--

( ) x n - 1 /_\ ( ||x||) = \~/ . \~/ ( ||x||) = \~/ .||x|| =-||x||

( ) ( ) f(x) = g(||x||) : /_\ f (x) = \~/ . \~/ f (x) = \~/ . g'(||x||).-x =-x . \~/ g'(||x||)+ g'(||x||) \~/ .-x = ||x|| ||x|| ||x|| -x- '' -x- ' n--1- '' n---1 ' = ||x|| .g (|| x ||).||x|| +g (||x||). ||x|| = g (||x||)+ ||x|| g(||x||)

(3.3)

Satz:

$f : R3 '--> R : v : R3 '--> R3$ : Alle partiellen Ableitungen 2.Ordnung mögen existieren und stetig sein.

Dan gelten:

$( ) \~/ × \~/ f (x) = o rot gradf = o$
$( ) \~/ . \~/ × v (x) = 0 div rot v = 0$
$( ) ( ) \~/ × \~/ × v (x) = \~/ \~/ .v (x)- /_\ v(x)$
$( ) ( ) ( ) ( ) a× b × c = (a.c)b- a .b c : \~/ × \~/ × v = \~/ \~/ .v - /_\ v$

[next] [prev] [prev-tail] [front] [up]