
Wir betrachten fortan folgende Funktionen:

Eine solche Funktion nennt man für  Vektorfeld, für
Vektorfeld, für  handelt es sich
um ein sogenanntes Skalarfeld. Kraftfelder und elektrische Felder sind beispielsweise
Vektorfelder. Temperaturfelder sind Skalarfelder.
handelt es sich
um ein sogenanntes Skalarfeld. Kraftfelder und elektrische Felder sind beispielsweise
Vektorfelder. Temperaturfelder sind Skalarfelder.
Zuerst führen wir eine Vorbetrachtung zur Motivation durch:




Gegeben ist  (in Definitionsbereich von
(in Definitionsbereich von  und eine
Richtung
und eine
Richtung  im
im 

|
|
|
|
|
Dann ist |
|
|
|

Ist  , so wächst
, so wächst  bei
bei  in Richtung
in Richtung  . Wenn
. Wenn  ist, so fällt
ist, so fällt  bei
bei  in Richtung
in Richtung  .
.
|
|
|
|
|




 sei konstant.
sei konstant.
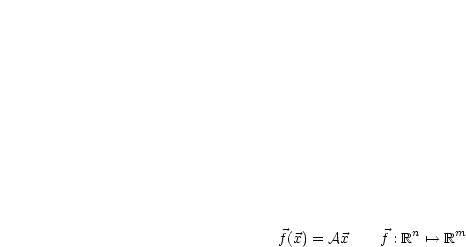
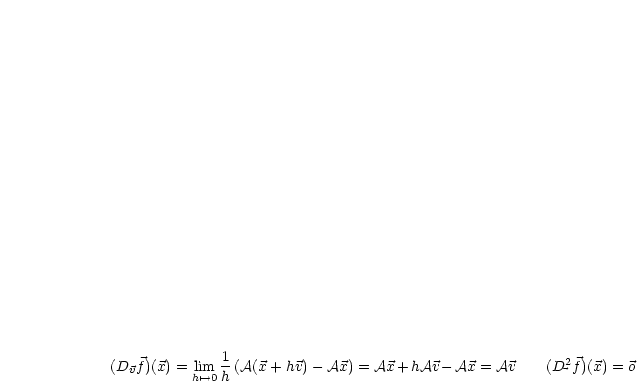

|
|
|
|
|
Wir berechnen:
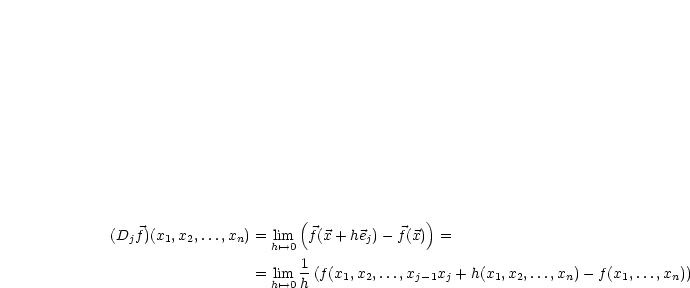 | (3.1) |
Es werden die Variablen  ,
,  ,
,  ,
,  ,
,  ,
,  festgehalten; die
übrigbleibende Funktion von
festgehalten; die
übrigbleibende Funktion von  wird wie in HM I differenziert.
wird wie in HM I differenziert.
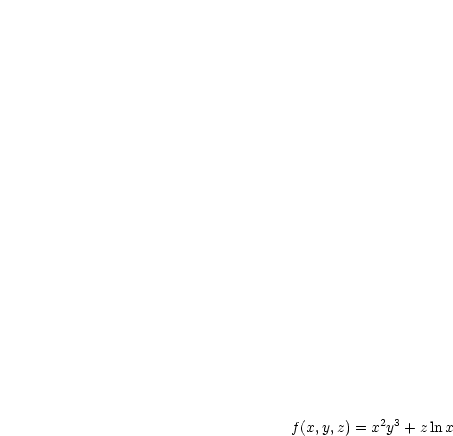

Die partiellen Ableitungen  ,
,  ,
,  können als Übung berechnet
werden.
können als Übung berechnet
werden.

 ist nicht stetig in (0,0).
ist nicht stetig in (0,0).

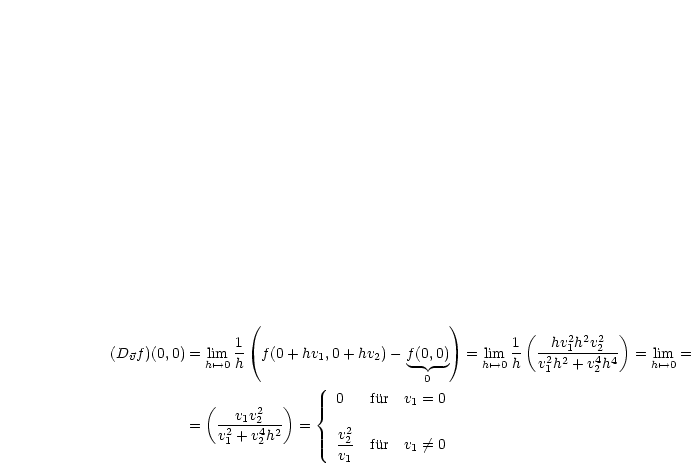 | (3.2) |
 ist im Punkt
ist im Punkt  in jeder Richtung
in jeder Richtung  differenzierbar, also auch partiell
differenzierbar.
differenzierbar, also auch partiell
differenzierbar.
Es gilt  an der Stelle
an der Stelle  .
.
|
Aus der Existenz der Richtungsableitungen an einer Stelle für jede Richtung darf nicht auf Stetigkeit geschlossen werden. |
|

 ,
,  bleiben konstant, differenziere nach
bleiben konstant, differenziere nach  wie gelernt:
wie gelernt: 

Außerdem gilt hier:  , was in folgendem Satz
verallgemeinert wird.
, was in folgendem Satz
verallgemeinert wird.
|
Die Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
Falls |
|




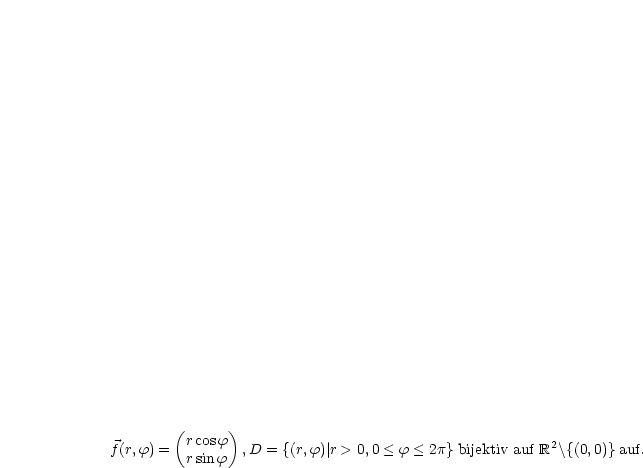





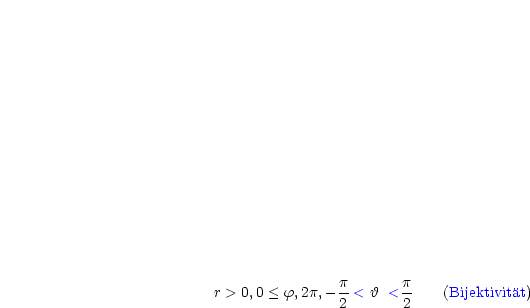


Wir entwickeln nach der letzten Zeile und erhalten:

