3.2 Differentiation von Kurven r : I <img src="cmsy10-1a.gif" alt="<" class="10x-x-1a" /> <img src="msbm10-52.gif" alt="R" class="10x-x-52" /> '<img src="cmsy10-21.gif" alt="-->" class="10x-x-21" /> <img src="msbm10-52.gif" alt="R" class="10x-x-52" />m

3.2 Differentiation von Kurven $m r : I < R '--> R$

$r = f : IRm '--> R$ heißt in $x0$ differenzierbar, falls es einen Vektor $a (- Rm$ und eine in $x0$ stetige Funktion $f : I '--> Rm$ gibt mit:

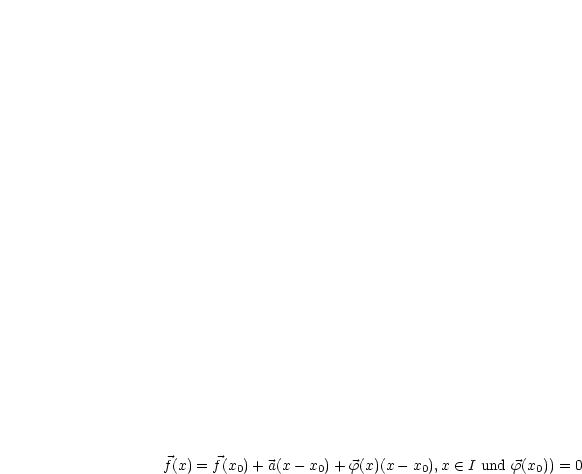
f(x) = f(x0) +a(x - x0)+ f(x)(x - x0),x (- I und f(x0)) = 0

In diesem Fall ist $a$ eindeutig bestimmt, $a$ wird mit $f'(x0)$ bezeichnet.

( ) f(x)--f(x0) lxim'-->x0(a+-f(x))= xli'-->mx0 x- x0 a

Ist $r : I '--> Rm$ in $t0 (- I$ differenzierbar, so gilt:

r(t) = r(t0)+-r'(t0)(t--t0)+f(t)(t- t0) ,f ist stetig, f(t0) = 0 g(t)

$g(t)$ ist Parameterdarstellung einer Geraden, die in einer Umgebung von $r(t0)$ die Kurve $r(t)$ in dem Sinne „gut “ approximiert, daß

||r(t)- g(t)|| lit'-->mt -----------= 0 0 t -t0

$f(t)$ beschreibt die Tangente $r = r(t)$ in $r(t0)$ , falls $r'(t0) /= o$ :

{ -t--t0- } g(t) = t1li'-->mt0 r(t0)+ t1- t0 (r(t1)- r(t0))

Erinnerung (HM I):

Betrachten wir den Spezialfall $n = 2$ :

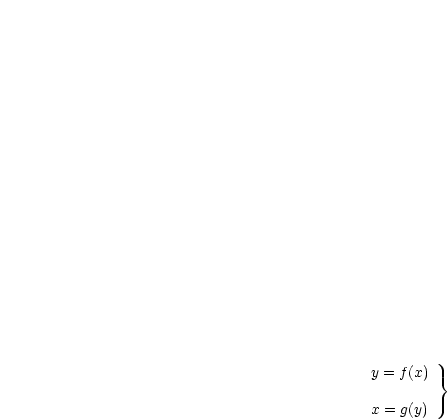
Explizite Kurvendarstellung: $y = f(x) } x = g(y)$
Parameterdarstellung: $(x(t)) r = r(t) = y(t) f¨ur t (- I$
Implizite Darstellung: $x2 y2 a2 + b2 = 1$
Darstellung als Schnitt von zwei Flächen ( $n = 3$ ): $z = x2 + y2 } x + y+ z = 1$

Beispiel:

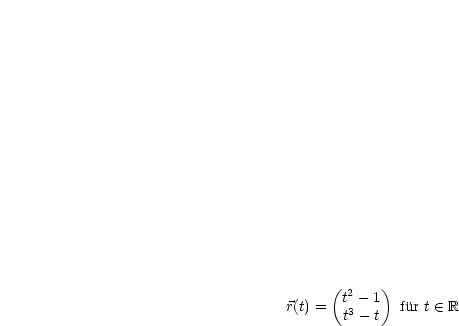
( 2 ) r(t) = t3- 1 f¨ur t (- R t - t

Betrachten wir die implizite Darstellung:

2 } t eliminieren x = t3 - 1 ------ ----> x3 + x2 = y2 y = t - t

r(- 1) = r(1) = o

( ) - 1 t = 0 : r(0) = 0

( ) ' 2t r (t) = 3t2 - 1

' (- 2) ' (2) ' ( 0 ) r(- 1) = 2 ,r (1) = 2 ,r(0) = - 1

Satz:

$( ) q1(t) q2(t) r = r(t) = .. . qn(t)$ ist in $t0$ differenzierbar.

Jede Koordinatenfunktion $q k$ : $I '--> R$ ist in $t 0$ differenzierbar, und es gilt: $( ' ) q1'(t0) r'(t) = q2(t0) 0 ... q'n(t0)$

Schreibe die $k$ -te Komponente obiger Gleichung auf:

qk(t) = qk(t0)+ (r(t0)) (t- t0)+ fk(t0)(t- t0) (fk ist stetig, fk(t0) = 0) k

qk(t) - qk(t0) tli'-->mt ----t--t----= (r'(t0))k 0 0

Definition:

Eine stetig differenzierbare Kurve $m r : I '--> R$ mit $' r (t) /= o,t (- I$ , heißt glatte (reguläre) Kurve. Ist $' r$ stückweise stetig, so heißt die Kurve $m r : I '--> R$ stückweise glatt. Eine Menge $K$ , die glatt ist, (Tangenten besitzt), kann eine Parameterdarstellungen besitzen, die nicht glatt sind.

Beispiele:

Glatte Kurve: $( ) t r(t) = t ,1 < t < 1$
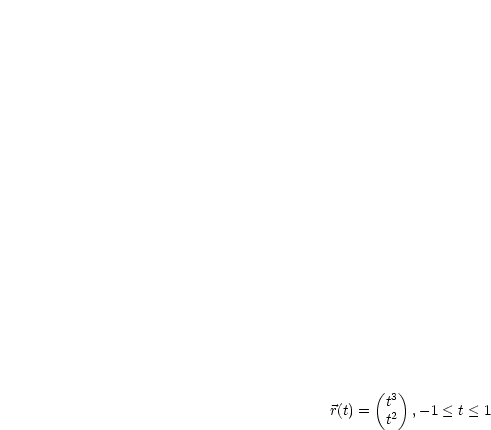
Nichtglatte Kurve: $(t3) r(t) = t2 ,- 1 < t < 1$

$( ) r'(0) = 0 0$

Definition:

Die Menge $K < Rm$ heißt glatt, falls es eine reguläre Parameterdarstellung gibt.

Satz:

$r = r(t),a < t < b$ sei $1 C$ -Kurve und regulär. Dann ist die Parametertransformation $t = g(t),a < t < b$ eine bijektive, stetig differenzierbare ( $r([a,b]) = r[(a,b)]$ ) Abbildung mit $' g(t) /= 0$ . $r(t) = r(g(t)),a < t < b$ unparametrisierte Kurve.

Beispiel:

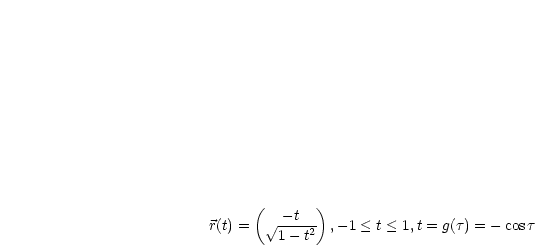
( ) V~ --t- r(t) = 1- t2 ,- 1 < t < 1,t = g(t) = - cost

( ) r(t) = cost ,0 < t < p sin t

' ' ' r (t) = r(g(t))g (t)

' ' ' ||r(t)||= ||r(g(t))|| .||g (t)||

Damit erhalten wir durch Differentiation folgenden Geschwindigkeitsvektor:

|--------------------| | r(t)- r(t0)| r'(t0) = tli'-->mt0--t--t---| -----------------0----

$||r'(t )|| 0$ ist der Betrag der Geschwindigkeit.

Orientierungserhaltende Parametertransformation: $' g (t) > 0 : g(a) = a,g(b) = b$
Orientierungsumkehrende Parametertransformation $' g (t) < 0 : g(a) = b,g(b) = a$

Beispiel:

t = r(t),a < t < b

r(t) = r(a+ b -t),a < t < b ---- ---- g(t)

3.2.1 Bogenlänge (Länge $L$ einer glatten Kurve $C$ )

Es sei $r = r(t)$ , $a < t < b$ , $r'(t) = o$ und $t (- [a,b]$ . Wir teilen die Kurve in Intervalle $a = t0 < t1 < t2 < ...< tk = b$ .

k sum -1 ||r(tj+1)- r(tj)|| j=0

Satz:

$r : [a,b] '--> Rm$ sei glatte Kurve im $Rm$ . Dann gilt für die Länge von $r([a,b])$ :

$integral b a ' L(C) = Lb(r) = ||r (t)||dt a$

Illustration:

l'(t) = Geschwindigkeit = ||r'(t)||

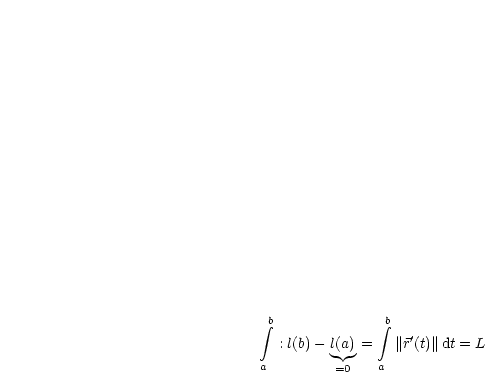
integral b integral b : l(b)- l(a)= ||r'(t)||dt = L a =0 a

Beispiel:

(cost) r(t) = e-t sint ,t > 0

Die Länge der Kurve berechnet sich durch folgendes Parameterintegral:

oo integral L(r) = ||r'(t)||dt 0

( ) ( ) ' -t cost - t sin t r (t) = - e sint + e cost

oo oo integral ' integral V~ -t V~ - L(r = ||r (t)||dt = 2e dt = 2 0 0

Beispiel:

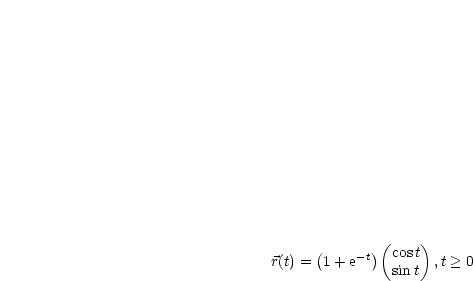
( ) ( -t) cost r(t) = 1 + e sin t ,t > 0

V~ --------------- ||r(t)||= e-2t + (1+ e-t)2 > 1+ e-t

oo integral oo integral L(r) = ||r'(t)|| dt > (1+ e-t)dt existiert nicht. 0 0

Beispiel:

( ) V~ --t- r(t) = 1- t2 ,- 1 < t < 1

' 2 --t2- --1-- ||r(t)|| = 1+ 1 - t2 = 1 - t2

integral +1 dt L(r) = V~ ---2-= p = arcsin| 1-1 -1 1 - t

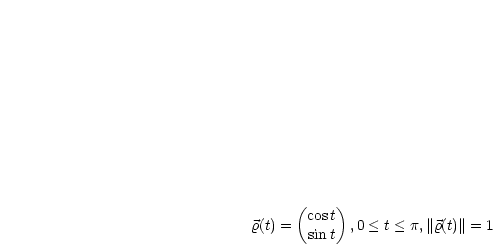
( ) cost r(t) = sint ,0 < t < p,||r(t)|| = 1

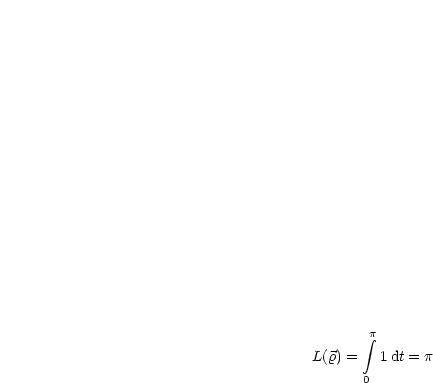
p integral L(r) = 1dt = p 0

Satz:

Der folgende Satz beschreibt die Invarianz der Bogenlänge gegen Parametertransformationen:

Es sei $r = r(t),a < t < b$ eine glatte Kurve und $g : [a,b] '--> [a,b](g = g(t))$ eine bijektive $C1$ -Funktion mit $g(t) /= 0$ . Bezeichnet $r(t) = r(g(t)),a < t < b$ die unparametrisierte Kurve, so gilt:

$integral b integral b L(r) = ||r'(t)||dt = ||r(t)||dt = L(r) a a$

Nachrechnen:

g'(t) < 0 : g(a) = b,g(b) = a,| g'(t)|= - g'(t)

b b b b a integral ' integral dr integral ' ' integral ' ' integral ' ||r(t)||dt = ||dt-g(t)||dt = ||r (g(t))||g(t)dt = - ||r(g(t))||g (t)dt = ||r (g(t))||g(t)dt a a a a b

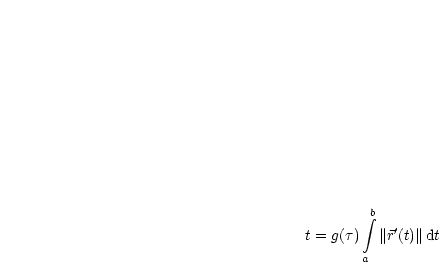
integral b t = g(t) ||r'(t)||dt a

Beispiel:

Wir betrachten die implizite Darstellung der Asteroide:

2 2 2 x3 + y3 = a3 mit a = const.

Die Kurve ist symmetrisch zur $x$ -Achse und $y$ -Achse. Infolgedessen brauchen wir nur $x > 0$ , $y > 0$ zu untersuchen.

( ) r(t) = acos3t ,0 < t < p asin3t 2

Wir berechnen die Länge der Kurve:

' 2 2 2 2 ||r (t)|| = 9a sin tcost

p integral 2 L = 4.3a. sintcostdt = 6a 0

3.2.2 Die natürliche Darstellung einer Kurve

$r = r(t),a < t < b$ sei glatte Kurve. $S$ ist der sogenannte Bogenlängenparameter. Mit $L$ wird die Länge der Kurve bezeichnet.

$integral t s = l(t) = ||r'(t)||dt,a < t < b a$

$l : [a,b] '--> [0,L]$ : Die Funktion ist bijektiv. $l'(t) = ||r'(t)|| > 0,$ sie ist also stetig differenzierbar. Das heißt: $s = l(t)$ ist als Parametertransformation brauchbar: $t = l'(s)$

$|--------------| | -1 | r(t) '--> -r(s)-=-r(l--(s))-$ , $0 < s < L$

Diese Darstellung heißt die natürliche Darstellung der Kurve/Darstellung bezüglich der Bogenlänge.

Wir bilden die Ableitung der Funktion:

' ' -1 -1' ' -1 ---1---- -r'(l--1(s))- ' 2 r(s) = r (l (s))(l )(s) = r(l (s)).l'(l-1(s)) = ||r'(l- 1(s))||:||r (s)|| = 1

integral s ls0(r) = ||r'(s)||ds = s 0

$r$ : $I '--> Rm$ sei glatte Kurve $r = r(t)$ . Sie ist bogenparametrisiert, falls $||r'(t)||= 1$ $A$ $t$ gilt.

Beispiel: Schraubenlinie

( ) cos t r(t) = sint ,0 < t < 2p t

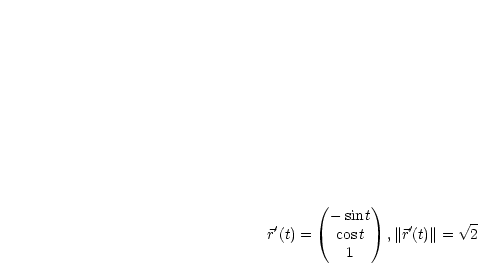
( ) - sin t V~ - r'(t) = cost ,||r'(t)||= 2 1

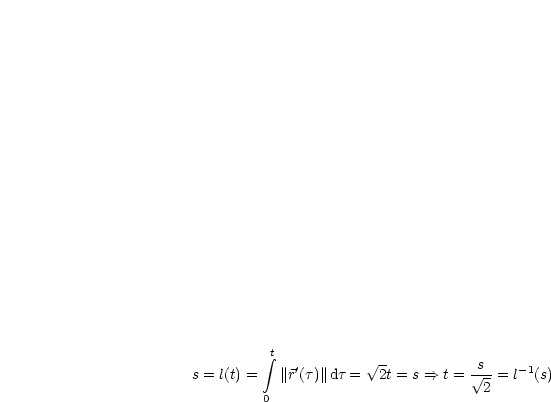
t integral ' V~ s -1 s = l(t) = ||r(t)||dt = 2t = s ==> t = V~ 2-= l (s) 0

Die natürliche Darstellung der Schraubenlinie lautet deshalb wie folgt:

(cos s V~ -) s2- V~ r(s) = sins V~ 2 ,0 < s < 2 2p V~ 2

Nun kann man die Länge zwischen zwei Werten schnell berechnen: $s Ls21(r) = s2 - s1$

Bemerkung:

$r = r(s)$ sei die natürliche Darstellung einer glatten Kurve. $1 = ||r'(s)|| 2 = r'(s)Tr'(s) D-i-ff-e-re-n-zi-e-re--> 0 = 2r'(s)r''(s)$ . $r''(s)$ ist eine Richtung, die senkrecht zur Kurve in Punkte $r = r(s)$ steht. $r''(s)$ ist der sogenannte Hauptnormalenvektor. Wer weiterhin noch Interesse hat, sollte die Begriffe Binormale und Fresnelsche Formel in einem Mathematikbuch nachschlagen.