

|
|
|
|
|
|
|
|
bei |
|
 . Wird
. Wird  bezüglich
von Basen in
bezüglich
von Basen in  durch eine Matrix dargestellt, so heißt diese Matrix
Ableitung von
durch eine Matrix dargestellt, so heißt diese Matrix
Ableitung von  in
in  , geschrieben
, geschrieben  .
.
Ist  differenzierbar in
differenzierbar in  , so gibt es eine
, so gibt es eine  -Matrix
-Matrix
 , wobei
, wobei  gilt.
gilt.
Ist  in
in  differenzierbar, so ist
differenzierbar, so ist  in
in  stetig.
stetig.

Diese Funktion ist in  nicht differenzierbar, da sie dort unstetig ist. (Obwohl
nicht differenzierbar, da sie dort unstetig ist. (Obwohl
 für alle
für alle  existiert.)
existiert.)
 sei eine konstante
sei eine konstante  -Matrix.
-Matrix.  ,
,  :
: 



|
Es sei |
|
|
Sei  gegeben. Setzen in die obige Definition
gegeben. Setzen in die obige Definition  (
( genügend
klein).
genügend
klein).
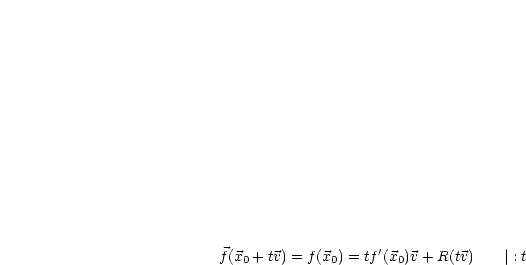
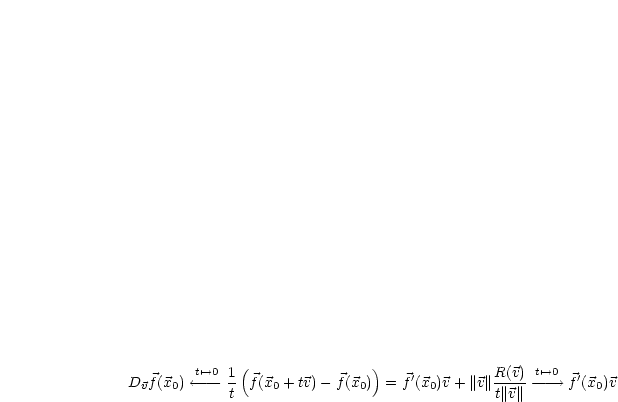
Es sei  in
in  differenzierbar. Setze in Satz 3
differenzierbar. Setze in Satz 3  für
für  ,
,  ,
,
 .
.
![[ ]
f'(x0)ej = Djf (x0) : f'(x0) = D1f (x0),D2f(x0),...,Dnf (x0) = Dp(x0)](ma2391x.gif)
 ist die
ist die  -te Spalte der Abbildungsmatrix. Setze in Satz 3:
-te Spalte der Abbildungsmatrix. Setze in Satz 3:


Setze  :
:

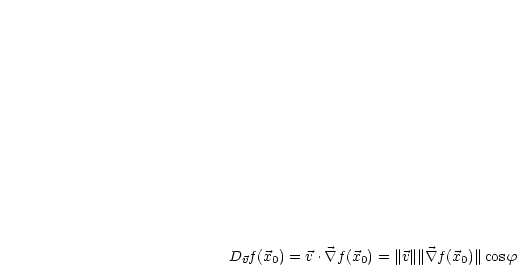


Für eine symmetrische Matrix  gilt:
gilt:



Es sei  ,
,  und
und  die explizite Darstellung (differenzierbar)
einer Fläche mit
die explizite Darstellung (differenzierbar)
einer Fläche mit  .
.
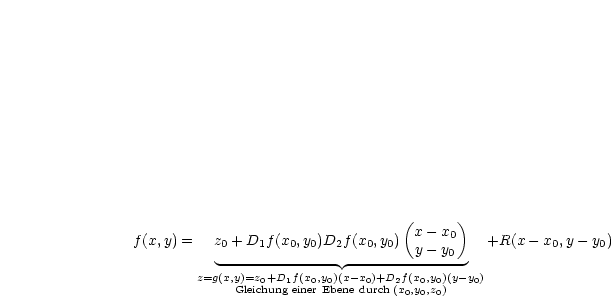
Dies ist eine Tangentialebene an die Fläche  in
in  . Der Normalenvektor
der Ebene lautet:
. Der Normalenvektor
der Ebene lautet:

Wir schauen uns folgende Menge an:




Bewegt man sich von  aus in Richtung
aus in Richtung  , so
bewegt man sich auf der Fläche auf der Linie des
, so
bewegt man sich auf der Fläche auf der Linie des  , der
sogenannten Fallinie.
, der
sogenannten Fallinie.



Zeige, daß  in (0,0) nicht differenzierbar, aber stetig ist.
in (0,0) nicht differenzierbar, aber stetig ist.
|
|
|
|
|
Falls alle |
|

Bei der Funktion  ist beispielsweise
ist beispielsweise  in
in  unstetig.
unstetig.
|
Es sei |
|
|
Es sei  ,
,  . Wir betrachten die Funktionen
. Wir betrachten die Funktionen  :
:  und
und  :
:
 .
.
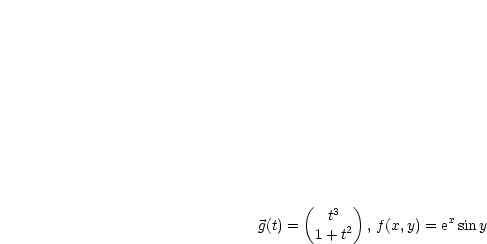
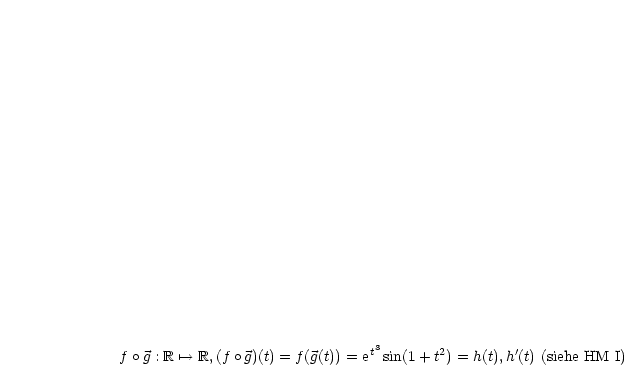




Es sei  :
:  und
und  :
:  .
.

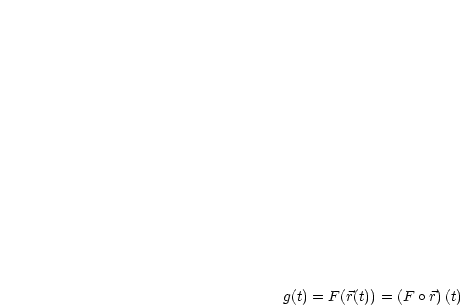
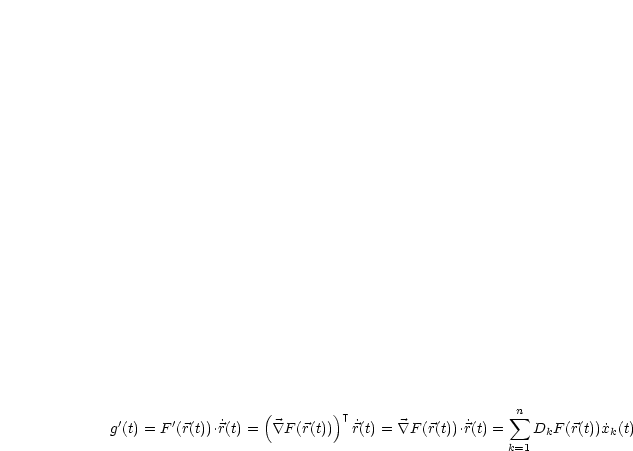
Für den Fall  ist
ist  die implizite Darstellung einer Fläche.
Durch
die implizite Darstellung einer Fläche.
Durch  wird beispielsweise eine Ebene dargestellt und
wird beispielsweise eine Ebene dargestellt und
 ist eine Kugel um
ist eine Kugel um  mit Radius
mit Radius  .
.



 ist die Tangentenrichtung an
ist die Tangentenrichtung an  in
in  .
.
 ist der Normalenvektor von
ist der Normalenvektor von  in dem Punkt
in dem Punkt  , der durch
, der durch  gegeben ist.
gegeben ist.
|
Es sei |
Dann ist 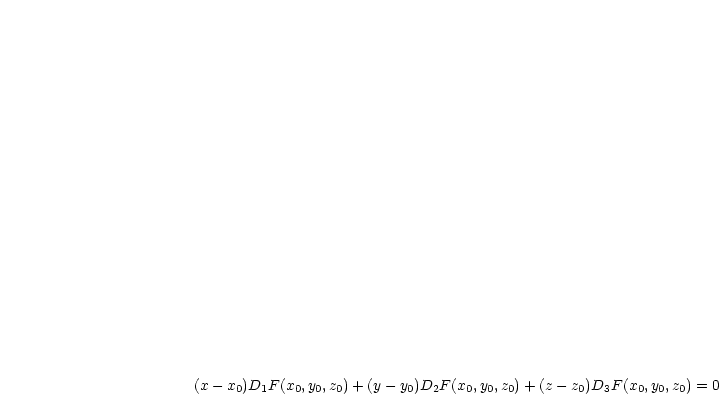
|



 in
in 


Eine Kugel um den Ursprung mit Radius 1 wird beschrieben durch:
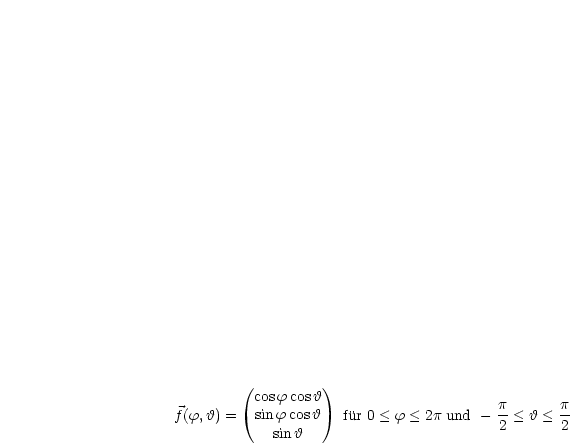




˙r1(0) = f'(u0,v0) 1 D1f(u0,v0),D2f (u0,v0) 1 = D1f (u0,v0)
0 0](ma2503x.gif)

Die Parameterdarstellung für die Tangentialebene lautet:
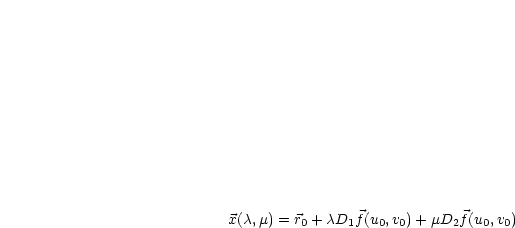
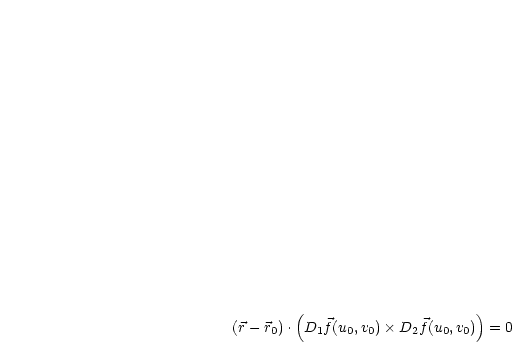



|
|
|

 stetig differenzierbar stetig differenzierbar 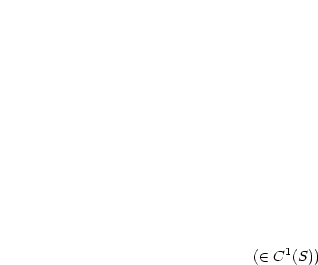 , so ist , so ist  differenzierbar. differenzierbar. |
Es seien  und
und  wie zuvor definiert.
wie zuvor definiert.  bezeichnet man als
Niveaumenge von
bezeichnet man als
Niveaumenge von  . Es gilt
. Es gilt 

 für
für  . Niveaumengen heißen
für
. Niveaumengen heißen
für  Höhenlinien und für
Höhenlinien und für  ÄQUIPOTENTIALFLÄCHEN.
ÄQUIPOTENTIALFLÄCHEN.

 mit der Wärmeleitfähigkeit
mit der Wärmeleitfähigkeit

 |
|
Ein Vektorfeld |
|
|
Für ein |
|
Gegeben sei  . Ist
. Ist  ein Potentialfeld?
ein Potentialfeld?
Falls  ein Potentialfeld ist, folgt
ein Potentialfeld ist, folgt  ,
,  und
und 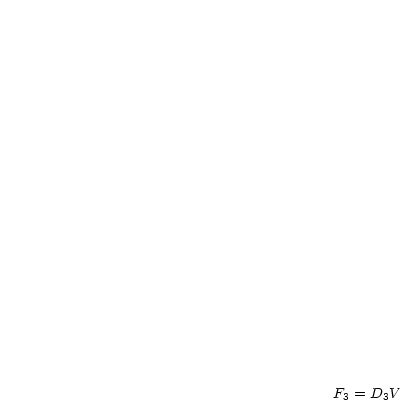 .
.

Die Äquipotentialflächen sind nichts anderes als Kugelflächen:


Die Kraft steht senkrecht auf den Äquipotentialflächen (Kugelflächen).

 ist auf
ist auf  ,
,  definiert und
stetig.
definiert und
stetig.  existiere und sei stetig auf
existiere und sei stetig auf  . Daraus folgt (ohne
Beweis):
. Daraus folgt (ohne
Beweis):
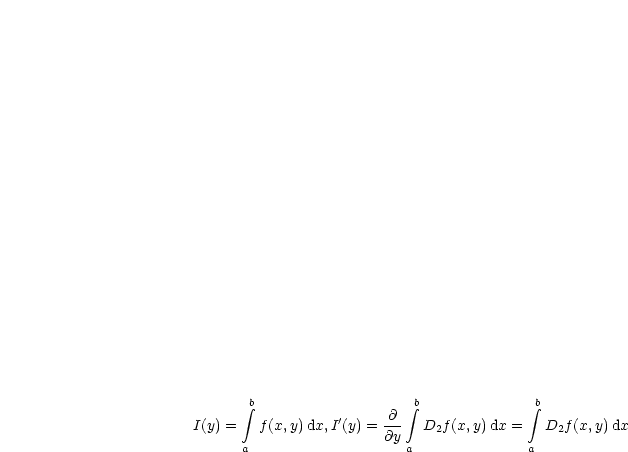
 ,
,  :
: ![[c,d] '--> [a,b]](ma2565x.gif) sei differenzierbar. Es gilt:
sei differenzierbar. Es gilt:

![x integral 2
G(x1,x2,x3) := f(x1,x3)dx wobei G : [a,b]×-[a,b]×-[c,d]'--> R
x1 ---------R3----------
F(y)=G(g(y))](ma2567x.gif)
![(p(y))
g(y) = q(y) wobei g : [c,d] '--> R3
y](ma2568x.gif)
 | (3.4) |