3.6 Taylorformel

[next] [prev] [prev-tail] [tail] [up]

3.6 TAYLORformel

Definition:

$n S < R$ heißt konvex, falls für alle Punkte $n a,b (- R$ gilt: ${a+ t(b- a),0 < t < 1} < S$ .
TAYLORformel (HM I):
$F : [0,1] '--> R$ sei $k$ -mal stetig differenzierbar und $(k+1) F$ existiere auf $(0,1)$ . Dann gibt es ein $h (- (0,1)$ mit folgender Eigenschaft:
$sum k 1 1 F(1) = j!F (j)(0)+ (k-+-1)!F (k+1)(h) = j=0-- ---- ------ ------ Tk Rk$
$1 1 1 = F (0)+ F '(0)+ 2!F ''(0)+ 3!F '''(0)+ ...+ (k-+-1)!F (k+1)(h)$
$n S (_ R$ offen, konvex; $n k f : S (_ R '--> R,f (- C (S),f$ sei $(k+ 1)$ -mal partiell differenzierbar. ( $x,x0 (- S;h = x- x0)$

Wende $zk$ auf $F (t) = f(x0 + th)$ ( $0 < t < 1$ ) an:

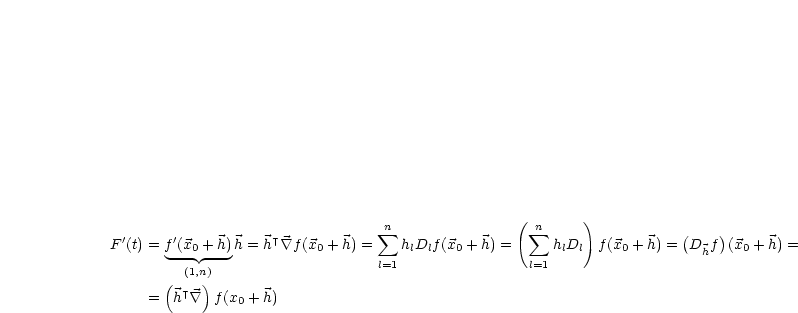( ) ' ' T sum n sum n ( ) F (t) = f(x0 +-h)h = h \~/ f (x0 + h) = hlDlf(x0 + h) = hlDl f(x0 + h) = Dhf (x0 + h) = (1,n) l=1 l=1 ( T ) = h \~/ f(x0 + h)

(3.5)

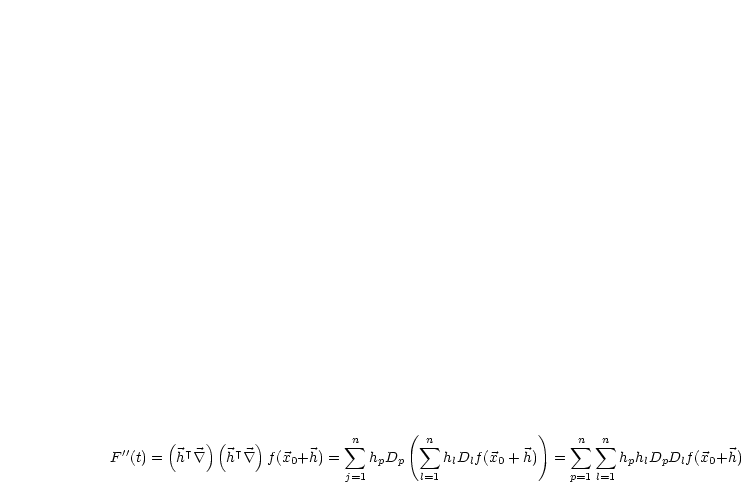
( )( ) sum n ( sum n ) sum n sum n F''(t) = hT \~/ hT \~/ f (x0+h) = hpDp hlDlf(x0 +h) = hphlDpDlf (x0+h) j=1 l=1 p=1 l=1

sum n sum n sum n ( )j F(j)(t) = ... hljhlj- 1 ...hl1Dlj ...Dl1f(x0+h) = hT \~/ f(x0+h) lj=1 l2=1l1=1

TAYLORsatz:

Für alle $x,x0 (- S$ gilt: Es gibt ein $h (- (0,1)$ mit:

$sum k ( )j ( )k+1 f(x) = 1- (x- x0)T \~/ f (x0)+ ---1--- (x - x0)T \~/ f(x0 + h(x - x0)) j=0 j! (k-+1)!----------- ----------------- ---------- ---------- Rest (||x-x0|| k),x'-->x0 Tk TAYLORpolynom von Grad k$

Spezialfälle:

Den Fall $n = 1$ haben wir schon in HM I abgehandelt:

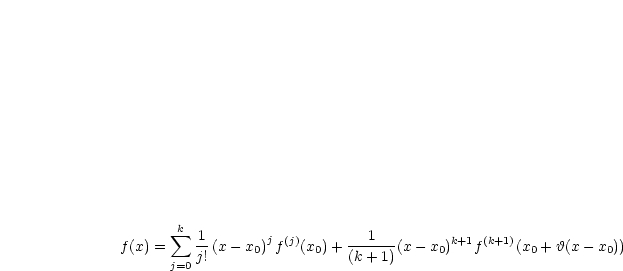
sum k 1- j (j) --1--- k+1 (k+1) f(x) = j! (x - x0)f (x0)+ (k + 1)(x - x0) f (x0 + h(x - x0)) j=0

Für $k = 0$ folgt der Mittelwertsatz der Differentialrechnung:

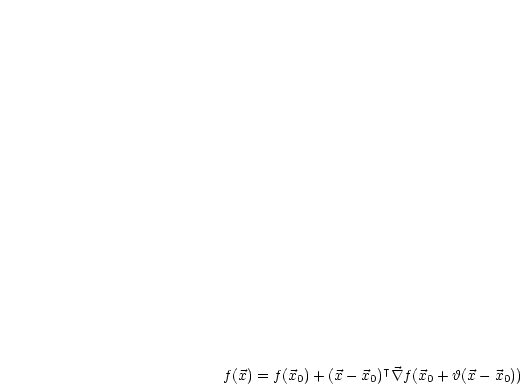
T f(x) = f(x0)+ (x- x0) \~/ f (x0 + h(x - x0))

Für $n = 2$ lautet der Mittelwertsatz:

x = (x,y),x0 = (x- 0,y0)

f(x,y) = f(x0,y0) = (x- x0)D1f(x0+h(x- x0)y0+h(y -y0))+(y -y0)D2f(x0+h(x- x0)y0+h(y -y0))

Folgerung:

$n f : S (_ R '--> R$ sei stetig differenzierbar. Dann gilt: $f = const$ in $S$ $<==>$ $\~/ f (x) = o$ für $x (- S$

Mit Mittelwertsatz folgt: Wähle $x0$ , $x1 (- S$ : $f(x0)- f(x1) = (x0- x1)T \~/ f (x0 + h(x1 - x0)) = 0$

Beispiel:

S = {(x,y)| x > 0,y > 0}

x y f(x,y) = arctan-+ arctan -- y x

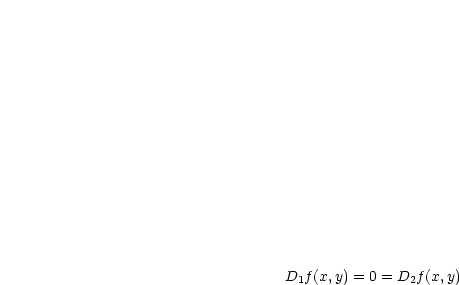
D1f(x,y) = 0 = D2f(x,y)

==> \~/ f(x,y) = o A (x,y) (- S

==> f(x,y) = const. = f(1,1) = 2arctan1 = p 2

Entwicklung bis zur Ordnung $k = 2$ :

( 0 0 0 )2 sum n 0 0 (x1 - x1)D1 + (x2- x2)D2 + ...+ (xn- xn)Dn f(x0) = (xj- xj)(xk- xk)(DjDkf-(x0)) j,k=1 Hf(x0)

H (x ) = (D D f(x )) f 0 j k 0 j=1,2,...,n

Dies ist gerade die sogenannte HESSEsche Matrix (symmetrisch).

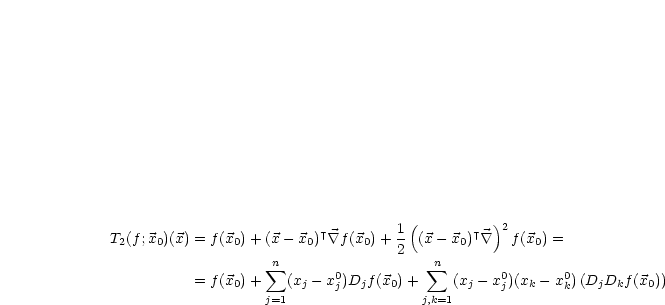( ) T2(f ;x0)(x) = f(x0)+ (x- x0)T \~/ f (x0) + 1 (x -x0)T \~/ 2f(x0) = 2 sum n 0 sum n 0 0 = f(x0)+ (xj- xj)Djf(x0)+ (xj - xj)(xk -xk)(DjDkf (x0)) j=1 j,k=1

(3.6)

Betrachten wir als Beispiel die Hesse-Matrix für $n = 2$ :

( D21f D1D2f ) Hf(x0,y0) = D2D1f D22f (x0,y0)

Übung:

Berechne $T3(f;x0)(x)$ !

Beispiel:

$f(x,y) = (x - 1)4(y- 2)3$ soll um $(0,0)$ bis zur 1.Ordnung entwickelt werden.

|-------------| f(x,y) ~~ T1(f(0,0))(x,y) = f(0,0)+-(x--0)D1f(0,0)+-(y--0)D2f(0,0)=--8-+32x-+-12y t(x,y)

Dies ist Gerade die Gleichung der Tangentialebene an die Fläche durch den Punkt (0,0).

Beispiel:

f(x,y) = ex+y + sin(xy)

Entwickle um (0,0) bis zur 3.Ordnung:

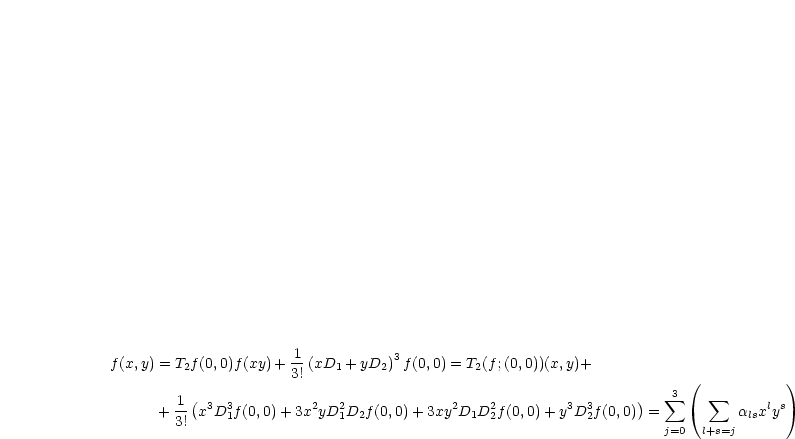f(x,y) = T2f(0,0)f(xy)+-1 (xD1 + yD2)3f (0,0) = T2(f;(0,0))(x,y)+ 3! ( ) 1 ( 3 3 2 2 2 2 3 3 ) sum 3 sum l s + 3! x D1f(0,0)+ 3x yD1D2f (0,0) +3xy D1D 2f(0,0)+ y D2f(0,0) = alsx y j=0 l+s=j

(3.7)

Wir nehmen zur Berechnung der TAYLORreihe die uns schon bekannte Reihe der Exponentialfunktion und der Sinusfunktion:

oo sum sum oo k |----------------------------------| f(x,y) = 1-(x+y)j+ --(--1)--(xy)2k+1 = 1 + x+ y + 1(x+ y)2 + 1-(x+ y)3 + ... j=0j! k=0(2k + 1)! -----------2---------3!-------------

Beispiel:

$2 2 f(x,y) = x - y$ um (0,0) entwickeln bis zur 4.Ordnung:

2 2 f(x,y) = x - y!

Entwickle um (1,2):

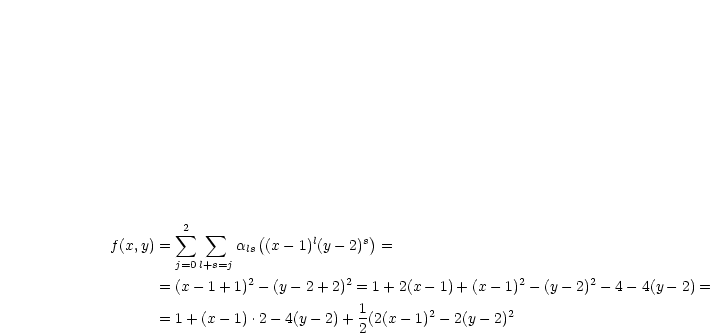sum 2 sum ( l s) f(x,y) = als (x- 1) (y - 2) = j=0l+s=j = (x- 1+ 1)2- (y- 2 + 2)2 = 1+ 2(x- 1)+ (x- 1)2- (y- 2)2- 4- 4(y- 2) = 1 2 2 = 1+ (x- 1).2 - 4(y - 2)+ 2(2(x- 1) - 2(y- 2)

(3.8)

Beispiel:

Wir entwickeln die Funktion $f$ um $x = (1,-1,0) 0$ bis zur 2.Ordnung:

|----------------z--------2| f-(x,y,z) =-(x--1)e---(y+-1)-

Zuerst berechnen wir die ersten und zweiten partiellen Ableitungen:


$z fx = e$	$fy = -2(y +1)$	$z fz = (x - 1)e$


$fxx = 0$	$fyx = 0$	$z fzx = e$
$fxy = 0$	$fyy = - 2$	$fzy = 0$
$z fxz = e$	$fyz = 0$	$z fzz = (x - 1)e$

\text{[math]}

Damit gilt also:

1 T0(x,y,z) =--f(1,-1,0) = 1 .0 = 0 0!

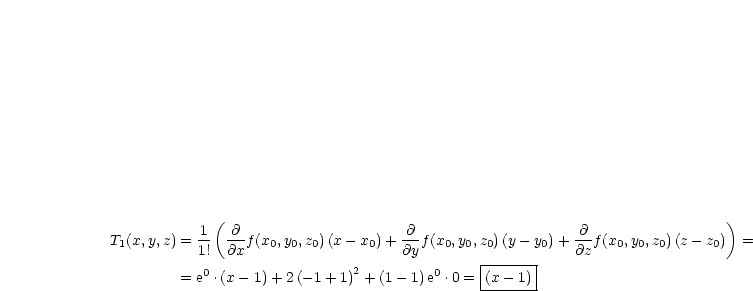( ) T (x,y,z) = 1- -@-f(x ,y,z )(x- x )+ -@-f(x ,y ,z )(y- y )+ @-f(x ,y ,z)(z- z ) = 1 1! @x 0 0 0 0 @y 0 0 0 0 @z 0 0 0 0 = e0 .(x - 1)+ 2(-1 + 1)2 +(1 -1)e0 .0 =|(x---1)| --------

(3.9)

1-(-@2- 2 -@2-- --@2- -@2-- T2(x,y,z) = 2! @x2 (x- x0) + @x@y (x- x0)(y- y0)+ @x@z (x -x0)(z -z0)+ @x@y (x - x0) (y - y0)+ 2 2 2 +-@-2 (y- y0)2 +-@--(y - y0)(z - z0) + -@---(z - z0)(x - x0) + @y @y@z ) @z@x +--@2-(z- z )(y- y )+ -@2 (z - z)2 @z@y 0 0 @z2 0

(3.10)

Durch Einsetzen der Zahlenwerte folgt:

1( 2 ) 2 T2(x,y,z) = 2 0 + 0+ 1.(x -1)z + 0- 2.(y +1) + 0 + 1.z(x- 1)+ 0 + 0 = (x -1)z- (y+ 1)

Damit gilt also:

------------------------------------ | 2| -f(x,y,z) ~~ -(x---1)+-(x---1)z--(y+-1)-

Beispiel:

Es soll folgende Funktion um $P (1,- 1,0)$ bis zur 2.Ordnung entwickelt werden:

|-----------------| f(x,y,z) = xez- y2| -------------------

Für die partiellen Ableitungen gilt:


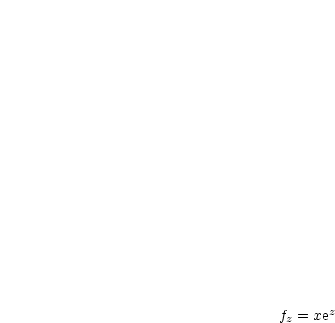$z fx = e$	$fy = -2y$	$z fz = xe$


$fxx = 0$	$fyx = 0$	$z fzx = e$
$fxy = 0$	$fyy = - 2$	$fzy = 0$
$z fxz = e$	$fyz = 0$	$z fzz = xe$

\text{[math]}

Damit gilt also:

0 2 T0 = 1.e - (-1) = 0

T1 = 1 .(x - 1)+ 2(y+ 1)+ z = 1+ x+ z + 2y

1 ( ) T2 = -. 0 + 0+ 1.(x- 1)z + 0- 2(y+ 1)2 + 0+ 1 .(x - 1)z + 0 +z2 = 21 1 1 1 = -(x- 1)z - (y + 1)2 + -(x- 1)z + -z2 = (x - 1)z- (y+ 1)2 +-z2 2 2 2 2

(3.11)

Also folgt:

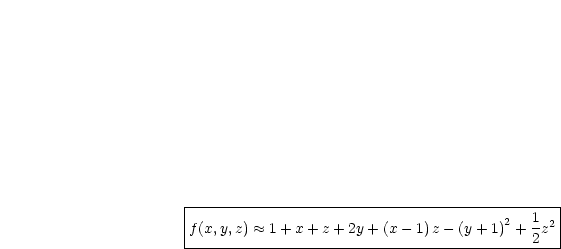
|----------------------------------------------| | 2 1 2| |f(x,y,z) ~~ 1+ x+ z + 2y+ (x- 1)z- (y +1) + 2z | ------------------------------------------------

Beispiel:

Wir entwickeln folgende Funktion um den Punkt $P(0,0)$ bis zur dritten Ordnung:

|-----------(------)-| f (x) = arctan x---y- | --------------1+-xy---

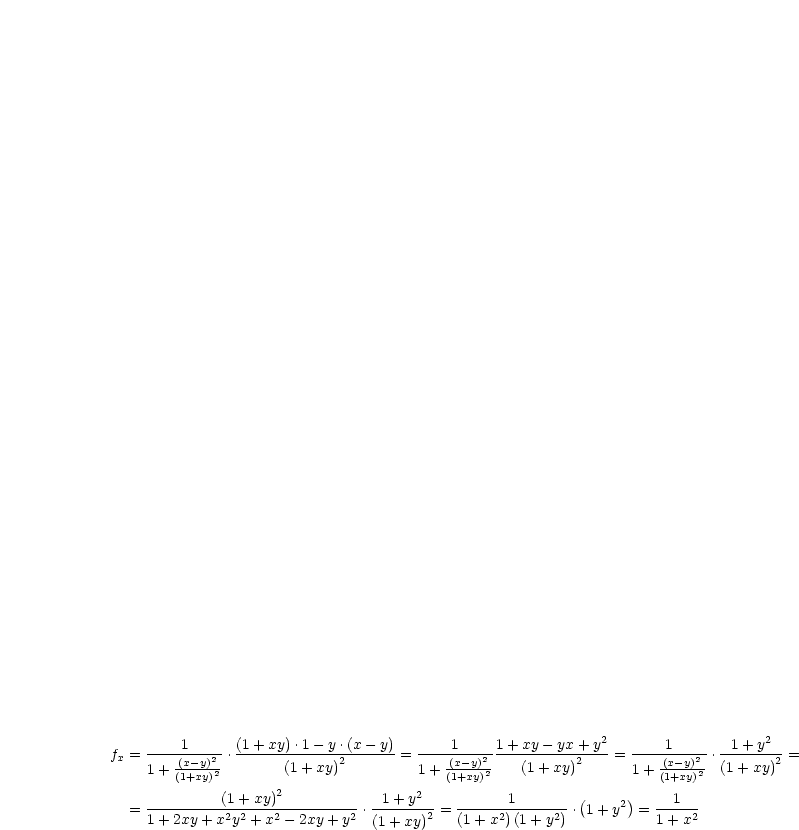-----1---- (1-+-xy).1--y.(x---y) -----1----1+-xy---yx+-y2 ----1----- -1-+-y2- fx = 1 + (x-y)22 . (1 + xy)2 = 1 + (x-y)22 (1+ xy)2 = 1+ (x--y)22-.(1+ xy)2 = (1+xy) (1+xy) (1+xy) ----------(1-+-xy)2--------- -1+-y2-- -------1------ ( 2) --1--- = 1 + 2xy+ x2y2 + x2 -2xy + y2 . (1 + xy)2 = (1+ x2)(1+ y2) .1 + y = 1 +x2

(3.12)

Analog folgt:

fy = ---1--- 1+ y2

Wir berechnen die zweiten Ableitungen:

-2x gxx = (1-+-x2)2

g = g = 0 yx xy

---2y--- gyy = (1 + y2)2

Für die dritten partiellen Ableitungen gilt:

g = g = g = g = 0 xxy yxx xyy yyx

(1+ x2)2 .(-2)+ 2x .2.(1+ x2).2x - 2- 2x2 + 8x2 6x2- 2 gxxx = -----------------23-------------= --------2-3-- = -----2-3 (1 + x ) (1+ x ) (1+ x )

2 gyyy = -2--6y-- (1+ y2)3

Man erhält dann:

T0 = 1.arctan(0) = 0

T1 = 1.(gx(0,0).x + gy(0,0).y) = x- y

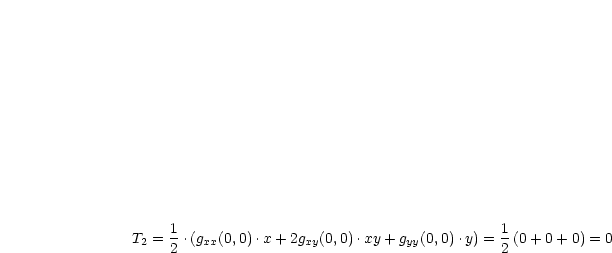
T2 = 1 .(gxx(0,0).x+ 2gxy(0,0) .xy+ gyy(0,0).y) = 1(0+ 0 + 0) = 0 2 2

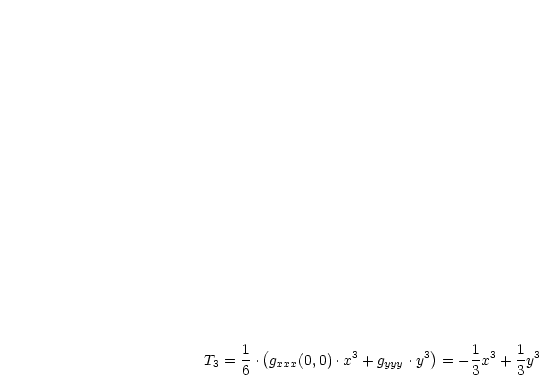
1 ( ) 1 1 T3 =- . gxxx(0,0).x3 + gyyy .y3 = --x3 +-y3 6 3 3

Also folgt schlußendlich:

|----------------------| | 1 3 1 3| -f(x) ~~ -x--y---3x-+-3y--

[next] [prev] [prev-tail] [front] [up]