|
|
Gilt „ |
|
|
|
Gilt „ |
|

Das Minimum liegt bei  ; ein Maximum gibt es nicht.
; ein Maximum gibt es nicht.
|
|
|
Es ist  :
: ![[- e,e] '--> R](ma2703x.gif) . Bei
. Bei  liege Maximum. Oder mit anderen Worten:
liege Maximum. Oder mit anderen Worten:
 hat bei
hat bei  ein Maximum.
ein Maximum.

 mit mit 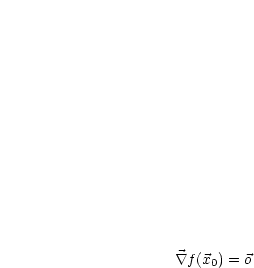 heißt stationärer Punkt von heißt stationärer Punkt von  . . |
Ist  in der Menge
in der Menge  differenzierbar, so sind die Punkte, in denen
differenzierbar, so sind die Punkte, in denen  extremal
wird, unter den stationären Punkten zu suchen.
extremal
wird, unter den stationären Punkten zu suchen.

Wir bilden den Gradienten:

Hieraus ergibt sich, daß  der einzige stationäre Punkt ist. In jeder Umgebung
von (0,0) ist
der einzige stationäre Punkt ist. In jeder Umgebung
von (0,0) ist  positiv und auch negativ. Bei (0,0) kann folglich weder ein Maximum
von ein Minimum liegen.
positiv und auch negativ. Bei (0,0) kann folglich weder ein Maximum
von ein Minimum liegen.
|
|
|
|
|
 heißt positiv definit:
heißt positiv definit: 


 heißt negativ definit:
heißt negativ definit: 


 heißt indefinit:
heißt indefinit:  ,
, 

Für  ,
,  ,
,  wenden wir den TAYLORsatz an:
wenden wir den TAYLORsatz an:

 ist minimal.
ist minimal.
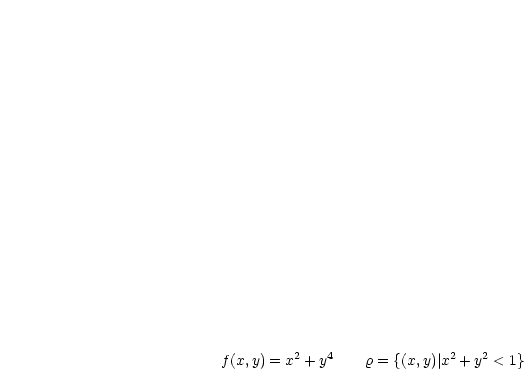

 ist stationär sowohl für
ist stationär sowohl für  als auch für
als auch für  . Die HESSEmatrix
. Die HESSEmatrix
 ist positiv semidefinit.
ist positiv semidefinit.
Da 

 , ist
, ist  ist eigentliches Minimum.
ist eigentliches Minimum.  hat in (0,0)
jedoch einen Sattelpunkt:
hat in (0,0)
jedoch einen Sattelpunkt:  .
.

Für  gilt
gilt  und
und  . Dies kann man
immer als eine Fläche im
. Dies kann man
immer als eine Fläche im  deuten.
deuten.



Die HESSEmatrix lautet  ; diese ist symmetrisch. Im
Falle
; diese ist symmetrisch. Im
Falle  gilt:
gilt:


 :
:
Semidefinitheit liegt für  vor.
vor.


Es sei  : Wir betrachten die Funktion
: Wir betrachten die Funktion  .
Gesucht sind lokale Extremwerte dieser Funktion.
.
Gesucht sind lokale Extremwerte dieser Funktion.
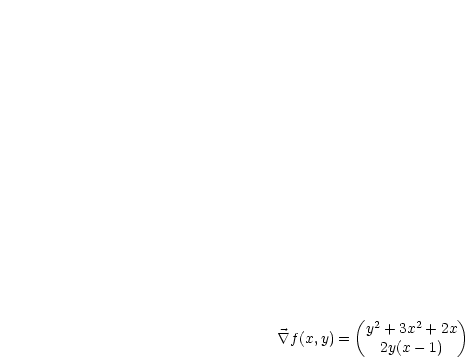
Die stationären Punkte bekommt man nun durch Nullsetzen:


Aus der zweiten Gleichung ergibt sich  oder
oder  .
.
 in erste Gleichung:
in erste Gleichung:

 und
und  sind stationäre Punkte.
sind stationäre Punkte.
 in erste Gleichung:
in erste Gleichung:

Diese Gleichung ist in  nicht lösbar.
nicht lösbar.  ,
,  sind
alle stationäre Punkte.
sind
alle stationäre Punkte.


Hier liegt Indefinitheit vor; bei (0,0) haben wir folglich einen Sattelpunkt.
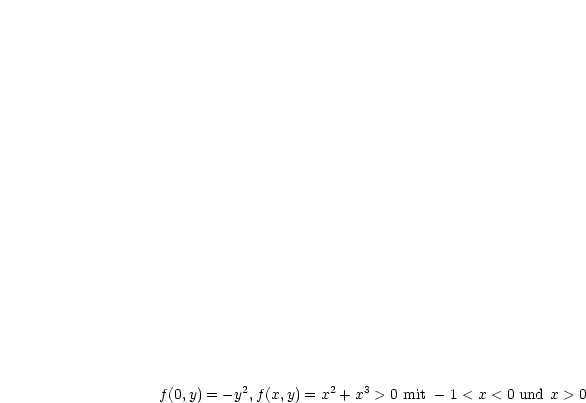

Hier liegt wegen negativer Definitheit ein lokales Maximum vor.

Als Übung kann überprüft werden, ob Randmaxima oder -minima vorliegen.
|
|
|
In HM I hatten wir: Falls ![f : [a,b] '--> R](ma2818x.gif) stetig ist, besitzt es gleichzeitig ein
Maximum und Minimum.
stetig ist, besitzt es gleichzeitig ein
Maximum und Minimum.
|
|
Betrachten wir das Problem für  : Gesucht sind Extremwerte von
: Gesucht sind Extremwerte von

 . Untersuche wie im
vorhergehenden Abschnitt.
. Untersuche wie im
vorhergehenden Abschnitt.
 nicht differenzierbar ist
nicht differenzierbar ist 
 auf
auf  (Parameterdarstellung des Randes suchen und in
Funktion einsetzen)
(Parameterdarstellung des Randes suchen und in
Funktion einsetzen)



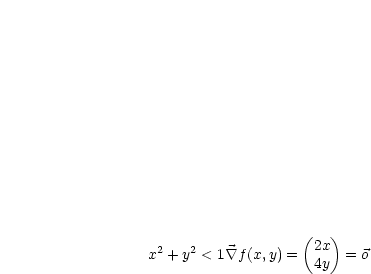
 ist somit der einzige stationäre Punkt; es handelt sich um ein
isoliertes globales Minimum (siehe HESSEmatrix).
ist somit der einzige stationäre Punkt; es handelt sich um ein
isoliertes globales Minimum (siehe HESSEmatrix).
 auf
auf  untersuchen
untersuchen 
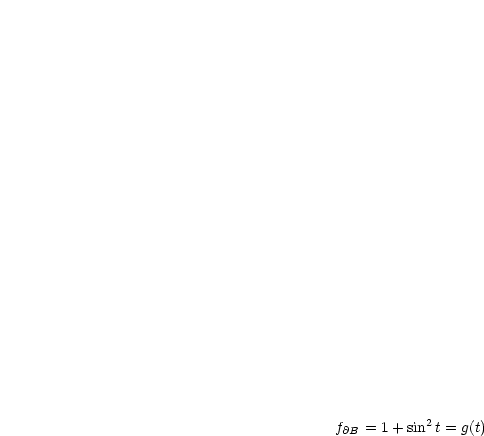
Wegen der Symmetrie von  und
und  genügt es,
genügt es,  für
für  ,
,  zu untersuchen.
zu untersuchen.


 :
:  ,
,  sind mögliche
Maximumpunkte für
sind mögliche
Maximumpunkte für  .
.
 :
:  ,
,  sind mögliche
Minimumpunkte für
sind mögliche
Minimumpunkte für  .
.
Frage: Wird  in
in  lokal maximal? Wir untersuchen
lokal maximal? Wir untersuchen  nahe
nahe
 :
:

Hier liegt somit ein lokales Maximum vor.
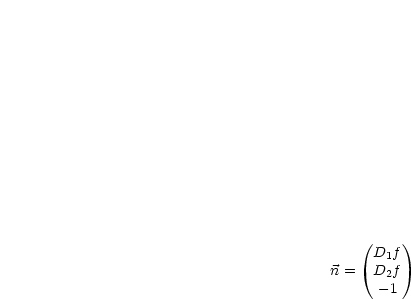
Daraus ergibt sich, daß  nach außen gerichtet sein muß.
nach außen gerichtet sein muß.  : Wir
schneiden die Fläche mit der
: Wir
schneiden die Fläche mit der  -
- -Fläche. Falls es sich um ein Minimum handelt, so
muß
-Fläche. Falls es sich um ein Minimum handelt, so
muß  ins Innere von
ins Innere von  gerichtet sein.
gerichtet sein.  geht nach außen;
es liegt daher kein Minimum für
geht nach außen;
es liegt daher kein Minimum für  vor.
vor.

Es liegt daher kein Minimum vor.
|
|
|
Die glatte Kurve |
|
|
|
Ist |
|