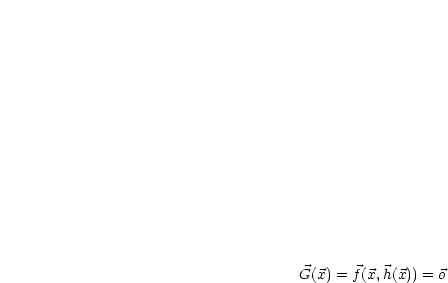|
|
Problem: |
|
|
|
Problem: |
|
 :
:


|
|




Satz 1 besagt: Zu  gibt es eine Umgebung
gibt es eine Umgebung  , die umkehrbar stetig
differenzierbar auf eine Umgebung von
, die umkehrbar stetig
differenzierbar auf eine Umgebung von  abgebildet wird. Diese
Abbildung ist sogar global (auf ganz
abgebildet wird. Diese
Abbildung ist sogar global (auf ganz  umkehrbar stetig differenzierbar):
umkehrbar stetig differenzierbar):

Daß  global umkehrbar ist, folgt nicht aus
global umkehrbar ist, folgt nicht aus 
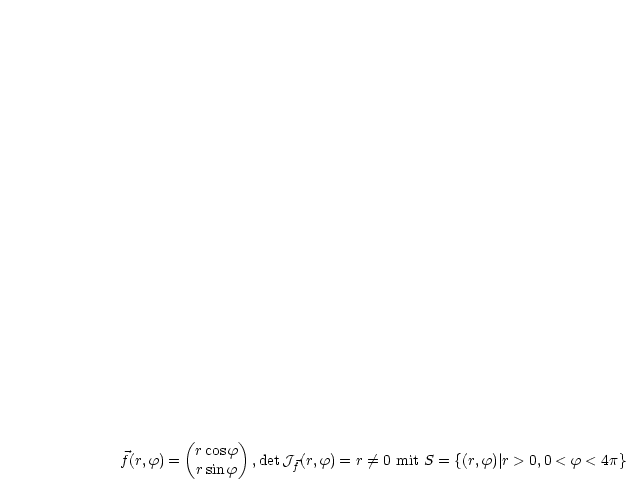
 ist auf
ist auf  nicht global injektiv.
nicht global injektiv.


Gesucht ist  ,
,  ; wir müssen dazu
; wir müssen dazu  ,
,  auflösen:
auflösen:

Infolgedessen ist diese Funktion  nach Satz 1 in der Umgebung von jedem
nach Satz 1 in der Umgebung von jedem
 stetig differenzierbar umkehrbar.
stetig differenzierbar umkehrbar.  ist jedoch nicht global invertierbar.
Die Abbildung hat folgende Eigenschaften:
ist jedoch nicht global invertierbar.
Die Abbildung hat folgende Eigenschaften:

Dadurch ist die Injektivität verletzt, die Funktion ist nicht global umkehrbar.
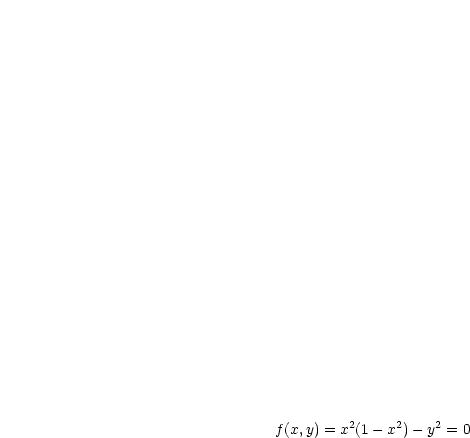
Ist die Gleichung  nach
nach  auflösbar
auflösbar  oder nach
oder nach
 auflösbar
auflösbar  , so werden
, so werden  und
und  implizit durch
implizit durch  definiert.
definiert.

Mit der Ungleichung zwischen geometrischem und arithmetischem Mittel gilt:

Für  wird
wird  .
.


Die Gleichung  besitzt in der Umgebung eines Punktes
besitzt in der Umgebung eines Punktes
 mit
mit  eine Auflösung
eine Auflösung  (
( , falls
, falls
 .
.


Aus  mit
mit  ,
,  (
( ) ergeben sich
) ergeben sich  Gleichungen
mit
Gleichungen
mit  Unbekannten. Setze
Unbekannten. Setze  mit
mit  ,
,  und
und  .
.
 soll nach
soll nach  aufgelöst werden: Man erhält
aufgelöst werden: Man erhält  Gleichungen mit
Gleichungen mit  Unbekannten.
Unbekannten.
![f'(x,y)= [D f (x,y),D f(x,y),...,D f(x,y),D f(x,y),...,D f(x,y)]
-- -- -1-------2--- --------n---- -m1-------- --m+n------
(m,m+n) (m,n) (m,m)](ma2977x.gif)
|
Dann gelten:
|
 sei eine
sei eine  -Matrix. Wir betrachten:
-Matrix. Wir betrachten:


![f(x,y) = A x + A y = o A = [A ,A ]
1 2 1 2](ma2996x.gif)

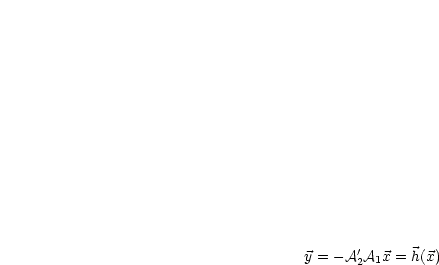
Für  und
und  gilt:
gilt:


Wir wollen nach  ,
,  auflösen:
auflösen:


Dann ist die Ableitungsmatrix an der geforderten Stelle regulär:

Aus dem Satz folgt: