3.9 Extremwertaufgaben mit Nebenbedingungen (NB)

Beispiel:

Es ist $f(x,y,z) = xyz$ zu minimieren, wobei $f$ : $R3 '--> R$ .

y1(x,y,z) = 0

y2(x,y,z) = 0

Außerdem gelten die folgenden Nebenbedingungen:

x + y+ z -5 = 0

yz + zx + xy- 8 = 0

Beispiel:

Gesucht sind die Punkte $P1(x,y)$ des Kreises $2 2 {(x,y)| x + y = 1}$ und die Punkte $Q = (u,v)$ der Geraden ${(u,v)| u + v = 4}$ , die voneinander minimalen Abstand haben. Es ist $2 2 f(x,y,u,v) = (x- u) + (y- v)$ zu minimieren unter den Nebenbedingungen $2 2 x + y - 1 = 0$ und $u + v- 4 = 0$ .

Problem:

Es ist $f$ : $Rn '--> R$ zu minimieren. Die Nebenbedingungen sind $g1(x,y,z) = 0$ und $g2(x,y,z) = 0$ . $C = F1 /\ F2$ ist eine Kurve. ( $\~/ g1$ , $\~/ g2$ sind linear unabhängig.) Gesucht ist nun ${f(x,y,z)| )x,y,z) (- C}$ . Es sei $r = r(t)$ , $t (- I$ eine Parameterdarstellung von $C$ . Es ist $F (t) = f(r(t))$ zu minimieren für $t (- I$ . Wird $F$ in $t (- I 0$ minimal, so gilt:

r'(t) = \~/ f (r(t0))Tr'(t0) = \~/ f (r(t0)) .r'(t0) = 0

Wird $F$ in $P$ minimal, so gilt $\~/ f (x0,y0,z0)$ $_L$ $C$ . Da $C < F1$ ist, wissen wir auch, daß $\~/ g(x0,y0,z0)$ $_L$ $C$ und $\~/ g2(x0,y0,z0)$ $_L$ $C$ gilt. Hieraus folgt, daß $\~/ f$ , $\~/ g1$ und $\~/ g2(x0,y0,z0)$ in der Ebene durch $P$ mit $n = r'(t0)$ liegen.

Sie sind linear abh¨angig-- \~/ -g--, \~/ -g -l-in-e-ar--un-a-b-h-an-g-->ig \~/ f (x0,y0,z0) = c1 \~/ g1(x0,y0,z0)+ c2 \~/ g2(x0,y0,z0) 1 2 ¨

$(x ,y ,z ) 0 0 0$ , $c 1$ , $c 2$ lassen sich bestimmen aus den Gleichungen:

\~/ f (x0,y0,z0) = c1 \~/ g(x0,y0,z0)+ c2 \~/ g2(x0,y0,z0)

g1(x0,y0,z0) = g2(x0,y0,z0) = 0

Satz (Lagrange-Multiplikatorenregel):

Gegeben sind $f$ : $S (- Rn '--> R$ , $f$ sei stetig differenzierbar und $( ) g1 g2 g = .. . gn$ : $S (_ Rn '--> R$ $(m < n)$ stetig differenzierbar. Ist $x0$ ein Extremalpunkt von $f$ unter den Nebenbedingungen $g(x) = o$ und sind $\~/ g1$ , $\~/ g2$ , $...$ , $\~/ gn-1$ linear unabhängig, so gibt es Zahlen $c1$ , $...$ , $cm (- R$ mit $m \~/ f (x ) = sum c \~/ g (x ) n j=1 j j j$ . Dies zusammen mit $g(x ) = o 0$ sind $n + m$ Gleichungen für die $n + m$ Unbekannten $x0$ und $c1$ , $c2$ , $...$ , $cn-1$ .

Betrachte:

|---------m--------------| | \~/ f (x )+ sum m \~/ g (x ) = o | 0 j=1 j j 0 | -------------------------|

m sum F (x1,...,xn,m1,...,mm) = f (x1,...,xn)+ mjgj(x1,...,xn) j=1

Berechne von $F$ die Extremwerte: Dazu müssen wir als erstes herausfinden, wo die stationären Stellen liegen.

m \~/ F (x ,m ,...,m ) = o = \~/ f(x)+ sum m \~/ g (x) = o x 1 1 m x j=1 j 1

\~/ mF (...) = o = g(x)

Beispiel:

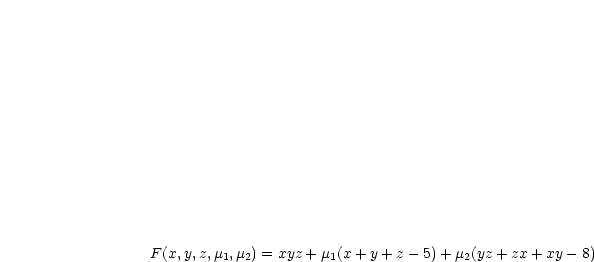
F(x,y,z,m1,m2) = xyz + m1(x+ y + z- 5)+ m2(yz + zx+ xy - 8)

Wir berechnen $\~/ x$ :

$yz + m1 + m2(z + y) = 0$
$xz + m1 + m2(z + x) = 0$
$xy +m1 + m2(x+ y) = 0$

Außerdem ist noch $\~/ m$ auszuwerten:

$x +y + z- 5 = 0$
$yz + zx + xy- 8 = 0$

Wir subtrahieren die zweite Gleichung von der ersten:

z(y- x)+ m2(y- x) = (y - x)(z + m2) = 0 ==> y = x oder z + m2 = 0

Durch Einsetzen in die vierte Gleichung erhalten wir $2x + z = 5$ und daraus $z = 5- 2x$ . Aus der fünften Gleichung folgt:

4 2 2x(5- 2x)+ x2 - 8 = 0 ==> x1 = 2 = y1, z1 = 1 oder x2 =-= y2, z2 = 3 3

(4 4 7) P1(2,2,1), P2 3,3,3

Zyklische Vertauschung der Variablen (Invarianz) $(x,y,z) '--> (y,z,x) '--> (z,x,y)$ ergibt:

( ) 4 7 4 P3(2,1,2), P4 3,3,3

( ) P5(1,2,2), P6 7, 4, 4 3 3 3

$P1$ , $P3$ , $P5$ sind Minima und $P2$ , $P4$ , $P6$ Maxima.

Beispiel:

Es soll $f (x1,x2,x3) = x21 + x22$ extremal (minimal) werden unter folgenden Nebenbedingungen:

g1(x1,x2,x3) = x3 = 0, g2(x1,x2,x3) = x23 -(x2 -1)3) = 0

[ 3] F(x1,x2,x3,m1,m2) = x21 + x22 + m1x3 +m2 x23- (x2- 1)

Wir berechnen $\~/ x$ :

$2x1 = 0$ $==>$ $x1 = 0$
$2 2x2- 3m2 (x2 - 1) = 0$ $==>$ $x2 = 0$
$m1 + 2x23m2 = 0$

Außerdem benötigen wir $\~/ m$ :

$x3 = 0$
$x23- (x2- 1)3 = 0$ $==>$ Mit der vierten Gleichung erhalten wir $x2 = 1$ .

$x2=0$ und $x2 = 1$ ergibt einen Widerspruch. Infolgedessen ist das Gleichungssystem nicht lösbar. Extremwerte liegen höchstens dort vor, wo $\~/ g1$ und $\~/ g2$ linear abhängig sind. Dies geht nur für $x2 = 1$ . Dann folgt also Lösung: $S(0,1,0)$ .