2.1 Differenzierbarkeit im Komplexen

Definition:

|----------------------------------------------------------------------------------------|
| |
| f(z)--f(z0)- |
|Es sei f : G (_ C '--> C, w = f(z). f heißt in z0 (- G differenzierbar, falls lz'-->imz0 z- z0 existiert. |
|Dann heiß t der Grenzwert die Ableitung von-f-an der-Stelle-z0 und wird mit f'(z0) bezeichnet. f heißt
|in z0 holomorph, falls f in einer Umgebung von z0 differenzierbar ist. Eine Funktion ist in einem Gebiet
|holomorph, wenn sie in jedem Punkt holomorph ist. |
-----------------------------------------------------------------------------------------

Satz 1:

|----------------------------------------------------------------------------------------|
| |
|f ist in z0 differenzierbar genau dann, wenn es ein A (- C gibt mit folgender Eigenschaft: |
| |
|f(z) = f(z0)+ A(z- z0)+ o(z- z0), z '--> z0 |
| ' |
|In diesem Fall ist A = f(z0). |
-----------------------------------------------------------------------------------------

Beweis:

lim f(z)--f(z0)--f'(z0)(z---z0)-= 0 <==> f(z)- f(z )- f'(z )(z- z ) = o(z-z ) z'-->z0 z- z0 0 0 0 0

Es gelten wie im Reellen alle Differentiationsregeln wie beispielsweise Produktregel, Quotientenregel, Kettenregel, Differenzieren von Potenzreihen. Wir schauen uns eine komplexe Potenzreihe an:

oo ( | |) f(z) = sum a (z- z )k,| z -z |< R : R =-----1 V~ ---- lim ||-an-|| k= k 0 0 lim sup n |an| n'-->o o |am+1 |

f'(z) existiert für alle z mit z - z₀ < R, und es gilt:

sum oo f'(z) = akk(z- z0)k-1 k=1

Das ist nun wieder eine Potenzreihe mit demselben Konvergenzbereich. Die Potenzreihe ist beliebig oft komplex differenzierbar. Jede Ableitung kann man berechnen, indem man gliedweise differenziert.

Es sei f : G G, w = f(z), u(x,y) = Ref(x + iy), v(x,y) = Imf(x + iy). Wir stellen uns nun die Frage, was die Differentiation von f für u und v bedeutet.

Definition:

|----------------------------------------------------------------------------------------|
| |
| 1.) f heißt reelldifferenzierbar, wenn u, v differenzierbar sind. |
| ---- |
| 2.) (@xf)(x + iy) = D1u(x, y)+ iD2v(x,y) |
| (@yf)(x + iy) = D2u(x, y)+ iD2v(x,y) |
-----------------------------------------------------------------------------------------|

\text{[math]}

u, v sind differenzierbar in (x₀,y₀) (z₀ = x₀ + iy₀):

u(x,y) = u(x0,y0)+(D1u) (x0,y0)(x-x0)+(D2u) (x0,y0)(y- y0)+o (||(x,y)- (x0,y0)||) (x,y) '--> (x0,y0)

v(x,y) = v(x0,y0)+(D1v)(x0,y0)(x- x0)+(D2v)(x0,y0)(y- y0)+o (|| (x,y)- (x0,y0)|| ) (x,y) '--> (x0,y0)

Nun schreiben wir die zweite Zeile komplex:

u(x,y) = u(x0,y0)+(D1u) (x0,y0)(x-x0)+(D2u) (x0,y0)(y- y0)+o (||(x,y)- (x0,y0)||) (x,y) '--> (x0,y0)

iv(x,y) = iv(x0,y0)+i(D1v)(x0,y0)(x- x0)+i (D2v)(x0,y0)(y-y0)+io(||(x,y) -(x0,y0)||) (x,y) '--> (x0,y0)

Durch Addition folgt nun:

f(x+ iy) = f(x0 + iy0)+ (@xf) (x0 + iy0)(x - x0)+ (@yf )(x0 + iy0)(y - y0)

Wir setzen folgendes ein:

1 - z = x+ iy,x = 2 (z + z)

1 z0 = x0 + iy0,y =- (z - z) 2i

Daraus folgt:

f ist in z0reell differenzierbar.

<==> f(z) = f(z0)+1 (@xf(z0)- i@yf(z0))(z-z0)+ 1(@xf(z0) +i@yf(z0))(z- z0)+o (| z- z0|),z '--> z0 2 2

Satz 2:

-----------------------------------------------------------------------------------------
| |
|Es ist w = f(z) in G holomorph. <==> f ist reell differenzierbar in G und es gilt: |
| |
|@xf(z)+ i@yf(z) = 0 A z (- G (*) |
| |
-----------------------------------------------------------------------------------------

\text{[math]}

Was bedeutet jedoch (*):

D u(x,y)+ iD v(x,y) = - iD u(x,y) +D v(x,y) 1 1 2 2

<==> D u(x,y) = D v(x,y) 1 2

<==> D1v(x,y) = - D2u(x,y)

Oder wie man in manch anderen Büchern findet:

ux = vy

vx = - uy

Dies sind die sogenannten Cauchy-Riemannsche Differentialgleichungen.

Satz 2 (andere Formulierung):

|----------------------------------------------------------------------------------------|
| (x ) (u(x, y)) |
|w = f(z) ist in G holomorph, falls das Vektorfeld y '--> v(x,y) differenzierbar ist und die Cauchy-
| |
|Riemannschen Differentialgleichungen in G erf¨ullt sind. |
| |
-----------------------------------------------------------------------------------------

Beispiel:

f(z) = z

u(x,y) = x,v(x,y) = - y

Eingesetzt in die Cauchy-Riemannschen-Differentialgleichungen ergibt:

D1u = 1 /= D2v = - 1

Die Differentialgleichungen sind nicht erfüllt. Daraus folgt, daß die Funktion nirgends holomorph ist.

Beispiel:

-- f(z) = |z|= V~ zz

|z|2 f(z) = z = z

-@-f = 0 @z

Bemerkungen:

f'(z ) -------- 0------- -------- 0-------- f(z) = f(z )+ 1(@ f(z )- i@ f(z ))(z- z)+ 1(@ f(z )+ i@ f(z ))(z-z )+o (| z- z |),z '--> z 0 2 x 0 y 0 0 2 x 0 y 0 0 0 0

Ist f in z holomorph, so hat man:
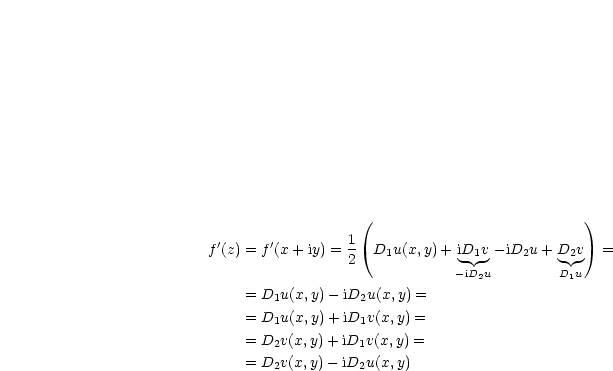$( ) 1 f'(z) = f'(x + iy) = 2 D1u(x,y)+ iD1v -iD2u + D2v = -iD2u D1u = D1u(x,y)- iD2u(x, y) = = D1u(x,y)+ iD1v(x, y) = = D2v(x,y)+ iD1v(x,y) = = D2v(x,y)- iD2u(x, y)$ (2.2)

$2 |f(x+ iy)| = u2x + u2y = u2x +v2x = v2y + v2x = v2y + u2y$

$' f(z) = 0 ==> f(z) = const.$
Die Ableitung dieser Funktion ist eine (2,2)-Matrix: $(D1u D2u) ( D1u D2u) w'(u,v) = D1v D2v (x,y) = - D2u D1u (x,y)$
Wir berechnen die Determinante:
$|----------------------| detw'(x,y) = |f'(x + iy)| 2| ------------------------$
Ist diese Funktionaldeterminante ungleich 0, so ist lokal injektiv.
$( ) u(x,y) = a detw'(x,y) /= 0 A (x,y) (- G ==> v(x,y) = b$
Es gilt: $\~/$ u(x,y) ^. $\~/$ v(x,y) = 0 $D1u(x,y)D1v(x, y)+D2u(x, y)D2v(x,y) = D1u(x,y)(- D2u(x,y))+D2u(x, y)D1u(x,y) = 0$

Interpretation:
$c,a = const.$

$u(x,y) = c } Diese Linien stehen senkrecht aufeinander. v(x,y) = a$

Beispiel:
$f(z) = z2 = x2- y2 + izxy$

$x2- y2 = u0$

$zxy = v0$
Diese stehen senkrecht aufeinander.

Beispiel:

Wir wollen zeigen, daß f(z) = e^-z² holomorph in ist.
$2 2 2 2 ( 2 2 ) f(x+ iy) = e-(x- y +2ixy) = e-(x -y)cos2xy +i e-(x- y )sin 2xy ----u(x,y)---- ------- ------- v(x,y)$
Die Cauchy-Riemannschen Differentialgleichungen sind erfüllt. u, v heißen harmonisch. Weiterhin muß gelten:
$/_\ u(x, y) = /_\ v(x,y) = 0$
$/_\$ ist der Laplace-Operator mit $/_\$ = $\~/$ ^. $\~/$ .
$uxx + uyy = 0,vxx + vyy = 0$

$D21u(x,y) +D22u(x,y) = D21v(x,y)+ D22v(x,y) = 0$
Als Übung kann man zeigen, daß man u, v beliebig oft differenzieren kann. Das heißt:
Mit f sind alle Ableitungen f⁽ⁿ⁾ holomorph.

Zunächst ohne Beweis:

Ist f einmal differenzierbar, so ist f beliebig oft differenzierbar. u, v sind beliebig oft stetig partiell differenzierbar, insbesondere gelte:
$D D u(x,y) = D D u(x,y) 1 2 2 1$

Satz:

$D1D1u = D1D2v, D1D2u = -D1D1v ==> /_\ v = 0$

$D2D1u = D2D2v,D2D2u = -D2D1v ==> /_\ u = 0$

Für den ladungsfreien Raum:
$/_\ .E = 0$

$/_\ × E = o ==> E = - \~/ f$
ist das Potential.
$0 = \~/ E = - \~/ . \~/ f = - /_\ f$
Es gibt eine holomorphe Funktion f mit Ref(x + iy) = (x,y).
$f (x + iy) = f(x,y) +iv(x,y)$
(x,y) = c sind die Äquipotentiallinien senkrecht zu v(x,y) = .

Beispiel:

Ist f(z) = e^-z² holomorph in ?

Satz 4:

Beweis:
$D1v = -D2u$

$D2v = D1u$

$( ) - D2u l¨osbar 2 \~/ v = D1u ------> D2(- D2u) = D1u ==> /_\ u = 0$

Beispiel:
$u(x,y) = x2- y2- y$
Gibt es eine holomorphe Funktion f mit Ref(x + iy) = u(x,y)? Wir überprüfen:
$\~/ u = 2+ (-2) = 0$
Die Gleichung ist erfüllt. Folglich gibt es so eine Funktion, die wir nun bestimmen wollen. Mit den Cauchy-Riemannschen Differentialgleichungen folgt:
$D v = 2y + 1 ==> v(x,y) = 2xy + x+ c(y) 1$

$D2v = 2x$
Mit der ersten Beziehung folgt:
$D2v(x,y) = 2x+ c'(y) ==> c(y) = c (- R : v(x,y) = 2xy + x+ c$

$2 2 2 f(x+ iy) = x - y - y + i(2xy + x+ c) ==> f(z) = z + iz + ic (c (- R)$
Setze:
$1 - 1 - x = 2 (z + z),y = 2i-(z - z)$

[next] [front] [up]