2 Komplexe Funktionen

[next] [prev] [prev-tail] [tail] [up]

Kapitel 2
Komplexe Funktionen

w = f(z),f : G (_ C '--> C

G ist ein Gebiet. Ein Gebiet hat die Eigenschaft, offen und zusammenhängend sein.

ex+iy = ex cos(y)+ iex sin(y)

( ) Re ex+iy = ex cos(y)

( x+iy) x Im e = e sin(y)

Ref(x+ iy) = u(x,y)

Imf (x+ iy) = v(x,y)

f(x+ iy) = u(x,y)+ iv(x,y)

2.1 Differenzierbarkeit im Komplexen
2.2 Umkehrfunktion/Der komplexe Logarithmus/Wurzeln
2.3 Der komplexe Logarithmus
2.4 Konforme Abbildungen: Möbiustransformationen
2.4.1 Möbiustransformationen (gebrochen lineare Funktionen)

Beispiel:

w = sin(z)

|sin(x)|< 1

Gesucht sei:

Re (sin(x+ iy)) = u(x,y)

Im (sin(x+ iy)) = v(x,y)

Wir wenden das Additionstheorem an:

( ) ( ) sin(x+ iy) = sin(x)cos(iy)+ cos(x) sin(iy) = sin(x)1 ei2y + e- i2y + cos(x) 1 ei2y- e-i2y = 2 2i = sin(x)cosh(y)+icos(x)sinh(y) u(x,y) v(x,y)

(2.1)

Veranschaulichung:

w = f(z)

Beispiel:

f(z) = ez,G = {z| 0 < Im(z) < 2p}

Durch dieses Gebiet wird ein Streifen im der komplexen Ebene dargestellt.

y (- (0,p) 0

z(t) = {t+ iy | t (- R} 0

ez(t) = eteiy0

Wir bewegen uns mit steigendem t auf einer Halbgerade von 0 nach .

z(t) = {x0 + it| a < t < 2p}

Es handelt sich um einen Kreis in der komplexen Ebene.

Definition:

|----------------------------------------------------------------------------------------|
| |
|Gegeben sei eine Funktion f : g < G '--> C, w = f(z), z0 (- G. f heiß t in z0 (- G stetig, falls
|lim f(z) = f(z0) oder falls die Funktion u(x,y) = Ref(x + iy), u(x,y) = imf (x + iy) in (x0,y0)
|z'-->z0 |
|(z0 = x0 + iy0) stetig sind. |
|Falls es zu jedem e > 0 ein d > 0 derart gibt, daßaus z (- G und |z- z0|< de, folgt|f(z) -f (z0)|< e.
-----------------------------------------------------------------------------------------

Beispiel:

f(z) = z2,u(x,y) = x2- y2

v(x,y) = zxy

f : G (_ C '--> C, w = f (z)

f(x+ iy) = u(x,y)+ iv(x,y)

1 w = f(z) = z + z,G = {z| Im(z) > 0}

Nun erhält man durch Umformung:

- w = f(z) = z +-z zz

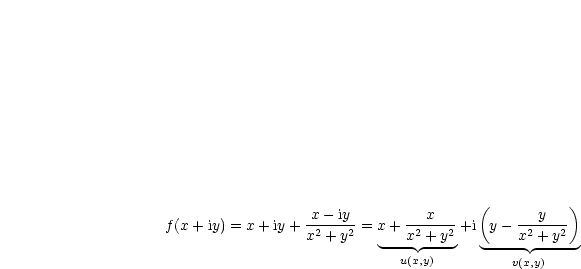
( ) -x--iy- --x---- --y---- f(x+ iy) = x+ iy+ x2 + y2 = x + x2 + y2 +i y - x2 + y2 --u(x,y)-- ----- ----- v(x,y)

Beispiel zur Stetigkeit:

z f(z) = z,z /= 0

Die Frage ist nun, ob f nach z = 0 stetig fortgesetzt werden kann.

z = reif

zli'-->m0 f(z) = ?

if -if 2if f(z) = re re = e

Wir suchen uns Punkte auf der ersten Winkelhalbierenden der komplexen Ebene:

1 ip zn = ne 4

p lim f (zn) = ei2 = i n'-->o o

Eine andere Folge von Punkten ist:

z = 1- n n

nl'-->imo o = f(zn) = 1

Nähert man sich auf zwei verschiedenen Wegen der Null an, so sind die Grenzwerte unterschiedlich. Daraus folgt, daß die Funktion f(z) nicht stetig sein kann.

[next] [prev] [prev-tail] [front] [up]