Folgende Begriffe wollen wir behandeln:
![]() \{0}
\{0}![]()
![]() \{0} sei schlicht.
\{0} sei schlicht.

Ist f(z) = sin![]() in z =
in z = ![]() differenzierbar? Betrachte g(z) = sinz in z = 0. Dort
ist sin(z) differenzierbar.
differenzierbar? Betrachte g(z) = sinz in z = 0. Dort
ist sin(z) differenzierbar.
Die reelle und die imaginäre Achse schneiden sich in Unendlichen unter dem Winkel
![]() .
.
Wir wollen zeigen, daß f(z) = ![]() :
: ![]()
![]()
![]() holomorph ist.
holomorph ist.
Also ist die Funktion holomorph.

Ersetze in der allgemeinen Kreis-Geraden-Gleichung ![]() |z|2 +
|z|2 + ![]() z +
z + ![]() z +
z + ![]() = 0 die
Variable z durch
= 0 die
Variable z durch ![]() . Man erhält somit durch Multiplikation mit |z|2:
. Man erhält somit durch Multiplikation mit |z|2:
Es handelt sich dabei also wieder um eine Gerade oder einen Kreis. Wir betrachten nun:

Folgende Abbildung nennt man Stereographische Projektion:
Es sei die Abbildung z ![]()
![]()
![]()
![]() gegeben. Was bedeutet diese auf der Kugel? Dazu
ersetze man in (*) z durch
gegeben. Was bedeutet diese auf der Kugel? Dazu
ersetze man in (*) z durch ![]() . Man erhält:
. Man erhält:
Wir schreiben dies in einer Verkettung von Abbildungen:
Bei der ersten Abbildung handelt es sich um eine Spiegelung an der (![]() ,
,![]() )-Ebene. Die
zweite Abbildung ist eine Spiegelung an der (
)-Ebene. Die
zweite Abbildung ist eine Spiegelung an der (![]() ,
,![]() )-Ebene. Auf der Kugel gehen somit
durch die Abbildung z
)-Ebene. Auf der Kugel gehen somit
durch die Abbildung z![]()
![]() Kreise über in Kreise. Nun gilt:
Kreise über in Kreise. Nun gilt:
Die Gleichung eines verallgemeinerten Kreises lautet:
Somit folgt:
Es handelt sich hier um eine Ebenengleichung. Schnitt mit ![]() 2 +
2 + ![]() 2 +
2 + ![]() 2 = 1 ergibt
einen Kreis. Der Kreis geht durch N, falls:
2 = 1 ergibt
einen Kreis. Der Kreis geht durch N, falls:
Kreis geht nicht durch N ![]()
![]() 0] Kreis in
0] Kreis in ![]()




Wir gehen nun über zu konformen Abbildungen.

Schlichtheit ist somit der Konformität übergeordnet. Was bedeutet aber Konformität
geometrisch?
Gegeben sei w = f(z), z ![]() G mit f'(z0)
G mit f'(z0)![]() 0.
0.
![]() (t) =
(t) = ![]() (t) + i
(t) + i![]() (t) ist die Tangentenkurve.
(t) ist die Tangentenkurve.
Eine Kurve mit dieser Eigenschaft hatten wir in HMII als regulär bzw. glatt bezeichnet. Diese Kurve soll nun abgebildet werden wobei wir erhalten:
Mittels der Kettenregel folgt:
Für das Argument folgt:
arg(![]() (t0)) gibt die Richtung von
(t0)) gibt die Richtung von ![]() in z0 an; arg(
in z0 an; arg(![]() (t0)) die Richtung des Bildes von
(t0)) die Richtung des Bildes von ![]() in z0.
in z0.
Daraus folgt, daß der Winkel erhalten bleibt. Dies formulieren wir in einem Satz:



Nun folgt der zentrale Satz in diesem Kapitel, nämlich der Riemannsche Abbildungssatz:


Eine Abbildung, die verallgemeinerte Kreise in verallgemeinerte Kreise abbildet, heißt kreistreu.



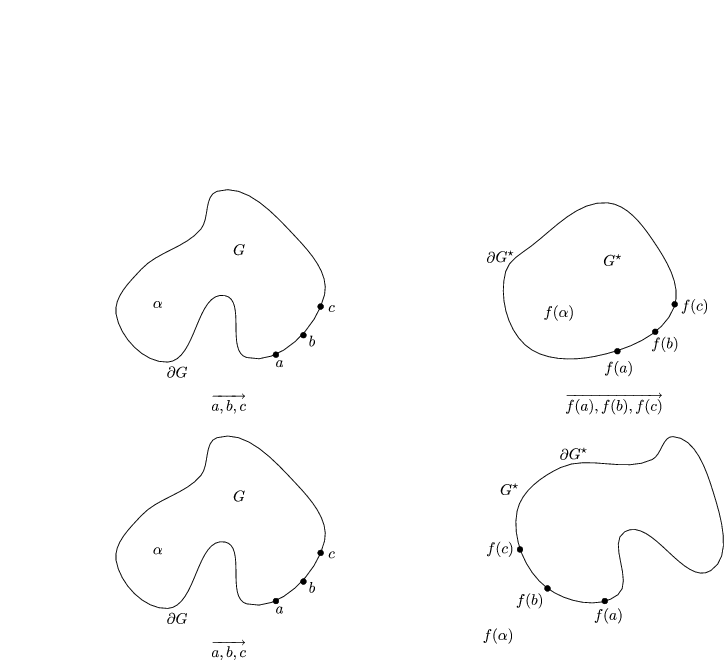
„Liegt ![]() links vom orientieren Rand
links vom orientieren Rand ![]() G, so liegt f(
G, so liegt f(![]() ) links vom orientierten Rand
) links vom orientierten Rand
![]() G* “.
G* “.
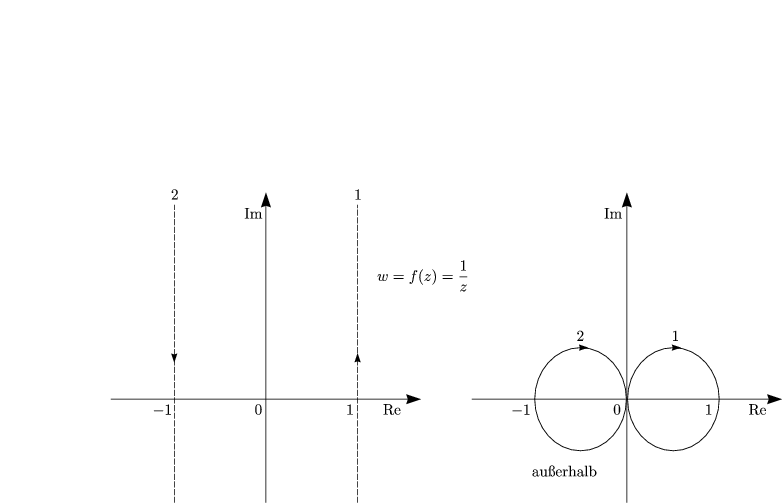


Wir differenzieren T(z):
Durch die Voraussetzung ad - bc![]() 0 wird somit ausgeschlossen, daß die Funktion
konstant ist.
0 wird somit ausgeschlossen, daß die Funktion
konstant ist.

T ![]() M ist somit kreistreu. Außerdem bildet (M,o) eine Gruppe:
M ist somit kreistreu. Außerdem bildet (M,o) eine Gruppe:




Es gibt nur diese Möbiustransformation: Angenommen, es gäbe S ![]() M mit
S(zj) = wj. Dann müssen wir beweisen, daß S = T gilt.
M mit
S(zj) = wj. Dann müssen wir beweisen, daß S = T gilt.
Es handelt sich somit um eine Möbiustransformation, welche 3 Fixpunkte hat. Also muß es die Identität sein.
Eine Möbiustransformation T mit T(![]() ) =
) = ![]() genügt der Bedingung:
genügt der Bedingung:
Unsere Forderung ist also:
Die dritte Bedingung ergibt a = c. Daraus folgt:
Mit der ersten Bedingung ergibt sich ![]() =
= ![]() :
:
Jetzt ist nur noch die zweite Bedingung zu erfüllen:
Die Umkehrabbildung lautet:


Um konkrete Formeln für Spiegelungen zu erhalten, setzen wir T = TK in die Definition ein, wobei man nun für die Spiegelung an einem Kreis erhält:
Für die Spiegelung an einer Geraden ergibt sich:
„Vernünftige“ Spiegelungen erfüllen folgende Bedingungen:
Wir überprüfen die erste Bedingung durch Einsetzen:
![]() k(z), z und a liegen auf demselben Halbstrahl, der von a ausgeht.
k(z), z und a liegen auf demselben Halbstrahl, der von a ausgeht.

Gesucht ist eine konforme Abbildung {z||z| < 1}![]() {w||w - 1| < 1} mit 0
{w||w - 1| < 1} mit 0![]()
![]() und
1
und
1![]() 0. Wir suchen also L mit folgenden Eigenschaften:
0. Wir suchen also L mit folgenden Eigenschaften:

Daraus folgt nun:
Unsere Forderung ist also:
Die dritte Bedingung ergibt a = c. Daraus folgt:
Mit der ersten Bedingung ergibt sich ![]() =
= ![]() :
:
Jetzt ist nur noch die zweite Bedingung zu erfüllen:
Die Umkehrabbildung lautet:


Um konkrete Formeln für Spiegelungen zu erhalten, setzen wir T = TK in die Definition ein, wobei man nun für die Spiegelung an einem Kreis erhält:
Für die Spiegelung an einer Geraden ergibt sich:
„Vernünftige“ Spiegelungen erfüllen folgende Bedingungen:
Wir überprüfen die erste Bedingung durch Einsetzen:
![]() k(z), z und a liegen auf demselben Halbstrahl, der von a ausgeht.
k(z), z und a liegen auf demselben Halbstrahl, der von a ausgeht.

Gesucht ist eine konforme Abbildung {z||z| < 1}![]() {w||w - 1| < 1} mit 0
{w||w - 1| < 1} mit 0![]()
![]() und
1
und
1![]() 0. Wir suchen also L mit folgenden Eigenschaften:
0. Wir suchen also L mit folgenden Eigenschaften:

Daraus folgt nun: