2.6 Die Wellengleichung auf einem endlichen Intervall

Es liegt das Problem

2 Lu = utt- c uxx = f(x,t) f¨ur < x < t, t > 0 { u(x,0) = f(x), ut(x,0) = y(x) f¨ur 0 < x < l (P) = P (f,f,y, B1,B2) u(0,t) = B1(t), u(l,t) = B2(t) f¨ur t > 0 [ux(0,t) = B1(t), ux(l,t) = B2(t)] f¨ur t > 0 [aux(0,t)+ a2u(0,t) = B1(t)]

vor. Würden Lösungen in C²((0,l),x(t > 0)) $/~\$ C¹([0,l] × (t > 0)) gesucht, so hat man die Verträglichkeitsbedingungen zu beachten.

' ' f(0) = B1(0), f(l) = B2(0), y(0) = B 1(0), y(l) = B 2(0)

1.Schritt:
U = U(x,t) wird gemäß U(0,t) = B₁(t), U(l,t) = B₂(t) gewählt. u(x,t) = U(x,t)+w(x,t) ist genau dann Lösung von (P), wenn w Lösung des Problems P( , , ,0,0) mit homogenen Randbedingungen ist.
2.Schritt:
Das Lösen von P(f,,,0,0) wird zerlegt durch Lösen der Probleme P₁(0,,0,0,0), P₂(0,0,,0,0), P₃(f,0,0,0,0). Die Summe der Einzellösungen u₁, u₂, u₃ ergibt sich Lösung von P(f,,,0,0).
3.Schritt: P₁(0,,0,0,0), P₂(0,0,,0,0)
Der Separationsansatz u(x,t) = (x)(t) liefert für n = 1, 2, ... zunächst:
$(1) (np ) (np ) (2) (np ) (np ) un (x,t) = sin l-x cos -l ct und un (x,t) = sin -l x sin -l ct$
Mit _n = ₀^l()sin d (n = 1, 2, ...) und _n = ₀^l()sin d (n = 1, 2, ...) erhält man als Lösungskandidaten für P₁(0,,0,0,0)
$oo sum (np ) (np ) u1(x,t) = ^fncos l-ct sin -l-x n=1$
und als Kandidaten für P₂(0,0,,0,0)
$sum oo l (np ) (np ) u2(x,t) = ----^ynsin ---ct sin --x n=1npc l l$
Dies sind Lösungen im oben formulierten (zweimal stetig differenzierbar) Sinn, falls für die Fourierkoeffizienten _n, _n erfüllt sind:
$( ) ( ) ^fn = O -14 ,y^n = O -13 f¨ur n '--> oo n n$
Dies gilt beispielsweise, wenn folgendes erfüllt ist:
$4 ' ' '' '' f (- C [0,l], f(0) = f(l) = f(0) = f (l) = f (0) = f (l) = 0$

$y (- C3[0,l], y(0) = y(l) = y'(0) = y'(l) = 0$
Man kommt mit deutlich schwächeren Bedingungen aus: siehe HM-Skript SCHNEIDER, KNAB: §17, Satz 17.57. Sind diese Bedingungen nicht oder nur teilweise erfüllt (die Reihen sollen konvergent sein), so spricht man wieder von verallgemeinerten Lösungen von P₁(0,,0,0,0) und P₂(0,0,,0,0). In diesem Sinn ist jetzt mit _n = c
$|----------------------------------------------------------------| | oo sum [ 1 ] (np ) | u0(x,t) = u1(x,t)+ u2(x,t) = ^fn cos(wnt)+ w--^ynsin(wnt) sin -l x | --------------------------n=1---------------n---------------------$
eine Lösung von P₁(0,,0,0,0) + P₂(0,0,,0,0) = P(0,,,0,0).

Führen wir diese Schritte nun ausführlich aus. Der erste Schritt ist eine Transformation der Randbedingungen zu Null. Wir verwenden den Ansatz u(x,t) = U(x,t) + w(x,t), welcher das Problem für w liefert:

Lw(x,t) = f(x,t)- LU (x,t) = f~(x,t)

w(x,0) = f(x)- U (x,0) = ~f(x); wt(x,0) = y(x)- Ut(x,0) = ~y(x)

w(0,t) = B1(t)- U (0,t)=!0 } w(l,t) = B2(t)- U(l,t)=!0 Bedingung an U

Wähle U(x,t) = B₁(t) + . Damit löst dann w folgendes Problem mit homogenen Randbedingungen:

Lw(x, t) = ~f(x,t)

w(x,0) = ~f(x), wt(x,0) = ~y(x)

w(0,t) = w(l,t) = 0

Nach Schritt 2 Wir zerlegen in P₁(0,,0,0,0), P₂(0,0,,0,0) und P₃(f,0,0,0,0):

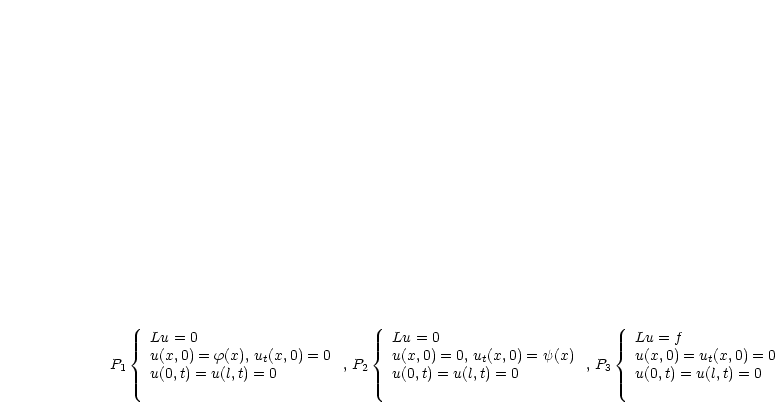
{ Lu = 0 { Lu = 0 { Lu = f P1 u(x,0) = f(x), ut(x,0) = 0 , P2 u(x,0) = 0, ut(x,0) = y(x) , P3 u(x,0) = ut(x,0) = 0 u(0,t) = u(l,t) = 0 u(0,t) = u(l,t) = 0 u(0,t) = u(l,t) = 0

Die Probleme P₁ und P₂ beschreiben die freie Schwingung einer eingespannten Saite (Separationsmethode). Bei P₃ handelt es sich um eine erzwungene Schwingung (äußere Kräfte) (DUHAMEL-Methode). Wir verwenden nach Schritt 3 den Ansatz u(x,t) = (x)(t) für P₁, P₂. Durch Einsetzen folgt dann:

a(x)¨b(t)- c2a''(x)b(t) = 0

¨ '' -12 b(t)-= a-(x)= m = const. c b(t) a(x)

'' a (x)- ma(x) = 0 f¨ur 0 < x < l, a(0) = a(l) = 0

¨b(t)- c2mb(t) = 0 fu¨r t > 0, b(0) = 0

(x)(0) = (x) (bleibt offen)
(x)(0) = 0
(0)(t) = (l)(t) = 0

Die Lösung des Randwertproblems ergibt sich zu (x) = exp(x). Daraus erhalten wir ² = und somit = ±. Die allgemeine Lösung lautet damit:

V~ -- V~ -- a(x) = C1exp ( mx)+ C2 exp(- mx)

Aus (0) = C₁ + C₁ 0 folgt C₁ = -C₂ und weiterhin:

|------------- V~ ---------- V~ ----| a(x)-=-C1[exp-(-mx)--exp-(----mx)]-

! V~ - V~ - V~ - V~ - a(l)= 0 = C1[exp( ml)- exp (- ml)] ==> [exp( ml)- exp(- ml)] = 0

Aus exp = 1 = exp erhalten wir l = ni und daraus wiederum = i.

|---------[---(np----)------(--np---)]-------(np--)-----------(np--)-----------------| an(x) = C1 exp --i.x - exp - --i.x = ~C sin --x , a(x) = sin--x f¨ur n = 1, 2, 3, ... -----------------l--------------l---------------l---------------l---------------------

Mit = - lautet das Problem für (t):

2 2 ¨b(t)+ c2n-p2--b(t) = 0 mitb˙(0) = 0 l

Diese Differentialgleichung besitzt folgende Lösung:

( ) bn(t) = cos npct f¨ur n = 1, 2, 3,... l

Wir erhalten schließlich das Gesamtergebnis:

|-----------(np--)----(np--)-----------------| |un(x,t) = sin -l x cos -l-ct f¨ur n = 1, 2, 3, ... ---------------------------------------------|

Des weiteren ist die Bedingung u(x,0) = (x) zu erfüllen. Wir machen dabei folgenden Ansatz: Gesucht sind Zahlen A_n (n = 1, 2, 3, ...) derart, daß für (x) gilt:

sum oo || sum oo (np ) (np )|| f(x) = Anun(x, t)|| = An sin ---x cos ---ct|| n=1 |t=0 n=1 l l |t=0

Falls die Reihe „genügend konvergent“ ist, gilt:

oo f(x) = sum A sin(np-x) n=1 n l

Hierbei handelt es sich gerade um die Fourierreihe von (x). Das ist erfüllt, wenn die A_n die Fourierkoeffizienten der nach -l < x < x ungeraden fortgesetzten 2l-periodischen Funktion (x) mit _[0,l] sind.

----------------------------------------------- | integral l | | 2 (np- ) | An = l f(q)sin l q dq = ^fn f¨ur n = 1, 2, 3, ... -------0---------------------------------------

Hierbei handelt es sich um die Fouriertransformierte. Die Lösung von P₁ ist dann:

|---------------------------------| | oo sum (np ) (np ) | u1(x,t) = ^fn sin l-x cos -l ct | ---------n=1-----------------------

u₁_xx, u₁_tt muß eine konvergente Reihe liefern, also muß _n=1n²| _n|² konvergieren. Als Übung kann durch viermaliges partielles Integrieren gezeigt werden:

integral t (np ) ^fn = f(q) sin --q dq 0 l

Beim Lösen des Problems P₂ erhalten wir analog folgende Bedingungen:

n2p2- n2p2-2 m = - l2 , b(t)+ l2 c b(t) = 0 mit b(0) = 0

Diese Gleichung wird gelöst durch:

(np ) bn(t) = sin-l-ct

|--(----)---(-----)-| un(x,t) = an(x)bn(t) =|sin npx sin npct | ------l--------l----|

Dies erfüllt dann alle Bedingungen bis auf (x) = u_t(x,0). Gesucht sind also Zahlen B_n mit:

oo sum ( ) y(x) = Bn npcsin np-x n=1 l l

Dies läßt sich wieder durch Fouriertransformation verwirklichen:

|--------------------------------------| | np 2 integral l (np ) | |Bn---= f^n mit ^yn = - y(q) sin --q dq| | l l0 l | ----------------------------------------

Damit gilt für das Problem P₂:

|----------------------------------| | sum oo ^y (np ) ( p )| u2(x,t) = --0-lsin --x sin n-ct | ---------n=1npc------l---------l----

Durch Addition der Einzellösungen u₁(x,t) und u₂(x,t), also durch

sum oo [ ^ ] ( ) (u1 + u2) = u0(x,t) = f^n cos(wnt)+ yn-sin(wnt) sin np-x n=1 wn l

ergibt sich die Lösung von:

Lu0 = 0

u0(x,0) = f(x), ut(x,0) = y(x)

u0(0,t) = u0(l,t) = 0

durch Superposition unendlich vieler Lösungen (Reihen). Hierbei handelt es sich um eine Entwicklung nach stehenden Wellen. Wir setzen nun:

^ ^fncos(wnt)+ ynsin(wnt) = ancoswn(t+ dn) wn

Wie berechnet man nun die _n und _n? Dazu benötigen wir erst einmal die Additionstheoreme:

an coswn(t+ dn) = an cos(wnt)cos(wndn)- an sin(wnt)sin(wndn)

Durch Koeffizientenvergleich ergibt sich:

y^n ^fn = an cos(wndn) und - w-= an sin(wndn) n

_n folgt aus der Division und anschließenden Anwendung des Arkustangens. Die _n erhält man durch Quadrieren und Addition beider Gleichungen. Daraus resultiert dann:

oo sum (np- ) u0(x,t) = an coswn(t+ dn)sin l x n=1

( ) u(0n)(x,t) = an coswn(t +dn)sin np-x l

Dabei handelt es sich um eine stehende Welle:

Knoten: $|------------------------------------------| |xk = lk f¨ur k = 1, 2, ..., n - 1 : u0(xk,t) = 0 A t| ------n------------------------------------|$
Bäuche: $|-------------------------------| | 2k+ 1 | |~xk = --2n--l f¨ur k = 0, 1, ..., n - 1 --------------------------------$

Bei u₀⁽ⁿ⁾(x,t) schwingt jeder Punkt mit derselben Frequenz _n = c. Des weiteren gilt ja bekanntlich _n = 2_n = c. Daraus folgen dann die möglichen Wellenlängen _n und Frequenzen _n auf der Saite der Länge l:

|---------------------------| cn = 2p-c = 2l, nn =-c-= n-c| -----wn----n-------cn----2l--

₁ = wird Grundfrequenz genannt; die anderen Frequenzen ergeben sich durch _n = n₁.

V~ -- V~ - T- n- T- rutt- Tuxx = 0 mit c = r und nn = 2l r

u₀ löst P(0,,,0,0), also u_tt - c²u_xx = 0. Die allgemeine Lösung der Gleichung ist u(x,t) = F(x - ct) + G(x + ct) (Entwicklung nach fortschreitenden Wellen).

u(n)(x,t) = ^f cos(w t)sin(np-x)+ ^yn-sin(w t)sin(np-x)= 0 n n c wn n l 1 [ (np ) (np )] 1^yn [ (np ) (np )] = 2 ^fn sin -l (x+ ct) + sin -l-(x - ct) + 2w-- cos -l-(x - ct) - cos l-(x+ ct) n

(2.8)

Für die Lösung von P₂(0,0,,0,0) gilt:

[ ] oo sum y^n (np ) u2(x,t) = wn-sin(wnt) sin -l-x n=1

Wir betrachten nun wieder P₃(f,0,0,0,0):

Lu = f(x,t) f¨ur 0 < x < l, t > 0 { u(0,t) = u(l,t) = 0 f¨ur t > 0 P3(f,0,0,0,0) = u(x,0) = ut(x,0) = 0 f¨ur 0 < x < l

Hier bietet sich dann die Methode von DUHAMEL an. Löse für 0 < < t das Problem P:

Lu = 0 f¨ur 0 < x < l, t > j { u(0,t) = u(l,t) = 0 f¨ur t > j P = u(x,j) = 0, ut(x,j) = f (x,j) f¨ur 0 < c < l

Man erhält dadurch also das Problem P₂ mit verschiedenen Anfangsbedingungen.

oo sum ^fn(j) (np--) u(x,t,j) = wn sin wn(t- j)sin l x n=1

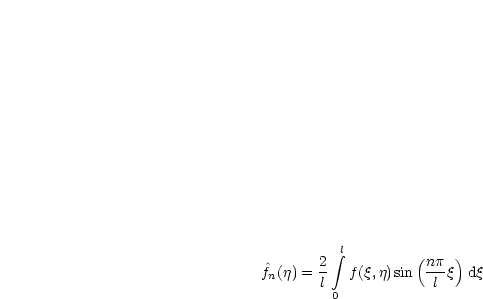
integral l ( ) ^fn(j) = 2 f(q,j)sin np-q dq l 0 l

Mit dem Prinzip von DUHAMEL erhält man nun:

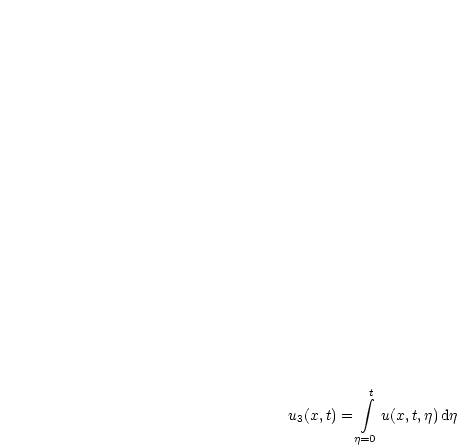
integral t u3(x,t) = u(x,t,j)dj j=0

|-----------------------------------------------------------------| | integral t integral l[o sum o 2 1 (np ) (np )] | u3(x,t) = -.---sin wn(t- j)sin --x sin ---q f(q,j)dqdj | | j=0 q=0 n=1-l-wn----------- -----l--------l---- | | G(x,q,t-j) | ------------------------------------------------------------------

G(x,,t - ) ist die sogenannte GREENsche Funktion des hier betrachteten Anfangswert-Randwert-Problems.

integral integral (LG)f = f(x,t)

Wir machen die Probe:

u - c2u = f(x,t) 3tt 3xx

@ integral t integral l[o o sum 2 (np ) (np )] u3tt(x,t) = -- -coswn(t- j)sin ---x sin ---q f (q,j)dqdj = @t0 q=0 n=1 l l l integral l [ ] integral t integral l[ ] oo sum 2 (np--) (np--) o sum o 2 (np- ) (np- ) = l sin l x sin l q f(q,j)dq - lwnsinwn(t- j)sin l x sin l q f(q,j) q=0 n=1 0 q=0 n=1

(2.9)

integral t integral l[ ] o sum o 2-1-n2p2- (np- ) (np- ) u3xx(x,t) = - lwn l2 sinwn(t- j)sin l x sin l q f(q,j)dqdj 0 q=0

integral t integral l[o sum o 2 1 n2p2 (np ) (np )] -c2u3xx(x,t) = + ----c2 -2--sin wn(t- j)sin --x sin --q f(q,j)dqdj 0 q=0 lwn l l l

Darüber hinaus gilt ja nun:

n2p2 1 1 c2--2-.---= w2n .--= wn l wn wn

Damit erhalten wir schließlich:

oo |_ integral l _| u -c2u = sum 2 f(q,t)sin (np-q) dq sin(np-x)= f(x,t) 3tt 3xx n=1 |_ l l _| l q=0

Es handelt sich gerade um die Fouriertransformierte von f(x,t). Die Probe geht folglich auf!

Problem P(0,, ,B1,B2):

Wir behandeln nun die zweite Methode zur Lösung von P(0,,,B₁,B₂):

1.Schritt:
Wir erstellen als erstes eine ungerade Fortsetzung von , nach [-l,0]. Ausgehend davon wollen wir eine auf ganz 2l-periodische Funktion erhalten. Das Problem ohne Randbedingungen kann mit der D'ALEMBERTschen Formel gelöst werden.
2.Schritt: Lösung von P(0,0,0,B₁,B₂): $utt- c2uxx = 0 f¨ur 0 < x < l, t > 0 { u(x,0) = ut(x,0) = 0 f¨ur 0 < x < l P (0,0,0,B1,B2) u(0,t) = B1(t), u(l,t) = B2(t)$
Der Ausgangspunkt ist nun:
$u(x,t) = f (t - x)+ g(t+ x-) c c$
Gesucht sind f und g. Wir definieren folgendes:
$B1(t) f¨ur t > 0 B2(t) f¨ur t > 0 -- { -- { B1(t) = 0 f¨ur t < 0 ;B2(t) = 0 f¨ur t < 0$

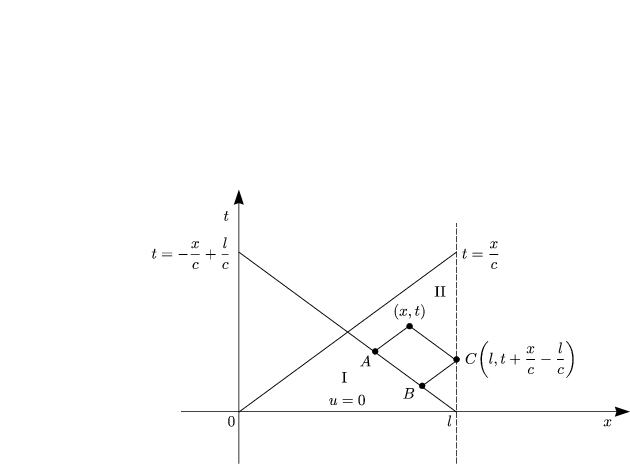
Im Gebiet I gilt:
$x- x- l u(x,t) = 0 f¨ur 0 < t < c und 0 < t < - c + c$
Für das Gebiet II folgt durch Umlaufen des eingezeichneten Parallelogramms:
$u(x,t)- u(A) +u(B) -u(C) = 0 0 0$

$( x l) x l x u(x,t) = B2 t+ c-- c f¨ur - c-+ c < t < c$
Daraus ergibt sich dann:
$( ) u(x,t) = B t + x- l f¨ur 0 < t < x 2 c c c$
Ein Vergleich mit oben liefert dann f(s) = 0 für s < 0. Wir setzen nun die entsprechenden Randbedingungen ein. Für x = 0 folgt:
$B1(t) = f(t)+ g(t)$
Daraus resultiert nun auch g(s) = 0 für s < 0. Gesucht sind f und g - definiert auf ganz - derart, daß u(xmt) = f + g Lösung wird. Für x = l erhalten wir außerdem:
$-- ( -l) ( l) B2(t) = f t- c + g t+ c$
Wir ersetzen in der obigen Darstellung für B₁(t) die Variable t durch t -:
$( ) ( ) ( ) B1 t- l = f t- l + g t- l c c c$
Durch Subtraktion der letzten beiden Gleichungen folgt dann:
$-- -- ( l) ( l) ( l) B2(t)- B1 t- c = g t+ c - g t- c =: p(t)$
Nun machen wir das gleiche Spiel mit B₂(t) mit der Substitution tt-:
$( ) ( ) B-(t) t- l = f t- 2l + g(t) 2 c c$
Auch hier ergibt sich wieder durch Subtraktion:
$-- -- ( l) ( 2l) B1(t)- B2 t- - = f (t)- f t- -- =: q(t) c c$
Es wir t durch t - 2n ersetzt und aufsummiert:
$sum k ( l) sum k [ ( l) ( l)] p t- 2nc = g t- (2n- 1) c -g t- (2n+ 1)c n=0 n=0$
Hierbei handelt es sich offensichtlich um eine Teleskopsumme folgender Bauart:
$sum l (an- an+1) = a0 - a1 + a1- a2 + a2 -a3 + ... n=0$
Angewendet auf unser Problem ergibt sich:
$sum k ( l) ( -l) ( l) p t- 2n c = g t+ c - g t- (2k+ 1)c n=0$
Wir machen an dieser Stelle die Ersetzung tt - und lösen nach g(t) bzw. f(t) auf:
$( ) k ( ) ( ) k ( ) g(t) = g t- 2(k+ 1)l + sum p t- (2n + 1)l , f(t) = f t -2(k + 1)l + sum q t- 2n l c n=0 c c n=0 c$
Wir lassen k laufen:
$( ) ( ) oo sum l sum oo -l g(t) = p t -(2n + 1)c , f (t) = q t- 2nc n=0 n=0$
Es folgt dann:
$[ ( ) ( )] sum oo x- l x- l u(x,t) = B1 t- c- 2nc - B2 t- c- (2n+ 1)c + n=0 oo [ ( ) ( )] + sum B2 t+ x- (2n+ 1)l - B1 t+ x-- 2(n+ 1)l = n=0 c c c c$ (2.10)

Schließlich erhalten wir:
$--------------------------------------------------------------- | ( ) sum oo [ ( ) -- ( )] | |u(x,t) = B1 t- x- + B1 t- x-- 2nl - B1 t+ x- 2n l + | | c n=1 c c c c | | sum oo [ ( x l) -- ( x l)] | | + B2 t + c- (2n +1)c - B2 t- c- (2n+ 1)c | -----------n=0-------------------------------------------------$ (2.11)

Wir machen die Probe. Dabei stellen wir fest, daß sowohl u(x,0) = 0 als auch u_t(x,0) = 0 erfüllt sind. Des weiteren gilt:
$-- u(0,t) = B1(t) -B1(t) f¨ur t > 0$

$( ) [ ( ) ( )] -- l oo sum -- l l u(l,t) = B1 t- c + B1 t- (2n+ 1)c - B1 t- (2n- 1)c + oo [ ( n=1) ( )] sum B2 t- 2nl - B2 t- 2(n+ 1)l n=0 c c$ (2.12)

Mit der Tatsache, daß es sich schon wieder um eine Teleskopsumme handelt, resultiert:
$--( l) --( l) -- -- u(l,t) = B1 t- c - B1 t- c + B2(t) = B2(t) = B2(t)$
Damit geht die Probe auf.

2.6.1 Transmissionsprobleme

Angenommen, wir haben zwei Saiten mit verschiedenen physikalischen Eigenschaften (, c), die aber an einer Stelle fest miteinander verbunden sind: Die Wellengleichungen für getrennten Probleme lauten dann:

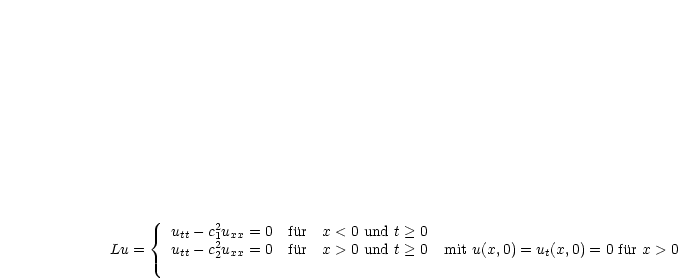
{ utt- c21uxx = 0 f¨ur x < 0 und t > 0 Lu = utt- c22uxx = 0 f¨ur x > 0 und t > 0 mit u(x,0) = ut(x,0) = 0 f¨ur x > 0

Die Lösung des Anfangswertproblems u_tt - c²u_xx = 0 (für x , t > 0) ist:

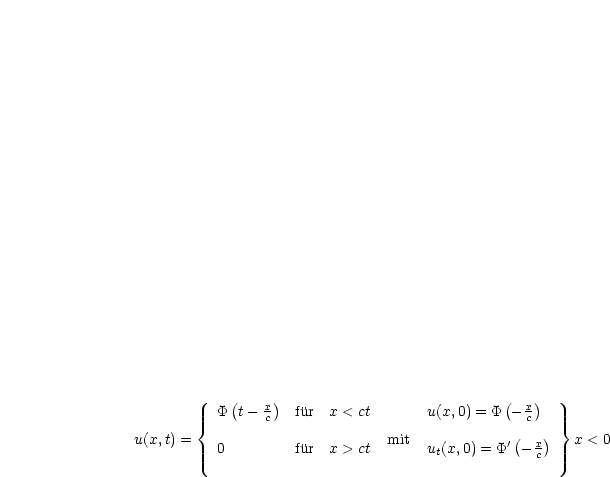
( x) ( x) { P t- c fu¨r x < ct u(x,0) = P - c } u(x,t) = mit '( x) x < 0 0 fu¨r x > ct ut(x,0) = P - c

u(x,0) = ut(x,0) = 0 f¨ur x > 0

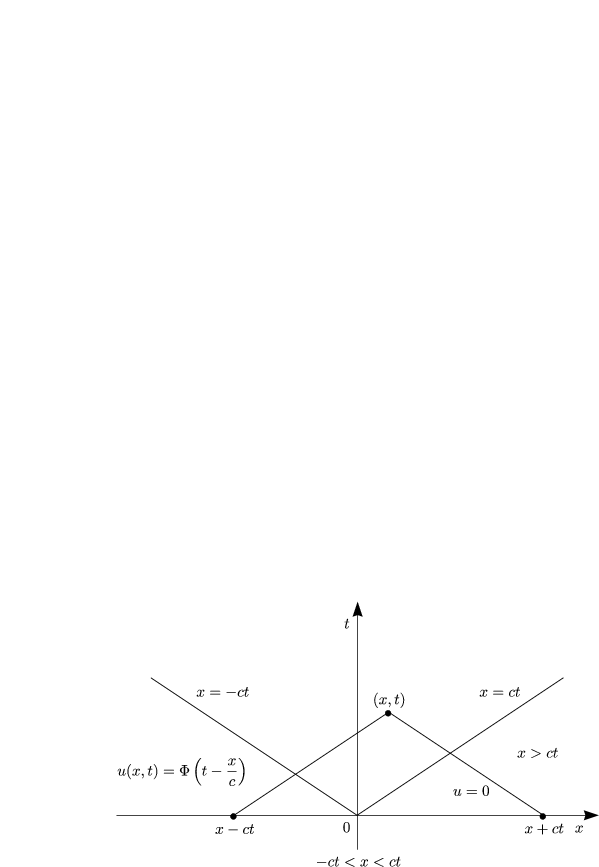
[ ( ) ] integral 0 ( ) ( ) ( ) u(x,t) = 1 P - x--ct + 0 + 1- P' - s ds = 1P t- x-+ 1P t- x-- 1P(0) 2 c 2cx- ct c 2 c 2 c 2- - !=0

Gesucht ist

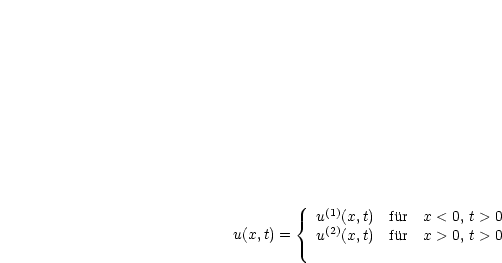
{ u(1)(x,t) f¨ur x < 0, t > 0 u(x,t) = u(2)(x,t) f¨ur x > 0, t > 0

mit u_tt -c₁²u_xx = 0 für t > 0, x < 0 und u_tt -c₂²u_xx = 0 für t > 0, x > 0 mit den folgenden Bedingungen:

( ) u(x,0) = P - x- f¨ur x < 0, u(x,0) = 0 f¨ur x > 0 c1

( x ) ut(x,0) = P' --- f¨ur x < 0, ut(x,0) = 0 f¨ur x > 0 c1

Die Übergangsbedingungen (Matching Conditions) stellen nun einen Zusammenhang zwischen den beiden Problemen her:

u(1)(0,t) = u(2)(0,t)

u(x1)(0,t) = u(x2)(0,t)

Wir können die allgemeine Lösung der beiden Gleichungen hinschreiben:

( ) ( ) u(1)(x,t) = F1 t- x- + G1 t+ x- c1 c1

( x ) ( x ) u(2)(x,t) = F2 t- c- + G2 t+ c- 2 2

x > c₂t: $u(2)(x,t) = 0 f¨ur x > c2t$
x < -c₁t: $( ) (1) x- u (x,t) = P t- c1$
0 < x < c₂t: $( ) (3) x- u (x,t) = F2 t- c2$
-c₁t < x < 0: $( ) ( ) u(1)(x,t) = P t- -x + G t+ -x c1 1 c1$

$P(0) = 0, F (0) = 0, G (0) = 0 2 1$

Zu bestimmen sind nun noch die Funktionen F₁ und G₁. Mittels der Übergangsbedingungen folgt nun:

u(1)(0,t) = P(t)+ G (t) != F (t) = u(2)(0,t) 1 2

u(1)(0,t)- 1-P'(t)+ -1G' (t)=!- -1F '(t) = u(2)(0,t) x c1 c1 1 c2 2 x

Man erhält dann folgende einfache Differentialgleichungen:

2c2 F2'(t) = c-+-c-P' 1 2

G'(t) = c2--c1P' 1 c1 + c2

Durch Integration erhält man dann:

2c2 F2(t) = c1-+c2P(t)

G1(t) = c2---c1P(t) c1 + c2

Also gilt:

x > c₂t: $u(2)(x,t) = 0 f¨ur x > c2t$
x < -c₁t: $( ) u(1)(x,t) = P t- x- c1$
0 < x < c₂t: $|-----------------(------)-| |u(3)(x,t) = -2c2--P t- x- | -----------c1-+-c2-------c2--|$
-c₁t < x < 0: $|--------------------------------------| | (1) ( x ) c2 - c1 ( x ) | |u (x,t) = P t - c1 + c1-+-c2-P t+ c1 | ---------------------------------------$

Man definiert nun Reflexions- und Transmissionskoeffizient wie folgt:

|----------------------| |T = --2c2--, R = c2--c1| -----c1 +-c2----c1-+c2-|

Hierbei gilt nun darüber hinaus R + 1 = T.

[prev] [prev-tail] [front] [up]