2.5 Verschiedene Anfangswert-Randwertprobleme

2.5.1 Fortsetzungsmethode

Wir behandeln die Probleme

Lu = u - c2u = f(x,t) f¨ur x > 0, t > 0 { u(x,t) t=tf(x)x,x u(x,0) = y(x) f¨ur x > 0 (Anfangsbedingung) P1(f,y, f,B) u(0,t) = B(t) t f¨ur t > 0 (Randbedingung)

und P₂(f,,,B), das aus P₁(f,,,B) entsteht, wenn man die Randbedingung durch u_x(0,t) = B(t) für t > 0 ersetzt.

1.Schritt: Es genügt, P₁(f,,,0) (P₂(f,,,0)) zu behandeln.
- Ist u₁ ( ₁) Lösung von P₁(f,,,0) (P₂(f,,,0)) und u₂ ( ₂) Lösung von P₁(0,0,0,B) (P₂(0,0,0,B)), so ist u₁ + u₂ ( ₁ + ₂) Lösung von P₁(f,,,B) (P₂(f,,,B)).
- Ist w () Lösung von P₁(-B'',-B(0),-B'(0),0) (P₂(-xB'',-xB(0),-xB'(0),0)), so ist u(x,t) = w(x,t) + B(t) ( (x,t) = (x,t) + B(t)) Lösung von P₁(0,0,0,B) (P₂(0,0,0,B)).
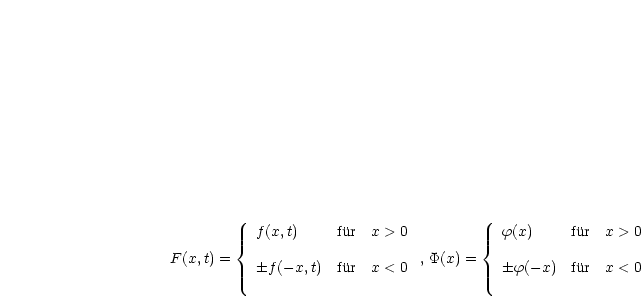
2.Schritt: Zur Lösung von P₁(f,,,0) (P₂(f,,,0)) setze f(0,t), , ungerade (gerade) auf ganz zu Funktionen F(•,t), , fort: ${ f(x,t) f¨ur x > 0 { f(x) f¨ur x > 0 F (x,t) = , P(x) = ± f(- x,t) f¨ur x < 0 ±f(- x) f¨ur x < 0$

${ y(x) f¨ur x > 0 Y(x) = ±y(- x) f¨ur x < 0$

Wir schreiben die Lösung in eine Form um, die F, und beinhaltet:
- 0 < t < : $1 1 x+ integral ct 1 integral t x+c integral (t- s) u(x,t) = -[P(x+ ct)+ P(x- ct)]+ -- Y(s)ds+ -- F(y,s)dyds 2 2cx-ct 2cs=0 y=x- c(t- s)$
- 0 < < t: $P(x+ ct) = f(x+ ct)$
  
  $P(x -ct) = - P(ct- x) = - f(ct- x)$
  
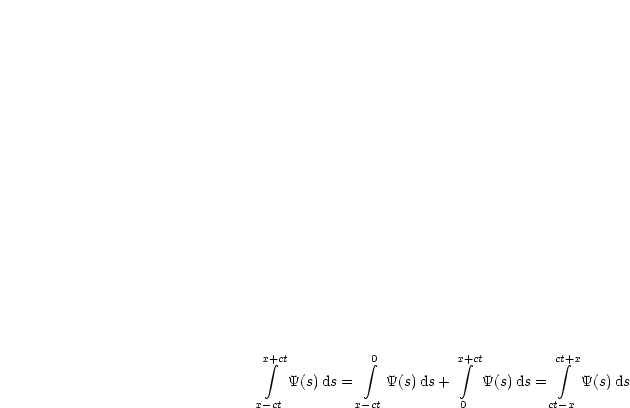
  $x integral +ct integral 0 x integral +ct ct integral +x Y(s)ds = Y(s)ds + Y(s) ds = Y(s)ds x-ct x-ct 0 ct-x$
  
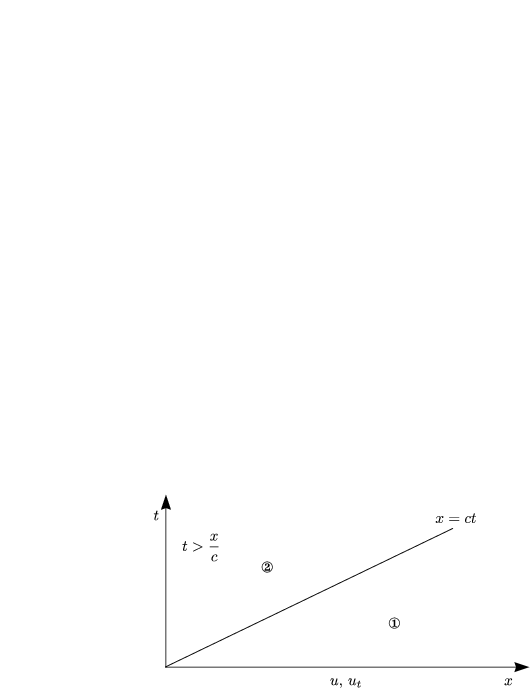
  $1 1 x+ integral ct 2 [P(x+ ct)+ P(x- ct)]+ 2c Y(s)ds f¨ur 0 < t < xc x- ct u(x,t) = { 1 1 ct integral +x -[P(x+ ct)- P(ct- x)]+ -- Y(s)ds f¨ur 0 < xc < t 2 2cct-x$
Die Lösung von P₁(f,,,0) (P₂(f,,,0)) ist also gegeben durch:
$|------------------------------------------------------------------------------------| | x+ integral ct integral t x+c integral (t-s) | u(x,t) = 1 (P(x - ct) + P(x+ ct))+ 1- Y(s)ds+ -1 F (y,s)dy ds f¨ur x > 0, t > 0 | 2 2c 2c | ---------------------------------x--ct-----------s=0y=x-c(t-s)--------------------------$
Drückt man auf der rechten Seite die Hilfsfunktionen , und F durch die gegebenen Funktionen , und f aus, so erhält man die Formel am Ende von Z11, bei der für 0 < t < der Form
$t x+c(t- s) 1- integral integral 2c f(y,s)dy ds s=0y=x-c(t- s)$
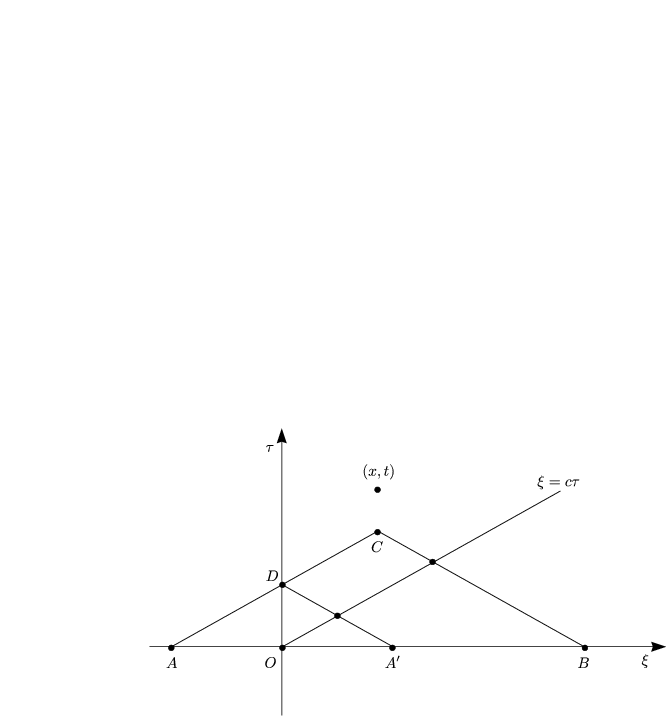
dazukommt und für 0 < < t der Term B wegfällt und das Integral über das Viereck (A’BCD)
$integral integral ( ) f(q,t)dqdt mit A = (ct-x,0), B = (x+ct,0), C = (x,t), D = 0,t- x A'BCD c$
dazukommt.

$integral integral integral integral integral integral = + = - + = /_\ (ABC) /_\ (AOD) [](OBCD) /_\ (OA'D) [](OBCD) [](A'BCD)$

Satz:

Es sei x₀ beliebig.

Sind , , F(•,t) ungerade bezüglich x₀, dann ist auch u(•,t) gemäß der D'ALEMBERTschen Formel ungerade bezüglich x₀. Das heißt, es gilt: $u(x0 + x,t) = - u(x0 - x,t) A t > 0, A x$
Daraus folgt dann u(x₀,t) = 0.
Sind , , F(•,t) gerade bezüglich x₀, dann ist auch u(•,t) gemäß der D'ALEMBERTschen Formel gerade bezüglich x₀. Das heißt, es gilt: $u(x0 + x,t) = +u(x0 - x,t) A t > 0, A x$
Daraus ergibt sich u_x(x₀,t) = 0.

Beweis von i.):

u1(x0+x, t) = f(x0+(x+ct))+f (x0 + (x - ct)) = - f((x0 - x)- ct)- f((x0- x)+ ct) = u1(x0- x,t)

x0+ integral x+ct - integral x+ct u2(x0 + x,t) = y(s)ds t==x0-s y(x0- t)dt = x0+x-ct -x-ct - integral x+ct (x0- integral x)+ct = - y(x0 + t)dt = - y(s)ds = u2(x0 - x,t) - x-ct s=x0+t (x- x)-ct 0

(2.7)

[next] [prev] [prev-tail] [front] [up]