[next] [prev] [prev-tail] [tail] [up]

2.4 Die Wellengleichung im halbunendlichen Intervall

Wir haben also folgendes Problem:

utt- c2uxx = f(x,t) f¨ur x > 0, t > 0

u(x,0) = f(x), ut(x,0) = Y(x)

Außerdem kann man eine Linearkombination verschiedener Randbedingungen vorgeben:

au(0,t)- bux(0,t) = B(t) f¨ur t > 0

ac(t) -bu (0,t) = B(t) fur t > 0 x ¨

PIC PIC

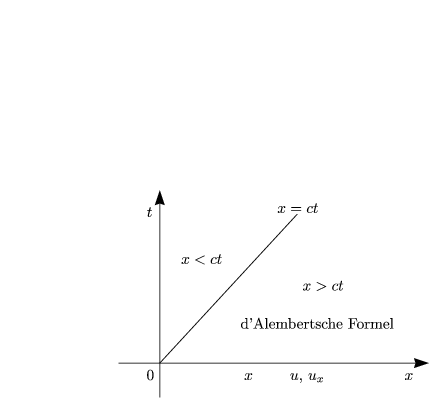
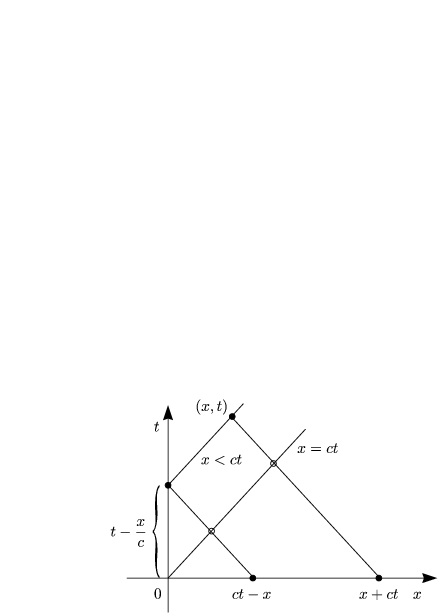
Wir integrieren also über das Trapez T, wobei wir das Integral mit F(x,t) bezeichnen wollen:

integral integral c integral t+x [ ( x-) ] [ ( x-)] Lu d(q,t) = - Y(s)ds+c [u(x,t)- f(x + ct)]- c u 0,t- c - u(x,t)+c f(ct- x)- u 0,t- c T ct-x

Mit der Abkürzung c(t) = u(0,t) erhalten wir durch Auflösen nach u(x,t):

ct+x 1- 1- integral 1 ( x) u(x,t) = 2cF(x,t)+ 2c Y(s)ds+ 2 [f(x+ ct)- f(ct -x)]+ c t- c ct- x

Wir betrachten nun den homogenen Fall f(x,t) = 0, womit auch F(x,t) = 0 folgt:

( ) ux(x,t) = 1-[Y(ct+ x)+ Y(ct- x)]+ 1 [f'(x+ ct)+ f'(x - ct)]- 1c' t- x- 2c 2 c c

Darüber hinaus gilt:

u(0,0) = xli'-->m0 u(x,0) = f(0), u(0,0) = tli'-->m0 u(0,t) = c(0)

1 1 a 1 ux(0,t) = -Y(ct)+ f'(ct)- -c'(t) != -c(t)- --B(t), c(0) = f(0) c c b b

Wir erhalten nun:

ca ( c ) c'(t)+ --c(t)+ - -B(t)- Y(ct)- cf'(ct) = 0 b --b-------- ----------- P(t)

Durch Lösung dieser linearen Differentialgleichung 1.Ordnung folgt:

integral t [ ]( ) c(t) = f(ct)+ exp a-c(s - t) c-B(s)+ Y(cs)- caf(s) ds b b b 0

|------------------------------------x integral +ct----------------------| | 1 -1 | | 2 [f(x+ ct) + f(x- ct)]+ 2c Y(s)ds f¨ur x > ct | | { x-ct | |u(x,t) = x+ct | | 1 -1 integral | | 2 [f(x+ ct) - f(x- ct)]+ 2c Y(s)ds f¨ur 0 < x < ct | | ct- x | ---------------------------------------------------------------|

Spezialfall f = f = Y = 0:
integral t [ ] c(t) = c- exp a-c(s - t) B(s) ds b 0 b

Es resultiert die Lösung des Problems:

|-------------------------------------------------------------| | 0 f¨ur x > ct | | | | { t integral -xc [ ( )] | u(x,t) = c- exp a- s - t+ x- B(s)ds f¨ur x < ct f¨ur b /= 0| | b 0 b c | | | --------------------------------------------------------------

Spezialfall a /= 0, b = 0, f = 0:
|------------------------------------x+ct-----------------------------------| | 1 1 integral | | 2 [f(x +ct)+ f(x -ct)]+ 2c Y(s)ds f¨ur x > ct | | { x-ct | u(x,t) = | | 1 1 ct integral +x 1 ( x ) | | 2 [f(x +ct)- Y(ct- x)]+ 2c Y(s)ds + aB t- c- f¨ur 0 < x < ct| | ct- x | | | ----------------------------------------------------------------------------

Als Übung kann folgendes gezeigt werden: u ist auch C2 (x > 0, t > 0), falls f, B (- C2, Y (- C1, af(0) = B(0), aY(0) = B'(0), c2f''(0) = 1 aB''(0)

[next] [prev] [prev-tail] [front] [up]