2.3 Stetige Abhngigkeit von den Daten

2.3 Stetige Abhängigkeit von den Daten

Wir haben also folgendes Problem:

Lu = utt- c2uxx = f(x,t) f¨ur x (- R und t > 0 { P0(f, Y, f) = u(x,0) = f(x), ut(x,0) = Y(x) f¨ur x (- R

Die Lösung kann mittels der D'ALEMBERTschen Formel berechnet werden:

1 1 x+ integral ct 1 integral t x integral +cs u(x,t) = -[f(x+ ct)+ f(x- ct)]+ -- Y(s)ds+-- f (y,t-s)dyds 2 2cx- ct 2cs=0y=x-cs

Es sei nun L₀ : C²() ×C¹() ×C¹( × (r > 0)) C²( × (t > 0)) die Lösung des Problems, also L₀(,,f) := u. L₀ ist „stetig“in ( ,, ) bedeutet dann nach HM I, daß es zu > 0 ein > 0 gibt derart, daß aus ||(,,f) - ( ,, || < folgt:

( ) ||L0 f~,Y~, ~f - L0 (f,Y,f)|| < e

Wir definieren eine Norm in C²(), C¹():

||c|| := sup{|c(x)||x (- R}

Für C¹( × t > 0) gilt:

||g||= sup {|g(x,t)|,x (- R,t > 0}

||(c,m,g)||:= ||c ||+ ||m||+ ||g||

Für eine Norm müssen folgende Eigenschaften gelten (siehe HM I):

||u||> 0, ||u|| = 0 nur für u = 0
||u|| = ||||u||
||u + v||<||u|| + ||v||

Diese Eigenschaften können als Übung gezeigt werden. Außerdem soll als Übung gezeigt werden, daß aus ||- || < , || -|| < , ||f - || < die Ungleichung ||u-|| < folgt mit folgendem :

e d <--------12 1 + t0 + 2t0

Andere Formulierung:

Aus der gleichmäßigen Konvergenz von _n, _n, f_n für n folgt:

( ~ ~) L0(fn,Yn, fn) '--> L0 ~f,Y,f

L₀ für , , ⁰ heißt verallgemeinerte Lösung von P₀( ,, ), falls es Folgen (_n), (_n), (f_n) mit (_n) ²(), (_n) C¹(), (f_n) C¹( × (t > 0) gibt mit L₀(_n,_n,f_n) L( ,, ) für n.

Wir fassen unsere Ergebnisse zusammen. Das Problem P₀(,,f) ist wohldefiniert:

Existenz (D'ALEMBERTsche Formel)
Eindeutigkeit (Satz 4)
Stetige Abhängigkeit von f, ,

Beispiel:

uxx + uyy = 0 im R2

Wir schauen uns zwei Lösungen der Gleichung an (Beweis durch holomorphe Funktionen):

v(x,y) = 0 und w(x,y) = 1sin(cx)cosh(cy) f¨ur c (- R c

Was passiert mit den Anfangsbedingungen?

v(x,0) = 0 und vy(x,0) = 0

1 w(x,0) = c sin(cx) und wy(x,0) = 0

Für gilt:

( ) 0, 1-sin(cx),0 '--> (0,0,0) c

Die Daten konvergieren also gegeneinander. Falls das CAUCHY-Problem für die Potentialgleichung wohldefiniert wäre, müßten w(x,y) v(x,y) für gelten. Das gilt nicht, da:

1 lim --sin(cx)cosh(cy) = oo f¨ur y > 0 c'-->o o c

Zur Struktur der Terme in der D'ALEMBERTschen Formel:

1 1 x+ integral ct 1 integral t x integral +cs u(x,t) = 2 [f(x+ ct)+ f(x- ct)]+ 2c Y(s)ds+2c f (y,t-s)dyds x- ct s=0y=x-cs

Wir führen nun folgende Bezeichnung ein:

1 x integral +ct (Iw)(x,t) := -- w(s)ds 2cx-ct

Hiermit erhalten wir:

integral t x+ integral cs @- 1- u(x,t) = @t [(If)(x,t)]+ (IY)(x,t)+ 2c f(y,t- s)dyds s=0 y=x-cs

integral t u(x,t) = @-[(If)(x,t)]+ (IY)(x,t)+-1 (If(•,s))(x,t- s)ds @t 2c s=0

Wir betrachten die Heaviside-Funktion:

1 f¨ur t > 0 { H(t) = 0 f¨ur t < 0

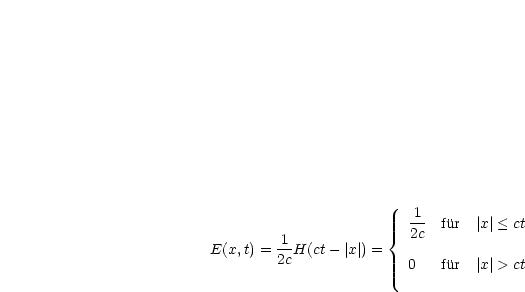
-1 f¨ur |x|< ct 1 { 2c E(x, t) = 2cH(ct- |x| ) = 0 f¨ur |x|> ct

1 (x,t) '--> E(x, t) = 2cH(ct- |x| )

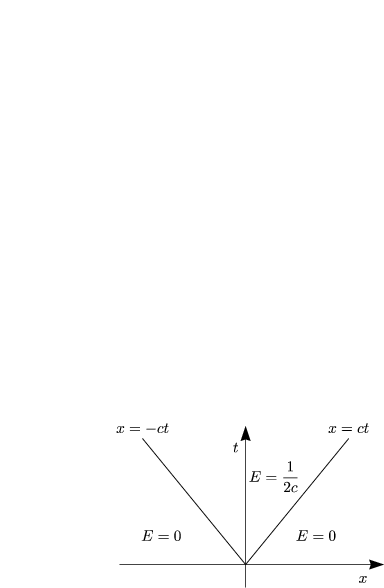
Wir führen das sogenannte Faltungsprodukt ein:

integral + oo (f *g)(x) = f(x -y)g(y)dy - oo

Mit der Substitution ys = x - y geht das Integral über in:

+ integral oo f (s)g(x- s)ds = (g *f)(x) - oo

Das Produkt ist kommutativ, man kann also f und g vertauschen. Die Variable, welche bei der Faltung eine Rolle spielt, sei • und t ein Parameter:

+ oo integral 1 integral (E(•,t)*Y) (x) = E(x - y,t)Y(y)dy = 2c Y(y)dy = (IY) (x,t) - oo |x-y|<ct

Die Funktion sei nun so gutartig, daß man die Zeitableitung in das Integral ziehen kann:

@t(If)(x,t) = @t(E( •,t)*f) (x) = (@tE(•,t)*f) (x)

+ integral o o integral oo 1 oo integral + integral oo (E *f)(x,t) = E(x - q,t -t )f(q,t)dqdt = -- H (c(t- t)- |x - q| )f(q,t)dqdt = q=- oo t=0 2ct=0q=- oo 1 integral integral = 2c- f(q,t)dqdt |x-q|<c(t-t)

(2.5)

-c(t- t) < x - q < c(t- t)

x - c(t- t) < q < x+ c(t- t) f¨ur 0 < t < t

Wir betrachten die -Funktion und deren Eigenschaften. Die -Funktion wird in der Distributionstheorie als Großvater der Distributionen bezeichnet.

0 f¨ur x /= 0 { d(x) = oo f¨ur x = 0

+ integral oo d(x)dx = 0 - oo

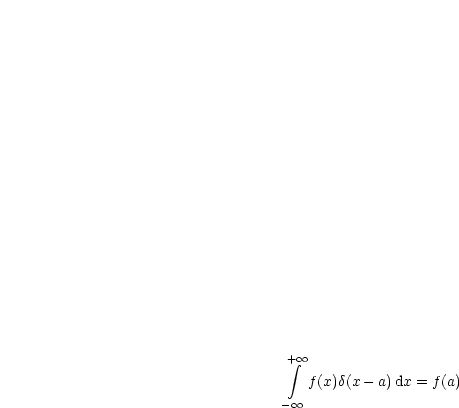
+ integral oo f(x)d(x- a)dx = f(a) - oo

(d*f )(x) = (f *d)(x) = f(x)

Die -Funktion ist also das neutrale Element der Faltung. u(x,t) = (x,t) löst u_tt - c²u_xx = f(x,t).

L(E *f )(x,t) = f(x,t)

(LE *f)(x,t) = (d*f) (x,t)

Durch Vergleich ergibt sich also LE = . E heißt Fundamentallösung, der Wellengleichung Lu = u_tt - c²u - xx, falls gilt „LE = “. Die GREENsche Funktion ist eine Fundamentallösung, welche bestimmte Randbedingungen erfüllt.

Wir notieren uns nochmals die D'ALEMBERTsche Formel:

x integral +ct x+ integral ct integral t x+c integral (t- s) u(x,t) = 1(f(x+ ct)+ f(x- ct))+ 1- Y(x)ds + 1- Y(s)ds+ 1- f(y,s) ds 2 2c 2c 2c ------------------------ x-ct-----------x-ct------- s=0 y=x-c(t-s) R(x,t)

Außerdem betrachten wir folgendes Problem (siehe Aufgabe 2 auf 5.Übungsblatt):

utt- uxx + u+ 2ut = 0

utt- uxx = - u- 2ut = T-(u,ut)(x,t) f(x,t)

Ein Iterationsverfahren bietet sich hier an:

u(x,t) = R(x,t)+ ~T(u,ut)(x,t)

u(n)(x,t) = R(x, t)+ T~(u(n-1),u(nt-1))(x,t)

Hier setzt man dan u⁽⁰⁾(x,t) = 0.

2.3.1 Einige Beispiele/DARBOUX-Problem, GAUSAT-Problem,
Charakteristisches Problem

Besonders in der Gasdynamik sind diese Beispiele wichtig.

DARBOUX-Problem $Lu = utt- c2uxx$
Die Charakteristiken sind x = ±ct + .

$integral integral Lu(x,t)dxdt = 2c [u(A) -u(B) + u(C)- u(D)] (ABCD)$
Es seien im folgenden a, b > 0 und konstant.
$Lu = f(x,t)$

$( x) u x,c- = f1(x) f¨ur 0 < x < b$

$( x) u x,- c- = f2(x) fu¨r - a < x < 0$
Des weiteren soll gelten:
$f1(0) = f2(0)$
Man spricht hier von einer Verträglichkeit von ₁ und ₂.

Man erhält dann, was wir hier nicht explizit vorrechnen, für die Koordinaten der Punkte A und B:
$( ) ct-+-q-ct +-q B = 2 , 2c$

$(q - ct q- ct) A = --2--,- -2c---$
Wir integrieren nun Lu = f über das Parallelogramm (0,B,(,),A).
$integral integral [ (ct + q) (q - ct )] f(x,t)d(x,t) = 2c f1(0) -f1 ------ + u(q,t)- f2 ------ 2 2$
Durch Auflösen erhält man nun u(,).
$ct +-q 0 < 2 < b <==> - ct < q < 2b- ct$

$q--ct- -a < 2 < 0 <==> ct- 2a < q < ct$
Wir betrachten das Anfangswert-Randwertproblem:
$u - c2u = f(x,t) tt xx$

$ut(x,0) = f1(x) fu¨r 0 < x < 2x0$

$( ) u x, x- = f2(x) f¨ur 0 < x < x0 c$

$( ) A = (q- ct,0) und B q +-ct, q +-ct 2 2c$

$integral integral Lu(x,t)dxdt = 2c [u(A) -u(B) + u(C)- u(D)] (ABCD)$

$integral integral gf Lu d(x,t) = [- utdx - uxdt] G @G$
- Integration über +-Charakteristik $N integral _O_ = - c[u(N )- u(M )] M$
- Integration über --Charakteristik $integral N _O_ = +c [u(N )- u(M )] M$
$q-ct integral integral integral I = f(x,t)d(x,t) = - f1(x)dx- c[u(q,t)- u(q- ct,0)]+ [ ( ) 0 ] [ ( )] q +-ct q +-ct + c f2 2 - u(q,t) - c f2(0)- f2 2$ (2.6)

Wir integrieren nun über (A,B,(,),C):
$integral integral [ ( ) ( )] f (x,t)dxdt = 2c u(q - ct,0)- u(q,t)+ f q +-ct - f q--ct- 2 2 2 2$
u(,) erhält man nun, indem man u( - c,0) eliminiert.
$0 < q-+-ct-< x0 2$

$0 < q- ct < 2x 0$
GAUSAT-Problem
Für ct < x < sei folgendes Problem gegeben:
$Lu = utt- c2uxx = 0$

$u(x,0) = f(x)$

$u(ct,t) = g(t) fur t > 0 ¨$

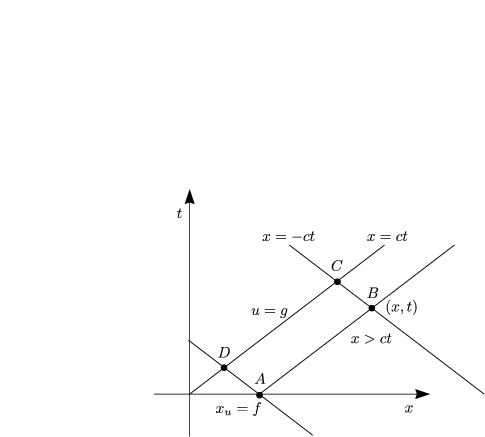
Man erhält somit durch Einsetzen der Anfangsbedingungen:
$u(x,t) = F (x + ct) +G(x - ct)$

$f(x) = F (x)+ G(x)$

$g(t) = F (2ct)+ G(0)$
Damit können wir bestimmen:
$( ) F (x) = g -x + G(0) 2c$

$( ) G(x) = f(x)- g -x + G(0) 2c$
Dann erhält man die allgemeine Lösung, da G(0) verschwindet:
$|----------------------------------------------| | ( 1 ) ( 1 ) | u(x,t) = g 2c (x+ ct) + f (x- ct) - g 2c (x- ct) | ------------------------------------------------$
Durch eine Probe kann nun noch überprüft werden, daß die Anfangsbedingungen wirklich erfüllt sind. Wenn die Gleichung inhomogen ist, gehen wir folgendermaßen vor:
$Lu = utt- c2uxx = h(x,t)$

$u(x,0) = f(x)$

$u(ct,t) = g(t) f¨ur t > 0$
Wir führen eine Integration über das charakteristische Parallelogramm durch:
$|-----------------------------------------------------------------| | ( 1 ) ( 1 ) integral integral | u(x,t) = g 2c (x+ ct) + f (x- ct) - g 2c (x - ct) + h(q,t)d(q,t)| | (ABCD) | -------------------------------------------------------------------$
Betrachten wir folgendes Problem:
$utt- c2uxx = 0$

$u(x,0) = f (x) fur 0 < x < a 1 ¨$

$( x) u x,b c = f2(x) fu¨r 0 < x < a$
Für 0 < < 1 gilt dann ₁(0) = ₂(0).

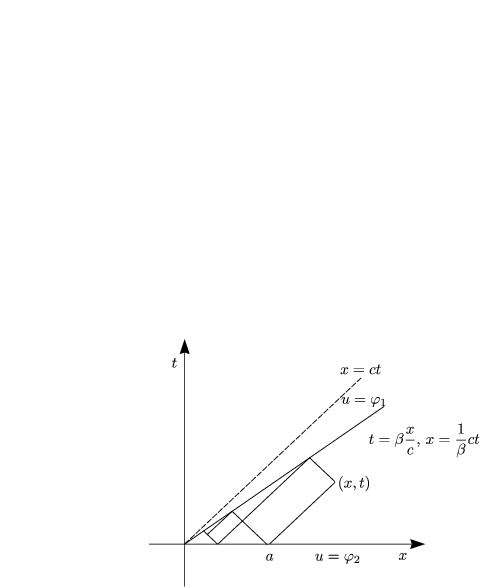
Man kann somit eine Iteration aufstellen. Man erhält dann eine unendliche Folge immer kleiner werdender charakteristischer Parallelogramme. Wir wollen jedoch nun anders vorgehen. Dazu notieren wir uns die allgemeine Lösung:
$u(x,t) = F (x + ct) +G(x - ct)$
Durch Einsetzen der ersten Bedingung folgt:
$f1(x) = F(x)+ G(x)$

$f2(x) = F ((1+ b)x)+ G ((1 - b)x)$
Dann erhalten wir aus der ersten Gleichung:
$F ((1 + b)x) = f1((1+ b)x)- G ((1+ b)x)$
Mit der zweiten Gleichung ergibt sich dann:
$f2(x)- f1((1+ b)x) = G ((1 - b)x)- G ((1+ b)x)$
Wir führen nun neue Bezeichnungen ein:
$1--b- (1+ b)x =: X, a = 1+ b f¨ur 0 < b < 1 <==> 0 < a < 1$
Damit folgt dann:
$( X ) (1 - b ) f2 ----- - f1(X) = G -----X - G(X) 1 +b 1+ b$

$( ) f -X--- - f (X) = G(aX) - G(X) 2 1+ b 1$
Die linke Seite ist uns natürlich immer bekannt; wir setzen diese gleich P(X) und erhalten dann folgende Funktionalgleichung:
$P (X) = G(aX) - G(X) mit 0 < a < 1$
Wir multiplizieren die Gleichung mit -1:
$-P (X) = G(x)- G(aX)$
Wir betrachten dies an der Stelle X:
$-P (aX) = G(aX) - G(a2X)$

$2 2 3 - P(a X) = G(a X) - G(a X)$
Wir addieren diese P, wobei sich eine Teleskopsumme ergibt:
$sum n - P(ajX) = G(x)- G(an+1X) j=0$
Aus der Stetigkeit von G folgt:
$sum oo G(X) - G(0) = - P (ajX) j=0$

$sum oo F(x) = f1(x)- G(0) + P (ajX) j=0$

$|------------------ oo ---------------- oo ------------| | sum ( j ) sum j | u(x,t) = f1(x+ ct)+ P a (x + ct) - P (a (x - ct))| -------------------j=0--------------j=0-------------$
Als Übung kann man Bedingungen an ₁ und ₂ stellen, so daß die Summe konvergent ist.
Beispiel:

Es sei ₁(x) = 0 und ₂(x) = x². Dann erhalten wir:
$j ( ajX )2 2j X2 P(a X) = 1-+-b = a .(1+-b)2$
Dann erhalten wir folgendes geometrische Reihe, deren Wert wir einfach berechnen können (siehe HM I):
$sum oo [ ] |---| u(x,t) = a2j ---1---[(x+ ct)2 -(x - ct)2] = --4xct-.---1-- = -cxt| j=0 (1 + b)2 (1+ b)2 1 - a2 b----$