2.2 Eindeutigkeit der Cauchyschen Anfangswertaufgabe: Energieintegralmethode

[next] [prev] [prev-tail] [tail] [up]

2.2 Eindeutigkeit der CAUCHYschen Anfangswertaufgabe: Energieintegralmethode

Es geht wieder um folgendes Problem:

Lu(x,t) = f(x,t) fu¨r x (- R und t > 0

u(x,0) = f(x), u (x,0) = Y(x) mit x (- R (*) t

Das Problem (*) besitzt genau eine Lösung, welche durch die D'ALEMBERTsche Formel gegeben ist.

Erste Möglichkeit zur Begründung:
Ist eine weitere Lösung, so gilt für w = u -:
$Lw = 0, w(x,0) = wt(x,0) = 0$
Satz 3 liefert dann w(x,t) = 0.

Satz 4:

$|----------------------------------------------------------------------------------------| | | |F¨uru (- C2(R × (0,T )) /~\ C1 (R × [0,T))gelte utt- c2uxx = 0f¨urx (- R,0 < t < T. Es sei(x0,t0),x0 (- R, |t0 (- (0,T ) beliebig aber fest. Aus u = ut = 0 folgt dann auf A(x0,t0), daß u = 0 im Bestimmtheitsgebiet |B(A(x0,t0)) ist ((x,t) = 0 A (x,t) (- B). | -----------------------------------------------------------------------------------------$

\text{[math]}

|_ _| integral l V~ ----- U = m .L¨angen¨anderung = m . |_ 1+ u2x dx- l _| 0

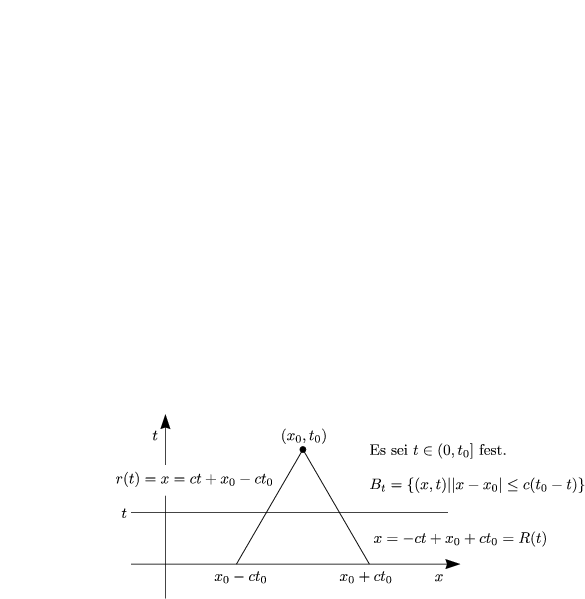
Dieser Ausdruck gilt nur, wenn wir kleine Schwingungen betrachten. Wir entwickeln also die Wurzel, wobei wir nur einem Term behalten:

V~ 1-+-u2-= 1+ 1u2 + O(x4) x 2 x

Daraus folgt dann:

integral l 1 U = m 2u2xdx 0

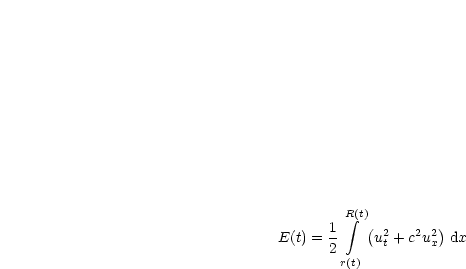
R integral (t) E(t) = 1 (u2t + c2u2x)dx 2 r(t)

integral E(t) > 0 A t und E(0) = 1 (u2(x,0)+ c2u2(x,0))dx = 0 2 x t A(x0,t0)

Unser Ziel ist, zu zeigen, daß E(t) = 0 für 0 < t < t₀. Das Vorgehen hierzu ist, (t) zu bilden:

|_ R integral (t) _| ˙ 1 ˙ ( 2 2 2 ) ( 2 2 2 ) 1 ( 2 ) E(t) = 2 |_ R(t) ut (R(t),t)+ c ux(R(t),t) - ˙r(t) ut (r(t),t)+ c ux(r(t),t) + 2 2ututt +2c uxuxt dx _| = r(t) R integral (t) = - 1c[(u2+ c2u2)(R(t),t)+ (u2+ c2u2)(r(t),t)]+ 1 (2ututt + 2c2(uxut) - utuxx)d = 2 t x t x 2 x r(t) [( ) ( ) ] R integral (t)[ ( ) ] = - 1c u2t + c2u2x (R(t),t)+ u2t + c2u2x (r(t),t) + 1 2ut utt -c2uxx + 2c2(uxut)x dx = 2 2 r(t) 1 [( ) ( ) ] = - -c u2t + c2u2x (R(t),t)+ u2t + c2u2x (r(t),t) + c2[(uxut)(R(t),t)- (uxut)(r(t),t)] = 2 [( ) ( ) ] = - 1c u2t + c2u2x- 2cuxut (R(t),t)+ u2t + c2u2x + 2cuxut (r(t),t) = 2 [ ] = - 1c (ut- cux)2 (R(t),t) + (ut + cux)2(r(t),t) < 0 2

(2.4)

Da E(t) > 0, E(0) = 0 und (t) < 0 gilt für 0 < t < t₀, haben wir somit folgende Erkenntnis gewonnen:

integral E(t) = 0 = 1 (u2+ c2u2)dx 2 t x Bt

Damit ist also u(x,t) = const. (x,t) B. Mit u(x,0) = 0 folgt dann u(x,t) = 0 (x,t) B.

[next] [prev] [prev-tail] [front] [up]