2.1 Die Parallelogrammidentitt

2.1 Die Parallelogrammidentität

2 Lu = utt- c uxx

Ein charakteristisches Parallelogramm hat nur charakteristische Seiten.

₊: x - ct = ₁ = const.
_-: x + ct = ₂ = const.

Vorbereitungen:

K sei Kurve in der (x,y)-Ebene. Wir wollen folgendes Integral berechnen:

integral I = [h(x,y)dx + g(x,y)dy] K

Dazu benötigen wir eine Parameterdarstellung (t) der Kurve mit t [a,b]:

( ) x(t) r(t) = y(t)

Haben wir diese Parameterdarstellung, so kann das Integral einfach berechnet werden:

integral b integral b (h(x,y)) ˙ g(x,y) I = [h(x(t),y(t))˙x(t)+ g(x(t),y(t))˙y(t)] dt = v(r(t)).r(t)dt mit v(x,y) = t=a t=a

Wir stellen nun die Charakteristiken mittels Parameterdarstellung dar:

( ) ( ) ct+ g1 ˙ c r(t) = t ,r(t) = 1

(- ct+ g2) ( - c) r(t) = t , ˙r(t) = 1

Nun gilt mittels der Kettenregel:

u = u(r(t)), d-u = \~/ u(r(t)).˙r(t) = cu + u g+ dt g+ x t

ug- = u(r(t)), d-ug- = -cux + ut dt

Dann benötigen wir noch den Gaußschen Integralsatz in der Ebene:

|----------------------------------------------------------------------------------------|
| |
|G sei Gebiet in der (x,t)-Ebene, @2G-sei außerdem positiv orientiert und gen¨ugend gutartig. Des weiteren
|sei P = P(x,t), Q = Q(x, t) (- C (G) gegeben. Dann gilt: |
| integral integral gf |
| [Qx---Pt] d(x,t) = [P dx + Qdy] |
|G Lu @G |
-----------------------------------------------------------------------------------------

\text{[math]}

Angewendet auf unser Problem resultiert:

integral integral ( 2 ) integral integral [( 2 ) ] gf ( 2 ) utt- cuxx d(x,t) = -c ux x- (-ut)t d(x,t) = -utdx - c uxdt G G @G

Wir gehen nun aus von einer Funktion u C²()

integral N g+ : w = - c(u(N )- u(M )) M

integral ~N g : w = c(u(N ~)- u(M~)) - ~M

G = (ABCD) sei charakteristisches Parallelogramm in . Dazu berechnen wir das Integral I:

integral integral gf I = Lu dxdt = (- utdx- c2uxdt)= GB @G C D A integral ( 2 ) integral ( 2 ) integral ( 2 ) integral ( 2 ) = - utdx -c uxdt + -utdx - cux dt + -utdx - cux dt + -utdx - cux dt = A B C D integral B integral C integral D integral A = - c (ut + cux) dt+ c (ut -cux) dt- c (ut + cux) dt+ c (ut - cux) dt = A B C D B C D A integral -d integral -d integral -d integral -d = - c dtug+ dt+ c dtug- dt- c dtug+ dt+ c dtug- dt A B C D

(2.1)

integral integral Lu d(x,t) = -c[u(B)- u(A)]+ c[u(C)- u(B)]- c[u(D)- u(C)]+ c[u(A)- u(D)] = G = 2c[u(A)+-u(C)---u(B)--u(D)]| ----------------------------

(2.2)

Wir formulieren dies als Satz:

Satz 1:

|----------------------------------------------------------------------------------------|
| 2 2 -- |
|Es sei Lu = utt- c uxx und G = (ABCD) sei charakteristisches Parallelogramm f¨ur L. Ist u (- C (G),|
|so gilt: |
| integral integral |
| Lu(x,t)d(x,t) = 2c(u(A) + u(C)- u(B) - u(D)) |
(ABCD) |
| |
-----------------------------------------------------------------------------------------

Satz 2:

|----------------------------------------------------------------------------------------|
|G (_ R2(x,t) sei ein Gebiet, wobei u (- C2(G). Dann gilt: |
| |
|Lu = 0 in G <==> u(A)+ u(B) = u(C)+ u(D) f¨ur jedes charakteristische Parallelogramm (ABCD), das in|
|G liegt. |
| |
-----------------------------------------------------------------------------------------

Nachweis:

„“ folgt aus Satz 1. „“ zeigen wir folgendermaßen. Wir nehmen an, daß es ein (x₀,t₀) mit Lu(x₀,t₀) > 0.

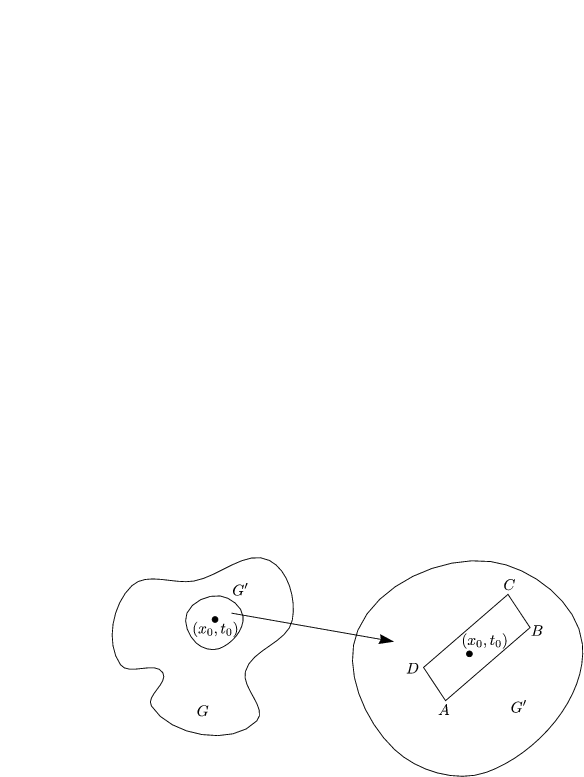
Da Lu stetig ist in G, gibt es ein G' G, (x₀,t₀ G' mit Lu(x,t) > 0. Wähle das charakteristische Parallelogramm (ABCD) G' mit (x₀,t₀) (ABCD). Nach Satz 1 gilt:

integral integral 0 < Lu d(x,t) = 0 (ABCD)

Dies stellt also ein Widerspruch dar.

Übung:

Entwickle u(x₀,t₀ - h) - u(x₀,t₀) mit dem Satz von Taylor bis zur 2.Ordnung und lassen h gegen Null gehen.

Nochmalige Herleitung der D'ALEMBERTschen Formel:

Es soll folgendes Anfangswertproblem gelöst werden:

2 utt- cuxx = f(x,t) mit x (- R, t > 0

u(x,0) = f(x), ut(x,0) = Y(x) f¨ur x (- R (*)

Gesucht ist u(x₀,t₀).

integral integral integral integral Lu(x,t)d(x,t) = f(x,t)dt = /_\ (ABC) /_\ (ABC) integral B( ) integral C( ) integral A( ) = -utdx - c2uxdt + -ut dx- c2uxdt + - utdx- c2uxdt = A B C x0 integral +ct0 = -Y(x) dx+ c(u(x0,t0)- u(x0 + ct0,0))- c (u(x0- ct0,0)- u(x0,t0)) x-ct0

(2.3)

|-----------------------------------------------------------------------------| | t integral 0 x0+c integral (t0-t) x0 integral +ct0 | u(x0,t0) =-1 f(x,t)dxdt+ -1 Y(x)dx + 1(f(x0- ct0)+ f(x0 + ct0)) | 2c 2c 2 | ------------t=0x=x0--c(t0- t)-------------x0-ct0-----------------------------------

Satz 3:

$|----------------------------------------------------------------------------------------| | | | | | 1.) Gen¨ugt u dem Problem (*), so hat u die obige Darstellung (D'ALEMBERTsche Formel). | | 2.) Sind f (- C2(R), Y (- C1(R) und f (- C1(R × (t > 0)), so u gema¨ß der D'ALEMBERTschen Formel | in C2(R × (t > 0)) /~\ C1 (R × (t > 0)). | | | -----------------------------------------------------------------------------------------$

Beispiel:

utt- c2uxx = x2 mit t > 0 und x (- R

u(x,0) = x f¨ur x (- R

u(x,0) = 0 f¨ur x (- R t

1.Schritt:
Wir suchen zuerst eine stationäre Lösung:
$u = u (x) = --1--x4 1 1 12c2$
2.Schritt:
Wir machen einen Ansatz für die gesuchte Funktion u(x,t):
$u(x,t) = u1(x)+ w(x,t)$
Für w erhalten wir dann folgendes homogenes Problem:
$2 wtt- cwxx = 0$

$w(x,0) = x +-1--x4, wt(x,0) = 0 12c2$
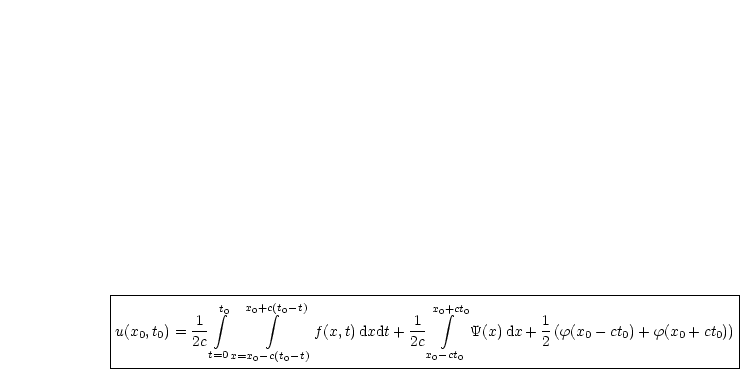
Dieses Problem ist nun einfach mit der D'ALEMBERTschen Formel zu lösen:
$|--------------------------------| | 1 | w(x,t) =-2-[w(x--ct,0)-+w(x-+-ct,0)]$

[next] [front] [up]