3.1 Kugelkoordinaten

Wir benutzen die Größen r, , :

x1 = rcosf sin h

x2 = r sinf sinh

x3 = r cosh

Dies gilt für 0 < < r, 0 < < und 0 < < 2.

(cos f sinh) sin fsinh x = x(r,h,f) = r cosh

Mittels der Funktionaldeterminante berechnen wir das Volumenelement:

det(xr,xh,xf) = r2sinh

Also gilt für das Volumenelement:

dt = r2sinhd(r,h,f)

Das Oberflächenelement kann mittels Kreuzprodukt berechnet werden:

ds = ||xh× xf|| d(h,f)

2 2 ds = r sinhd(h,f) = r dw mit dw = sin hd(h,f)

Der Normaleneinheitsvektor ist dann gegeben durch:

(cos fsin h) sinf sin h n(h,f) = cosh

Wir integrieren in Kugelkoordinaten:

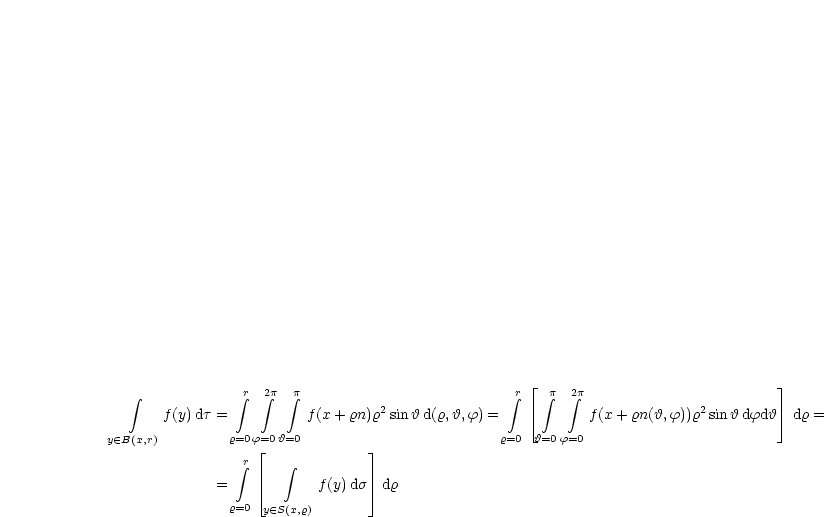|_ _| integral integral r 2 integral p integral p integral r integral p integral 2p f (y)dt = f (x + rn)r2sinh d(r,h,f) = |_ f(x+ rn(h,f))r2sinh dfdh _| dr = y (- B(x,r) r=0 f=0h=0 r=0 h=0f=0 r |_ _| integral integral = |_ f(y)ds _| dr r=0 y (- S(x,r)

(3.1)

Des weiteren gilt:

integral integral integral f(y)ds = r2 f(y)dw = r2 f(x + rn)dw |y-x|=r |y-x|=1 ||n||=1