3.2 Sphrisches Mittel der Funktion h = h(y) <img src="cmsy10-32.gif" alt=" (- " class="10x-x-32" width="8" height="9" /> C0(<img src="msbm10-52.gif" alt="R" class="10x-x-52" width="11" height="11" />3)

3.2 Sphärisches Mittel der Funktion h = h(y) C⁰(³)

Über S(x,r) bilden wir den Mittelwert von h über der Oberfläche:

integral integral Mh(r;x) = -1-- h(y) ds = 1-- h(x+ rn)dw 4pr2 4p S(x,r) ||n|| =1

Darüber hinaus können wir das sphärische Mittel einer zeitabhängigen Funktion h definieren:

integral 1-- Mh(r,t;x) = 4p h(x+ rn,t)dw ||n|| =1

Aus h C^k(³ ×{t > 0}) folgt M_h C^k(³ × (t > 0)).

1 integral Mh(0, t;x) = 4p- h(x,t)dw = h(x,t) ||n||=1

Problem:

Gesucht ist u C²(³ × (t > 0)) $/~\$ C¹(³ × (t > 0)) mit u_tt(y,t) - c² $/_\$ ₃u(y,t) = 0, y ³, t > 0.

u(y,0) = f(y), ut(y,0) = y(y) mit y (- R3

1.Schritt:
Wir nehmen an, daß das Problem lösbar ist. Es sei u = u(y,t) gegeben und x ³, t > 0 beliebig. Integriere die Gleichung über B(x,t):
$integral integral integral ( ) utt(y,t)dt(y) = c2 /_\ 3u(y,t)dt(y) = c2 \~/ . \~/ u (y,t)dt(y) |y- x|<r |y-x|<r |y-x|<r$

$integral integral \~/ .w dt = w .nds G @G$
Mit dem Gaußschen Integralsatz folgt dann:
$integral ( ) integral I = c2 \~/ . \~/ u (y,t) dt(y) = c2 \~/ u(y,t).nyds = ||y- x|| <r ||y-x||=r integral 4p integral = c2r2 \~/ u(x-+-rn,t).n(x-+-rn)dw = c2r2@r4p u(x+ rn,t)dw = ||n||=1 @ru(x+rn,t) ||n||=1 2 2 = c r .4p .@rMh(r, t;x)$ (3.2)

Wir notieren uns nochmals die Wellengleichung:

u_tt(y,t) - c² $/_\$ ₃u(y,t) = 0 für y ³, t > 0
u(y,0) = (y)
u_t(y,0) = (y)

Außerdem hatten wir das sphärische Mittel eingeführt:

integral h = h(x) : M (r;x) =-1 h(y)ds h 4pr2 ||y-x||=r

1 integral h = h(x,t) : Mh(r,t;x) = 4pr2 h(y,t)ds ||y-s||=r

u genüge (1), (2), (3). (x,t) ³ × (t > 0) sei beliebig und fest. $integral @ utt(y,t)dt(y) = 4pc2r2-Mu(r,t;x) ||y-x||<r @r$

$|_ _| integral integral integral r integral utt(y,t)dt = @2t u(y,t)dt = @2t |_ u(y,t)ds _| dr = ||y-s|| <r ||y-x||<r r=0 ||y-x||=r r |_ _| r | _ _ | 2 integral 2 integral 2 integral 2 1 integral = @t r |_ u(x+ rn,t)dw _| dr = 4p@t r . 4p |_ u(x +rn,t)ddw _| dr = r=0 ||n|| =1 r=0 ||n||=1 integral r = 4p@2t r2Mu(r,t;x)dr r=0$ (3.3)

Damit erhalten wir:
$|-- integral ------------------------------------- integral r---------------| | u (y,t)dt = 4pc2r2@ M (r,t;x) = 4p r2@2M (r,t;x)dr| | tt (y) r u t u | -||y-x||<r----------------------------------r=0-----------------$

$integral r 2 2 2 2 c r @rMu(r, t;x) = r @tMu(r, t;x) dr r=0$
Durch partielles Differenzieren nach r fällt das Integral weg:
$c2 [2r@rMu(r,t;x)+ r2@2rMu(r,t;x)]= r2@2tMu(r,t;x)$
Es kann noch durch r0 dividiert werden:
$2[ 2 ] 2 c 2@rMu(r,t;x) + r@rMu(r, t;x) = r@tMu(r,t;x)$
Wir setzen M_u(r,t;x) := und formen den Ausdruck geschickt um:
$c2(c'+ c'+ rc'') = c2(c'+ (rc')') = (c + rc')'= ((rc)')'$
Damit erhalten wir also:
$2 2 2 c @r [rMu(r,t;x)] = @t [rMu(r,t;x)]$
Wir führen eine neue Variable ein, nämlich U(r,t;x) := rM_u(r,t;x) und schreiben damit die Gleichung:
$|------------------------------------| |(Utt- c2Urr)(r,t) = 0 f¨ur r > 0 und t > 0 -------------------------------------$
Wir wissen, daß U(0,t) = 0 für t > 0 gilt.
$integral integral U (r,0) = r .1-. u(x + rn,0)dw = r-. f(x +rn) dw = rMf(r; x) 4p 4p ||n||=1 ||n|| =1$
Analog folgt:
$Ut(r,0) = r.My(r; x)$
Also schreiben wir uns nochmals das Problem für U(r,t) = rM_u(r,t;x) hin:
$Utt -c2Urr = 0 f¨ur r > 0 und t > 0$

$U (r,0) = rMf(r; x)$

$Ut(r,0) = rMy(r; x)$

$U(0,t) = 0$
Wir erinnern uns nochmals an das sphärische Mittel:
$integral M (r,t;x) =-1- u(x+ rn,t)dw u 4p ||n||=1$

$Mu(0, t;x) = u(x,t)$

$@rU (r,t) = Mu(r,t;x)+ r@rMu(r,t;x)$

$@rU (r,t)| r=0 = u(x,t)$

Für r > ct bekommen wir die Lösung einfach durch Anwendung der D'ALEMBERTschen Formel:
$r+ integral ct U(r,t) = 1[(r + ct)Mf(r + ct,x)+ (r- ct)Mf(r - ct;x)]+ 1- sMy(s;x)ds 2 2c r-ct$
Für 0 < r < ct gilt dann:
$1 1 ct integral +r U(r,t) = 2 [(r + ct)Mf(r + ct;x)- (ct- r)Mf(ct- r;x)]+ 2c sMy(s;x)ds ct- r$
Außerdem gilt durch Differentiation nach r und Einsetzen von r = 0:
$1 1 @rU(r,t)| r=0 = 2 [Mf(ct;x)+ ct@rMf(ct;x)+ Mf(ct;x)+ ct@rMf(ct;x)]+ 2c-[ctMy(ct;x)+ ctMy(ct;x)]$

$u(x,t) = Mf(ct;x) + ct@rMf(ct;x)+tMy(ct;x) -----@-(tM-(ct;x))------ t f$
Unser 1.Ergebnis ist nun:
Ist u Lösung des CAUCHY-Problems (1), (2), (3) im ³, so gilt:
$u(x,t) = @t(tMf(ct;x))+ tMy(ct;x)$
Ist C³, C², so ist durch (L)u(x,t) := _t(tM(ct;x) + tM(ct;x) mit x ³, t > 0 eine Lösung des CAUCHY-Problems (1), (2), (3) gegeben.
Es sei h C² und u_h(x,t) := tM_h(ct;x). Es gelten:
$2 (uh)tt- c /_\ uh(x,t) = 0 f¨ur x (- R und t > 0$

$uh(x,0) = 0, (uh)t(x,0) = h(x)$
Daraus folgt die obige Behauptung. (L) lautet nun folgendermaßen:
$u(x,t) = @tuf(x,t)+ uy(x,t)$
Zu zeigen ist, daß _t² - c² $/_\$ = 0 ist. Außerdem muß gelten:
$@tuf(x,0) = f(x)$

$@t(@tuf)(x,0) = 0$

$[ 2 ] 2 (uf)tt- c /_\ uf t = 0 = ((uf)t)ttc /_\ (uf)t$
Mit u(x,0) = 0 erhalten wir dann außerdem:
$(@2tuf)(x,0) = c2 /_\ uf(x,0) = 0$

$t integral uh(x,t) =--- h(x + ctn) dw (- C2 4p||n||=1$

$(uh)t(x,0) = Mh(0; x)+ t@t Mh(ct,x)| t=0 = h(x)$

$integral uh(x,t) ct- (uh)t(x,t) = t + 4p \~/ h(x +ctn).n dw ||n||=1$
Mittels Satz 1 und dem Gaußschen Satz resultiert dann:
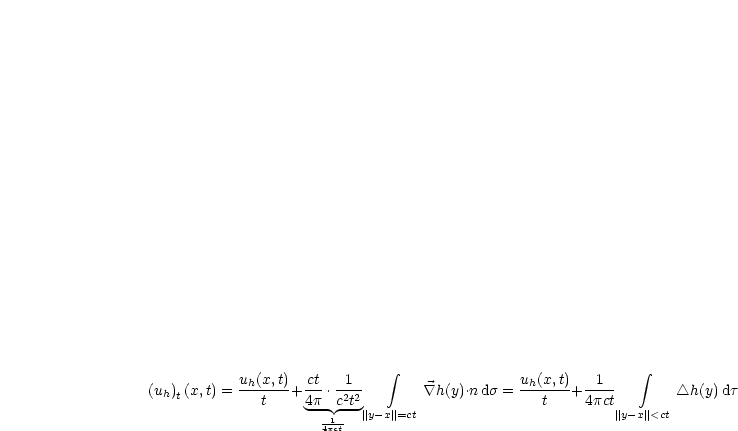
$integral integral uh(x,t)- ct- -1-- uh(x,t) --1- (uh)t(x,t) = t + 4p-.c2t2- \~/ h(y).nds = t +4pct /_\ h(y)dt -1- ||y-x||=ct ||y-x|| <ct 4pct$

$|_ _| integral integral (uh) (x,t) = - 1-uh(x,t)+ 1(uh) (x,t)--1--- /_\ h(y) dt+-1-@t |_ /_\ h(y)dt _| tt t2 t t 4pct2 4pct ||y-x<ct ||y-x||<ct$
Wir setzen den Ausdruck für _t(x,t) aus der ersten Gleichung in die zweite Gleichung ein:
$|_ _| |_ ct _| 1 integral 1 integral 2 integral (uh)tt(x,t) = 4pct@t |_ /_\ h(y)dt _| = 4pct@t |_ r /_\ h(x + rn)dw _| dr = ||y-x||<ct r=0 ||n||=1 c 22 integral 2 t integral 2 = 4pct-.ct . /_\ h(x + ctn)dw = c .4p-. /_\ h(x + ctn)dw = c /_\ uh(x,t) ||n|| =1 ||n||=1$ (3.4)

$integral u (x,t) = t-- h(x+ ctn)dw h 4p ||n|| =1$

|_ _| 1 integral 1 integral u(x,t) = @t(tMf(ct;x))+ tMy(ct;x) = @t |_ 4pc2t f(y)dt(y) _| + 4pc2t- y(y)ds = ||x-y||=ct ||y-x||=ct 1 integral [ ] 1 integral [ ] = 4p- f(x +ctn)+ \~/ f(x + ctn).cn dw + ...= 4pc2t2 f(y)+ \~/ f(y) .(y- x) ds = ||n|| =1 ||y-x||=ct 1 integral [ ] = 4pc2t2- f(y)+ \~/ f(y).(y - x)+ ty(y) ds ||y-x||=ct

(3.5)

Bemerkung:

Für n = 3 ist im allgemeinen die Lösung weniger regulär als die Anfangsdaten (wegen $\~/$ in der Lösung).
Das CAUCHY-Problem hängt im folgenden Sinn stetig von den Anfangsbedingungen ab. Aus a_k, $\~/$ _k $\ ~/$ , _k folgt dann u_ku für k. $[]uk = 0$

$uk = fk f¨ur t = 0$

$ukt = yk f¨ur t = 0$
Also gilt:
$[]u = 0, u = f, ut = y$