3.3 Cauchy-Problem fr n = 2/Absteigemethode (Method of descend)

Gesucht ist ein u C²(² × (t > 0)) $/~\$ C¹(² × (t > 0)). Mit ₂u(x,t) = u_tt - c² = 0 mit u(x,0) = (x) und u_t(x,0) = (x) bei x = (x₁,x₂) ², t > 0.

3 2 2 2 f (- C (R ), y (- C (R )

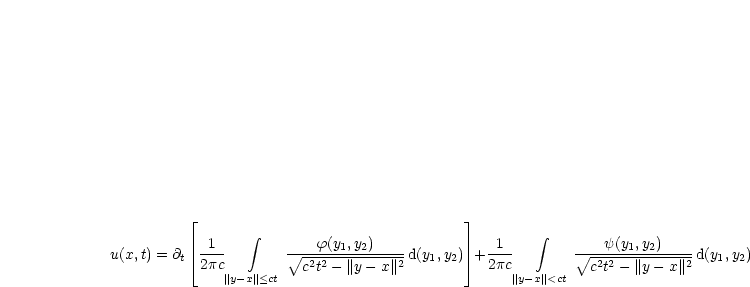
Betrachte das Problem formal als dreidimensionales Problem, das von x3 unabhängig ist. u = u(x₁,x₂,x₃,t) genüge folgendem Problem:

2 3 utt- c (ux1x1- ux2x2) = 0, (x1,x2,x3) (- R , t > 0

-- u(x1,x2,x3,0) = f(x1,x2,x3) := f(x1,x2)

-- ut(x1,x2,x3,0) = y(x1,x2,x3) := y(x1,x2)

u ist bekannt und daraus ergibt sich u(x,t) = u(x₁,x₂,0,t) mit x := (x₁,x₂,0).

---- -- -- u(x,t) = u(x,t) = @t(tMf(ct;x))+ tMy(ct;x) = |_ integral _| -1--- -- = @t |_ 4pc2t f(y1,y2,y3)ds(y1,y2,y3) _| +analog = || integral (y1,y2,y3)-(x1,x2,0)||=ct = f(y1,y2)ds(y1,y2,y3) ||(y1,y2,y3)- (x1,x2,0)|| =ct

(3.6)

Wir schreiben die Kugelfläche in Parameterdarstellung an:

(y1- x1)2 + (y2- x2)2 + y32= c2t2

V~ ------------- y3 = ± c2t2 - ||y- x||2,||y- x||2 < c2t2

( ) y1 r(y1,y2) = y2 y3(y1,y2)

------ct------- ds = ||ry1× ry2||d(y1,y2) = V~ c2t2--||y--x||2 d(y1,y2)

Wir erhalten als Ergebnis:

|_ _| integral integral u(x,t) = @t |_ -1 V~ --f(y1,y2)----d(y1,y2) _| +-1- V~ --y(y1,y2)----d(y1,y2) 2pc||y-x||<ct c2t2- ||y - x||2 2pc||y-x||<ct c2t2- ||y - x||2