3.6 Die Wellengleichung in beschrnkten Raumgebieten (Entwicklung nach Eigenfunktionen des -<img src="cmsy10-34.gif" alt=" /_\ " class="10x-x-34" width="12" height="11" />-Operators

3.6 Die Wellengleichung in beschränkten Raumgebieten (Entwicklung nach Eigenfunktionen des - $/_\$ -Operators

G ³ sei ein beschränktes Gebiet mit G = G G. G sei stückweise glatt. Gesucht sei u = u(x,t), definiert für x G, t > 0. Wir haben also das Problem:

(utt- c2 /_\ 3u)(x, t) = 0 f¨ur x (- G, t > 0

u(x,0) = f(x), ut(x,0) = y(x) f¨ur x (- G

u(x,t) = 0 f¨ur x (- @G und t > 0

Wir machen einen Separationsansatz. Dies kann man bei beschränkten Gebieten immer versuchen!

u(x,t) = v(x)T(t)

Wir setzen diesen Ansatz in die obige Gleichung ein und erhalten:

'' 2 2 T v -c T /_\ v = 0 | : (c .vT )

1 T''(t) Dv c2-T-(t)-= -v-(x) = - c

sei der Separationsparameter. Wir erhalten also zwei gewöhnliche Differentialgleichungen:

T ''(t)+ cc2T(t) = 0

/_\ v(x)+ cv(x) = 0, v(x) = 0 f¨ur x (- @G

Zu betrachten ist das Eigenwertproblem - $/_\$ v(x) = v(x) (x G), v(x) = 0 (x G). Gesucht sind Lösungen v0 und zugehörige ’s, also gerade die Eigenwerte.

Jeder Eigenwert ist positiv. $- /_\ v = cv in G$
Wir multiplizieren nun mit v(x) durch und integrieren:
$integral integral - 2 - /_\ v(x)v(x) = c |v(x)| G G$

$integral integral | \~/ v |2dx= c |v(x)|2dx G--- --- -G--- ----- >0 >0$
Daraus folgt dann = 0 oder > 0. = 0 bedeutet:
$integral 2 | \~/ v| dx = 0 G$
Damit erhalten wir schrittweise:
$\~/ v = 0 in G$

$-- v = const.inG$
Aus v_G = 0 folgt dann v = 0 und dies ist nach Definition keine Eigenfunktion.
Übung:

Mit v als Eigenfunktion zu ist auch v Eigenfunktion zu .
v₁ sei Eigenfunktion zum Eigenwert ₁. v₂ sei Eigenfunktion zu ₂ und es gelte ₁₂, dann gilt v₁ v₂. $integral v1(x)v2(x)dx = 0 G$
Wir rechnen dies nach:
$- /_\ v1 = c1v1$

$- /_\ v2 = c2v2$
Es sei ₁₂.
$integral integral (c1- c2) v1(x)v2(x) d(x) = [v1 /_\ v2 - v2 /_\ v1] dx G G$

$integral [ ( ) ( ) ] integral [ ] \~/ . v1 \~/ v2 - \~/ . v2 \~/ v1 - \~/ v1 . \~/ v2 + \~/ v2 . \~/ v1 dx = v1 \~/ v2 - v2 \~/ v1 nds G @G$
Es gibt abzählbar viele Eigenwerte ₁, ₂, ₃, ... mit 0 < ₁ < ₂ < ₃ < ... < _n < _n+1 < ... mit _n für n.
Zu jedem Eigenwert gibt es höchstens endlich viele Eigenfunktionen (endliche Vielfachheit).
Jede Eigenfunktion v gehört zu C₁(G).

3.6.1 Entwicklungssatz

|------------------------------------------------------|
| -- |
|Es sei f (- C2(G) und f (x) = 0 f¨ur x (- @G. Dann gilt: |
| |
| sum oo -- |
|f(x) = akvk(x) f¨ur x (- G |
| k=1 |
| -- |
|Die Konvergenz ist gleichma¨ßig (also unabh¨angig von x) auf G.
--------------------------------------------------------

Man hat dann:

integral f(x)v (x)dx k ak = G- integral ---------f¨ur k = 1, 2, 3, ... v2k(x)dx G

Ergebnis:

Sind , in G genügend oft stetig differenzierbar, so ist die Lösung des Anfangswert-Randwertproblems (1), (2), (3) durch die Reihe

|------------------------------------------------------| | oo sum [ ( V~ ---) (y,v ) ( V~ --)] | |u(x,t) = (f,vn)cos c cnt + - V~ -n-sin c cnt vn(x)| ---------n=1--------------------c--cn------------------

gegeben, wobei (•,•) für zwei reellwertige Funktionen f und g folgendermaßen definiert ist:

integral (f,g) = f(x)g(x)dx G

Beispiel:

Ist G = {(x,y) ²|0 < x < a, 0 < y < b} ein Rechteck, so wird das Eigenwertproblem (4)

-vxx- vyy = cv(x,y) mit (x,y) (- G, v(0,y) = v(a,y) = v(x,0) = v(x,b) = 0

wieder mit einem Separationsansatz v(x,y) = X(x)Y (y) gelöst. Man erhält die orthonormierten Eigenfunktionen

( ) ( ) vnm(x,y) = V~ 2-sin np-x sin mp-y f¨ur n, m = 1, 2, 3, ... ab a b

mit den Eigenwerten

(np )2 (mp )2 cnm = --- + --- a b

Beispiel:

Ist G = {(x,y) |x² + y² < R²} ein Kreisgebiet, so wird (1), (2), (3) mit Polarkoordinaten geschrieben (u(r cos,r sin,t) := w(r,,t)):

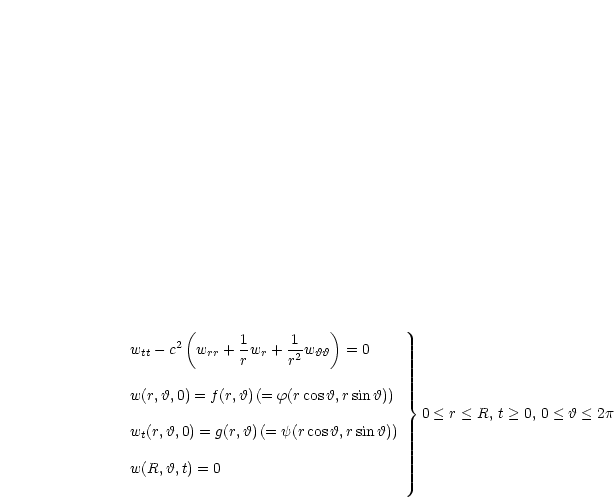
( ) w - c2 w + 1w + 1-w = 0 tt rr r r r2 hh w(r,h,0) = f(r,h)(= f(rcosh,rsin h)) } 0 < r < R, t > 0, 0 < h < 2p wt(r,h,0) = g(r,h)(= y(rcosh,r sinh)) w(R, h,t) = 0

Der Separationsansatz w(r,,t) = (r,)(t) mit (r,) = $/\$ (r)() liefert für $/\$ (r) eine BESSELsche Differentialgleichung mit Parameter n von der eine im Nullpunkt reguläre Lösung gesucht wird. Bei der Gleichung für ist zu beachten, daß eine 2-periodische Lösung = (r) gefordert ist.

[prev] [prev-tail] [front] [up]

3.6 Die Wellengleichung in beschränkten Raumgebieten (Entwicklung nach Eigenfunktionen des --Operators

Übung:

3.6.1 Entwicklungssatz

Ergebnis:

Beispiel:

Beispiel:

3.6 Die Wellengleichung in beschränkten Raumgebieten (Entwicklung nach Eigenfunktionen des - $/_\$ -Operators